Quadratic Equation (Part 2)

Applying The Quadratic Formula To Solving Quadratic Equation
The Quadratic Formula is one of the most easiest and convenient method of solving Quadratic Equation. I derived the Quadratic Formula and I explained alot about it which you can find here Quadratic Equation Part 1. Today we gonna consider how we can can solve Quadratic Equation by using formula method. I will take you through series of examples which will make you comprehend the and understand the topic easily.
Example 1
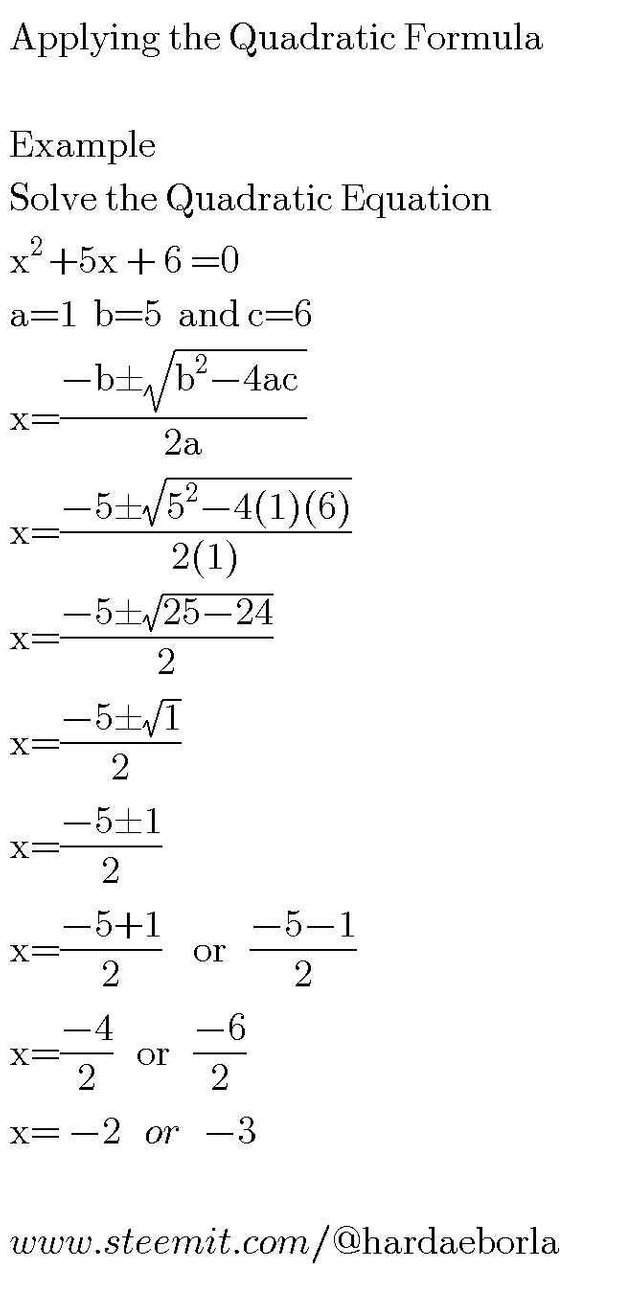
From the above Example, we were told to determine the value of x. By mere inspection, we should know we are to get two values for x because every Quadratic Equation will always yield two solutions.
Let's Scrutinize the above question with care😁
x² +5x +6=0
Firstly, we consider the coefficient of the variables.
What do we mean by coefficient?
Coefficient is any value preceding the variables. They are usually anything you find in front of a variable. For Example, the coefficient of x in 5x is "5" because that's what comes before x. Similarly, the coefficient of x² in the equation 5x³ +4x² +9=0 is "4" because that's the number before x². Anytime we consider coefficient, we neglect other variables except the variable we need. That's just by the way 😀. Let's get back to business 😁. Anytime you solve Quadratic Equation using Quadratic Formula, the coefficient are only considered.
Analysing Example 1
x² +5x +6 =0
- The coefficient of x² is 1 which is equal to "a"
- The coefficient of x is 5 which is equal to "b"
- The coefficient of x^0 is 6 which is also known as a constant is given by "c".
Are you surprised that every constant is also subjected to a variable? Yes, they are always next to a variable which is always in power 0. In Standard Mathematics, we call the coefficient constants and ignore the variable because one of the laws of indices proposes that anything raise to power 0 is always 1 except 0 power 0.
Thus, a^0=1, where a≠0. This implies a can be any value but it must never be 0 has this will yield to an undefined solution.
After knowing the coefficient which are
- a=1
- b= 5
- c =6
We now substitute it into the Quadratic Formula which is x=-b±√(b²-4ac)/2a. This means anywhere you see "a" in the formula you input "1" , anywhere you see "b" in the formula you input "5" and anywhere you see "c" in the formula you input "6". Then you can get the value of x from the above image.
Let's Consider Another Example
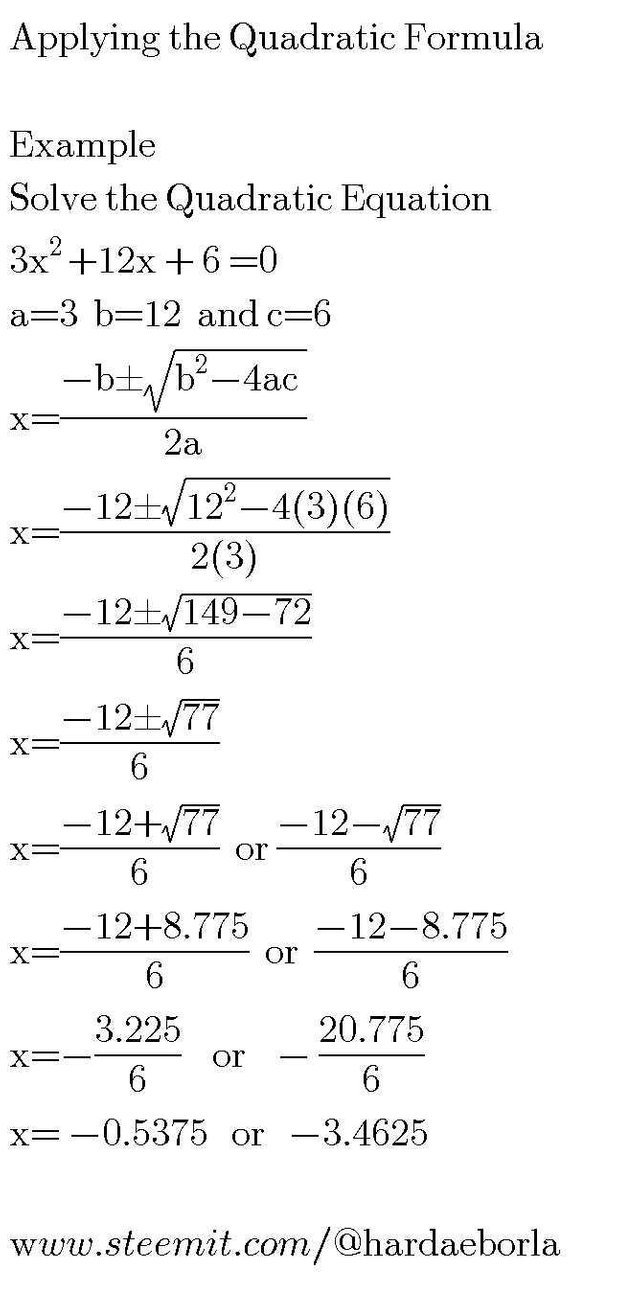
As you can see it's almost the same step just like the first example, the only difference is the coefficient of x². We can notice that the coefficient of x² isn't "1" in this case, the coefficient of x² is 3. This means
- a=3
- b=12
- c=6
After knowing the values of a, b and c then we substitute those values into the Quadratic Formula and we get the two values of x. In the above solution, we observe x to be two negative values with rational numbers. Thus, don't be surprised about this because I have explained more of such cases in Solutions of Quadratic Equation. Always know that you are expected to get "two values after solving Quadratic Equation With the Quadratic Formula".
You Have the chance of winning SBD by Solving this Tutorial Question on Quadratic Equation
To Win my free SBD, just follow this 3 steps
- Upvote
- Resteem
- Show your workings and answers by commenting after reading the tutorial question
IT'S QUIZ TIME 😀🙌

Question 1
Solve the Quadratic Equation using Formula method
Question 2
Solve the Quadratic Equation using Formula Method
Good luck and feel free to ask questions you don't understand.
Solid post.
Namaste, JaiChai
Namaste 💗
Well explanatory.keep it up
Thanks bro. Feel free to take part in in quiz
Hai...dont mistake me..I am in steemit for the last 9 months and almost daily I comes here but never seen such an educational post...Good one..hope it may useful to some people...
@angelro... Thank you for your wonderful comment. 💗🙌