How mathematics help us discover the REAL transcendent world (according to Plato)

Eternity and nothing cannot be understood trough mathematics.
But perhaps can anything else?

Mathematics becomes part of the topics in several of Plato’s dialogues. The ancient Greeks used mathematics in their everyday life, and in crafts that benefitted from it. Pythagoras (approximately 580-500 BC) laid down the fundament for the practice and philosophy of mathematics in Athens during Plato’s time with discoveries in geometry (Pythagoras’ theorem) and with his notion that all the small particles as well as huge objects (like stars, planets) in the universe operates in harmony with each other in mathematical relations (Pythagorean notion of Harmony, as I will call it in this article). In Plato’s Republic, mathematics has the role as an important part of the education of the citizens in Socrates’ ideal city, some of them to become the future philosopher kings. According to Republic VII, mathematics will help turn the soul towards the study of being.

Mathematics and mathematical education

Mathematical entities are abstractions of the visible objects around us and relations between them. These entities are crucial in the intelligible realm, where invisible connections and causes can be seen by an “instrument (of the soul) more important than ten thousand eyes”. After reading what Socrates says about mathematical abstractions in the Republic, I understand mathematical entities as real things, more real than everyday things coming to be and coming to end. Understanding Plato as a dualist, who takes the soul to be of something else than what we find in the physical world, somehow three-dimensional, but not extended in space, the thought that mathematics as existing apart from the physical world fits the soul better than these things we see around us comes quite naturally. They belong to the idea level, which for Plato is a higher level than the things we experience through our senses belongs to:

It leads the soul forcibly upward and compels it to discuss the numbers themselves, never permitting anyone to propose for discussion numbers attached to visible or tangible bodies. (S. M. Cohen et al., 2011, p. 552)

The plan with this education is to educate the future philosopher kings in theoretical mathematics so they better will gain knowledge of pure forms and use this for the best possible leadership of the city state. Education in mathematics comes after poetry, music and physical training and will last for ten years in the ideal city. The order of mathematic disciplines that Socrates propose begins with arithmetic, because it gives insight into mathematical entities as such, making understanding of numbers themselves possible. After arithmetic comes plane geometry, then stereometry. Stereometry is at the time discussed not very well developed, but seems to have importance in light of understanding the underlying principles of objects in three dimensions. After these comes astronomy. Astronomy is important in this education, not as the study of visible objects in the sky as visible moving objects, but as the study of the movements and patterns in a mathematical way, invisible properties and being of these objects and the harmony they are part of. Harmonics is the discipline most relevant to the subject of the Republic as a whole, namely the adjustment of the soul to make it just. It is also very tight connected with the understanding of astronomy, music and the tasks that awaits the future rulers of the ideal republic, such as social structures, law and justice.

Mathematics’ relation to Plato’s forms and image of the Line

Mathematics are important for the soul to be able to grasp the higher reality of forms. Plato sets pure forms equal to understanding in his image of the line, and they are one level higher than mathematical entities in Plato’s line. Mathematical entities equal reasoning, and reasoning is necessary to reach the next level of knowledge. The thorough education in mathematics are somehow a preparation for the next level of education towards the best possible understanding, which is dialectics, as dialectics need a fundament of arithmetic, geometric and astronomical knowledge to be used properly. What is important to mention about these forms, is that they don’t have extension. They are not visible, they cannot be touched or heard, but only through our intellect, through the valuable instrument in our soul, can the forms be understood. The image of the line is divided into four levels. Imagination is at the bottom, as the lowest level of knowledge possible. Belief is superior to imagination, but both are labelled opinion by Plato. Reasoning and understanding are labelled as intellect, and superior to opinion. Understanding is here the highest possible form of knowledge and equals Plato’s eternal forms.

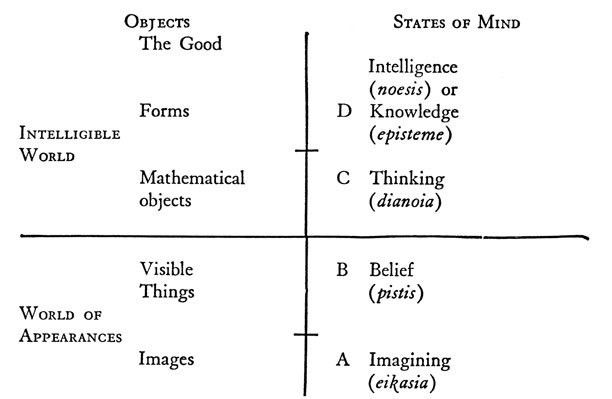
The distinction between being and becoming is crucial to understand Plato’s view on mathematics and the forms. The world of becoming is the everyday physical, empirical world that we see around us. This world is less true than the ideal world Plato wants us to grasp. The world of being is the realm of the Forms. The study of being is the study of what always is, no matter what, the very structures beyond the things that comes to be and passes away. Forms exists, according to Plato, although not in the way physical things do. Things in the physical world resembles these forms, and through reasoning about the nature of these we can gain knowledge of the forms themselves.

Some things are easily judged by its appearance, with help of the sight only. Other things open up for some investigation into the thing being that thing, of its causes, features and relation to other things alike and unlike it. The philosophical mind will search beyond the mere sensible impression of the thing, for some underlying principles that will reveal another kind of knowledge of the thing itself and perhaps of other things. In Republic VII Socrates argues that education in mathematics is needed if one is to discover and make use of these principles. Eternity and nothing cannot be understood trough mathematics. But perhaps can anything else? Mathematics are important for education of the soul in the way it makes the invisible underlying principles of the universe graspable in some cases. Plato seems to presuppose that numbers are real things regardless of human activity, they are eternal, nontemporal, nonphysical things.

Harmony and concordance

Harmony was important to the ancient Greeks, and not only in music, where we find the term harmony most commonly used today. Harmony is what unifies a whole, making it one and not several lesser parts. In the mathematical sense, harmony is numbers in accordance to each other, as 1:2, 2:3, 3:4. These ratios will give a harmonic sounding chord when played on strings equally tuned. This kind of harmonic concordance between mathematical numbers, according to Pythagoreans and other ancient Greek mathematicians and philosophers, is not only present in the mathematical structure of pleasing sounds, but present in the structure of the cosmos itself. Harmony is what unifies, in opposition to discordance. Adding discording numbers produces something distorted and not unified. How does this relate to the claim that mathematics is good for the soul, and what does Socrates mean about this with regards to educating the future rulers of the ideal city?

Then, if each is one, and both two, the soul will understand that the two are separate, for it wouldn’t understand the inseparable to be two, but rather one. (S. M. Cohen et al., 2011, p. 551)

As harmony between parts of a unity makes that unity a balanced, good unity, and this is not assigned to particular unities, but unity itself, the unity that is the soul should also be harmonic. For a soul to be just it seems necessary that the soul’s faculties must be harmonic balanced with each other, just as the three faculties of the ideal city must be to be just. Therefore, understanding the mathematical relations and the numbers themselves makes the subject better aware of that unity the subject itself is, and hence its own being. This way the subject can know whether it is just or not, as well as judge other things as just or not in the light of harmonic unity understood through mathematics.

In the article From Music to Physics: The Undervalued Legacy of Pythagoras, Caleon and Ramanathan writes:
Pythagoras and the Pythagoreans, went much further, relating their notion of musical harmony to the order in the structure of the cosmos, believing that the arrangement of planets follows a musical progression, with the ratio of their distances also expressible in simple whole numbers” (I. Caleon & S. Ramanathan, p. 450)
The Pythagoreans had introduced a valuable idea that is central to the development of the scientific enterprise: all complex phenomena must reduce to simple ones. They were able to forge a marriage between music and mathematics, a link that they extended to the structure and working principles of the universe. (I. Caleon & S. Ramanathan, p. 455)
The Pythagorean view is very much present in Plato’s writings. It is the same principles behind what is good, what is true, and what is beautiful. There is balance, concordance and unity in these things, and they were believed to share “beautiful” ratios in numbers. By understanding the recipe behind harmonic things, we become closer to understanding the Good itself, because the Good itself is resembled in such things. Mathematics also helps tune the Soul so it becomes harmonic, and in that it becomes just. The parts of the soul, if they are tuned in harmonic relation to each other, will act as a unity, like sounds in harmonic relationship with each other will be heard as one, beautiful sound, a tuned chord. This is important in the education of just men, as the Republic’s first principle is to establish some precedence on justice itself and what it is to be just.

The goal of education in Plato’s theoretical mathematics

Now that I have gained a better (and hopefully satisfying) understanding of mathematics in the time of Plato, Plato’s forms and image of the line, and harmony in the sense of an interweaving of different accounts into a single narrative[https://www.merriam-webster.com/dictionary/harmony], I will now explain in detail how mathematics help turn the soul towards the study of being (5.1) and then what changes to mathematics as previously practised Socrates recommends for it to do this job (5.2).

I have mentioned the instrument in the soul that Socrates describes are more important than ten thousand eyes. This instrument is the one that can take on a higher understanding through mathematical reasoning, and Socrates tells Glaucon that this instrument is what turns the soul away from the study of things that comes into being and comes to an end, and towards the study of what is, and it does so through education in the sense that Plato (here through Socrates) defines it, and not by “putting knowledge into souls that lack it”:

This instrument cannot be turned around from that which is coming into being without turning the whole soul until it is able to study that which is and the brightest thing that is, namely, the one we call the good. (S. M. Cohen et al., 2011, p. 546)
To turn the soul towards the study of being then, it is by this instrument it must happen, and by doing so, turning oneself towards the higher wisdom that transcends the ordinary, gaining knowledge of true forms through theoretical mathematics for a better understanding of the invisible structures – helping turn the soul towards the study of being.

Training in arithmetic have the possibility of making the learner better at all other theoretical subjects, in the way that it exercises the brain as well as in the way calculation comes to use in several other subjects than mathematics itself. This feature is not the reason Socrates holds is the most important regarding mathematical education. It is the possibility of understanding things beyond the thing itself, to be able to grasp what numbers is by itself, when not pointing at actual things.

Socrates: Now, calculation and arithmetic are wholly concerned with numbers.
Glaucon: That’s right.
S: Then evidently they lead us towards truth.
G: Supernaturally so.
S: Then they belong, it seems, to the subjects we’re seeking. They are compulsory for warriors because of their orderly ranks and for philosophers because they have to learn to rise up out of becoming and grasp being, if they are ever to become rational. (S. M. Cohen et al., 2011, p. 552)

What changes should be made: To help turn the soul towards the study of being, mathematics should, according to Socrates, be used as a tool towards understanding the Good, the whole, what some may call God and others (as the ancient Greeks) call the World Soul. I will make a distinction between practical (PM) and theoretical (TM) mathematics, where PM is the mathematical study of what comes into being and passes away (554 b) and TM is the mathematical study of that which always is. I will argue that TM is the form of mathematics Socrates recommend as an important part of the education of the future rulers (philosopher kings) of the ideal city. Theoretical study of geometry for instance, will provide knowledge that goes beyond that which belongs to crafts as house building, farming, war, and other kinds of jobs. The knowledge he seeks for this kind of education is knowledge about pure forms, and as I understand it, this is crucial to understand relations between the city’s inhabitants, between city states, in planning the city’s infrastructure, laws and other important tasks that according to Socrates should be given the wisest people in the city (those who cannot, by their conscientiousness, leave the task of ruling to less wise people). A first principle seems to be necessary for mathematics to reach the function of this, and what we call hypothesis, (from Greek hypotithenai) to put an assumption behind the mathematical investigation, is such a principle that can help turn the soul towards the study of being itself. Mathematics as mere study of empirical observation through numbers with no such principle behind it, will not fulfil the task Socrates sets for the education of the future philosopher kings. This kind of mathematical study (PM) is far from useless, i.e. as tools used in the crafts of other citizens (merchants, farmers, producers of tools, etc.) but not sufficient in the study that will prepare the best students for the tasks that awaits the ruler(s) of the city and knowledge of pure forms. About astronomy, Socrates says: “As it’s practised today by those who teach philosophy, it makes the soul look very much downward.” (S. M. Cohen et al., 2011, p. 555) When discussing astronomy with Glaucon, Socrates compares the study of it at the present time with the practical study of music (p. 557), and, as I understand it, all other practical studies that does not aim to solve theoretical problems, only practical ones. On how to take on astronomy in the proper theoretical way, Socrates suggests:

We should consider the decorations in the sky to be the most beautiful and most exact of visible things, seeing that they’re embroidered on a visible surface. But we should consider their motions to fall far short of the true ones – motions that are really fast or slow as measured in true numbers, that trace out true geometrical figures, that are all in relation to one another, and that are the true motions of the things carried along in them. And these, of course, must be grasped by reason and thought, not by sight. (S. M. Cohen et al., 2011, p. 556)

Then if, by really taking part in astronomy, we’re to make the naturally intelligent part of the soul useful instead of useless, let’s study astronomy by means of problems, as we do in geometry, and leave the things in the sky alone. (S. M. Cohen et al., 2011 p. 556)

Mathematics should be taught for the sake of the Good, as a way to understand the highest forms which cannot be understood trough sense information alone. Those things that mathematics should “look into” are those that creates some sort of urge to investigate further into the very being of that thing, to see if there is some truth behind it which is true no matter what relation or context it finds itself in. It needs a first principle to achieve this potential. Mathematics cannot look into mathematics itself, and this is a task for dialectics, I believe. Mathematics leads to knowledge when aimed by a first principle, not on its own, therefore it is not understanding in itself, but it helps lead to it. Socrates says that mathematics should be applied to those cases where we in investigating something immediately discovers opposite measures regarding its being. This will in turn lead to the study of being itself, that which always is.

Socrates: The ones that don’t summon the understanding are all those that don’t go off into opposite perceptions at the same time. But the ones that do go off in that way I call summoners – whenever sense perception doesn’t declare one thing any more than its opposite, no matter whether the objects striking the senses is near at hand or far away. You’ll understand my meaning better if I put it this way: These, we say, are three finger – the smallest, the second, and the middle finger.
Glaucon: That’s right.
S: Assume that I’m talking about them as being seen from close by. Now, this is my question about them.
G: What?
S: It’s apparent that each of them is equally a finger, and it makes no difference in this regard whether the finger is seen to be in the middle or at either end, whether it is dark or pale, thick or thin, or anything else of that sort, for in all these cases, an ordinary soul isn’t compelled to ask the understanding what a finger is, since sight doesn’t suggest to it that a finger is at the same time the opposite of a finger.
G: No, it doesn’t.
S: Therefore, it isn’t likely that anything of that sort would summon or awaken the understanding.
G: No, it isn’t.
S: But what about the bigness and smallness of fingers? Does sight perceive them adequately? Does it make no difference to it whether the finger is in the middle or at the end? And is it the same with the sense of touch, as regards the thick and the thin, the hard and the soft? And do the other senses reveal such things clearly and adequately? Doesn’t each of them rather do the following: The sense set over the hard is, in the first place, of necessity also set over the soft, and it reports to the soul that the same thing is perceived by it to be both hard and soft?
G: That’s right.
S: And isn’t it necessary that in such cases the soul is puzzled as to what this sense means by the hard, if it indicates that the same thing is also soft, or what it means by the light and the heavy, if it indicates that the heavy is light, or the light, heavy? (S. M. Cohen et al., 2011, p. 550-551)

–––

S: If the one is adequately seen itself by itself or is so perceived by any of the other senses, then, as we were saying in the case of fingers, it wouldn’t draw the soul towards being. But if something opposite to it is always seen at the same time, so that nothing is apparently any more one than the opposite of one, then something would be needed to judge the matter. The soul would then be puzzled, would look for an answer, would stir up its understanding, and would ask what the one itself is. And so this would be among the subjects that lead the soul and turn it around towards the study of that which is. (S. M. Cohen et al., 2011, p. 552)

What does Socrates mean with summoners? Things that make our minds somehow uncertain of the nature of what we perceive, and then lights an urge to find out, dig into it and find out what this thing is beyond what we can find out about it through sense perception. I think we can call it a kind of trigger for the reasoning in our souls. It triggers the instrument that Socrates talks about, some call it the third eye, Socrates describes it as more important than ten thousand eyes. For mathematical education to do the job Socrates wants it to do regarding the turning of the soul towards the study of being, the subjects must deal with these summoners, not in themselves, but the problems that arises from the investigation of these. In this way the intellect can leave the mere physical world alone, and focus on the invisible, eternal principles earlier mentioned. Burnyeat points out a good reward from this upward directed focus when he writes:

The other side of this coin, for Plato (not Aristotle), is that someone whose soul has become assimilated to objective being can take it as a model for reorganizing the social world. (Burnyeat, 2000, p. 72)

It here becomes clear why Plato finds it necessary for the ideal city to be ruled by someone with a proper deep theoretical understanding of mathematics: being able to see the invisible structures in the world, and understanding those things that always is, makes the ruler able to see beyond what is in the terms of coming to be and coming to end, and instead into what should be.

My experience with practical and theoretical mathematics in education and why my soul are not quite yet turned towards the study of being (if I am to believe Plato)

I agree with Plato that proper theoretical mathematical education is important to be able to understand things beyond the conclusions we can make based solely on sense perceptions. The fact that the earth is a round thing is not obvious to the eye or any other sense. Only through mathematical understanding of geometry, movements and the relations between them, were humans able to conclude that i.e. the earth is a round object. We still have a lot to find out about the universe we are part of, and I am obviously convinced that looking at things and touching them is not how these new insights will be discovered. I see mathematics as a tool, a very powerful one, but am not sure whether it is a manmade tool or made by the “craftsman of the heavens”, although I’m leaning towards the first. Unluckily, I did not realize earlier what I have learned now, that mathematics helps turn the soul towards the study of being. The mathematical education I had during my childhood did not urge me to deal with mathematics the way Socrates recommend in Republic VII, but rather in the way suitable for craftsmen and traders. Being in my mid-twenties, a bit behind the philosopher king education-schedule, I do think there is still hope for me, not for the sake of ruling, but for the possibility of grasping the truth behind the world of coming to be and coming to end. I must admit that Plato has convinced me to take a deeper look behind the things in this world and try to grasp the numbers themselves, the forms and the truth with mathematics as a tool and the Good itself as telos.

Literature:

S. Marc Cohen, Patricia Curd, C.D.C. Reeve (2011) Readings in Ancient Greek Philosophy: From Thales to Aristotle. 4th ed. Hackett Publishing Company.

M. F. Burnyeat (2000) Plato on why mathematics is good for the soul. Article available from: http://www.britac.ac.uk/pubs/proc/files/103p001.pdf

Science & Education. April 2008, Volume 17, Issue 4, pp 449–456. I. Caleon & S. Ramanathan: From Music to Physics: The Undervalued Legacy of Pythagoras. Available from:
http://download.springer.com/static/pdf/527/art%253A10.1007%252Fs11191-007-9090-x.pdf?originUrl=http%3A%2F%2Flink.springer.com%2Farticle%2F10.1007%2Fs11191-007-9090-x&token2=exp=1480951161~acl=%2Fstatic%2Fpdf%2F527%2Fart%25253A10.1007%25252Fs11191-007-9090-x.pdf%3ForiginUrl%3Dhttp%253A%252F%252Flink.springer.com%252Farticle%252F10.1007%252Fs11191-007-9090-x*~hmac=4a5b27c65298fd187be9fe636d6f7effba7adf58aff6021fe2ee9acd7de1c279