Elements of Set Theory: Inductive Sets
In mathematics, there are two ways of introducing new objects for study,
- axiomatic approach (e.g. the one we have used for sets)
The concept of set is one of our primitive notions, and we have adopted a list of axioms dealing with the primitive notion. - constructive approach (e.g. )
In this case, we will define the natural numbers in terms of other available objects (sets, of course).
In this section, we would like to introduce the natural numbers for further study. In this case, we will define the natural numbers in terms of other available objects (from sets). And with this, we will prove the necessary properties of numbers from known properties of sets.
Constructing the natural numbers in terms of sets is part of the process of "embedding mathematics in set theory".
Inductive Sets
First we need to define natural numbers as suitable sets. These numbers at first glance will not appear as sets. They are abstract concepts, which are slippery things to handle. Nevertheless, we can construct specific sets that will serve perfectly well as numbers.
In 1908, Zermelo proposed to use
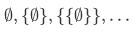
as the natural numbers.
von Neumann proposed an alternative, which has become a standard as it has several advantages. The idea behind von Neumann's construction is to make each natural number be the set of all smaller natural numbers. Considering the first four natural numbers, it follows:
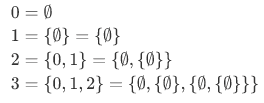
Neumann associated a number to a particular set.(Note that the number associated on the left is the number of members of a set on the right side.) This construction of the numbers as sets involves some extraneous properties that we did not originally expect. For example,
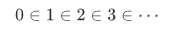
and
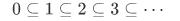
Note that these properties are merely side effects of the definition (by Neumann). They prove to be useful in later parts.
Actually, we haven't introduced yet the definition of what it means to be a natural number. We have not defined the set of all natural numbers yet.
First, we define some preliminary concepts.
Definition For any set a, its successor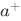 
is defined by
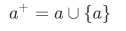
A set A is said to be inductive iff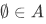 
and it is "closed under successor" i.e.,
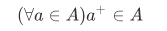
In terms of the successor operation, the first few natural numbers can be characterized as,
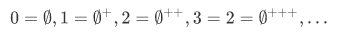
Note that these are all distinct, such that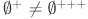 
. And even though we haven't introduced the formal definition of "infinite", we can see informally that any inductive set will be infinite.
Infinity Axiom There exists an inductive set:
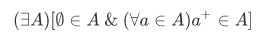
Armed with this axiom we can now define the concept of natural numbers.
Definition A natural number is a set that belongs to every inductive set.
A little recap:
Neumann introduce the standard definition of a natural numbers. We then move to some preliminary concepts such as successor, which was useful in the infinity axiom, and inductive sets to help introduce the formal definition of natural number.
We next prove that the collection of all natural numbers constitutes a set.
Theorem 4A There is a set whose members are exactly the natural numbers
The set of all natural numbers is denoted by a lowercase Greek omega:
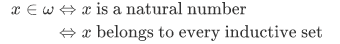
In terms of classes we have,
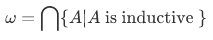
but the class of all inductive sets is not a set.
Theorem 4B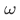 
is inductive and is a subset of every other inductive set.
Hence \omega is inductive. And clearly 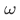is included in every other inductive set. Since 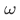is inductive, we know that 0 
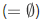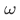is in . It then follows that 1 
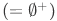is in 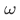, as are 2 
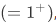and 3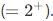 
Thus 0,1,2,3 are natural numbers. This fact can be restated as follows
Induction Principle for 
: Any inductive subset of coincides with .
The next theorem gives a very simple example of the induction method.
Theorem 4C Every natural number except 0 is the successor of some natural number.
Disclaimer: this is a summary of section 4.1 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshots from generated latex form using typora
Thank you for reading ...
