What does the mean value theorem tell you about the speed you travelled!
We only measure the average speed that we travelled when we calculate the velocity of driving a car from point A to point B. But what can the average velocity tell you about your true velocity? This is where the Mean Value Theorem comes into play!
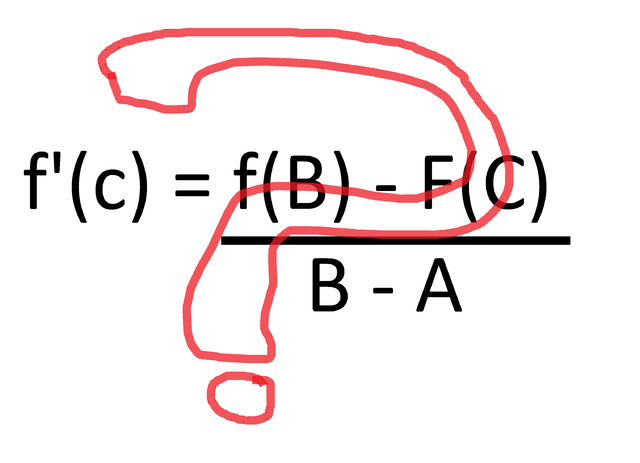
Check out why it is you average velocity here on my calculus paradox post over here
The Mean Value Theorem (MVT) states the following, if the curve is :
Continuous on the interval from A to B ( in mathematical terms [A,B] )
Differentiable on the interval on the interval A to B excluding A and B ( in mathematical terms (A,B) )
Then there exists a point C on the interval AB such that the slope of point C is equal to the average slope value of the curve AB. here is a graphical illustration of this theorem:
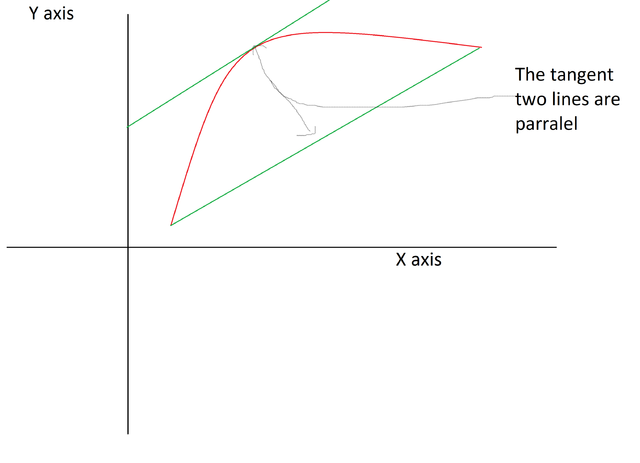
Intuitive explanation:
Let's think about a curve like this:
You can cut a line through any two points like this:
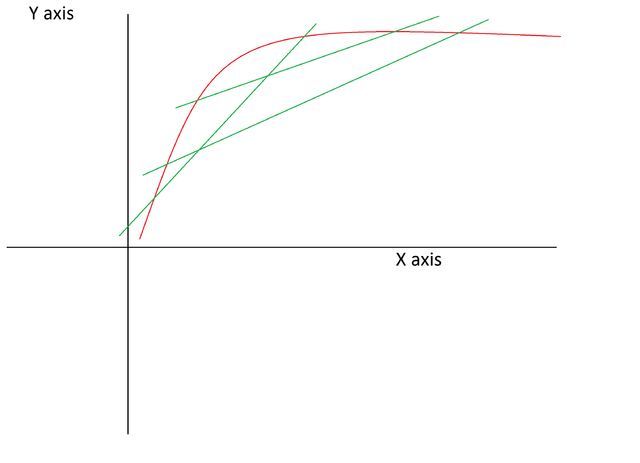
Let’s look at this line AB:
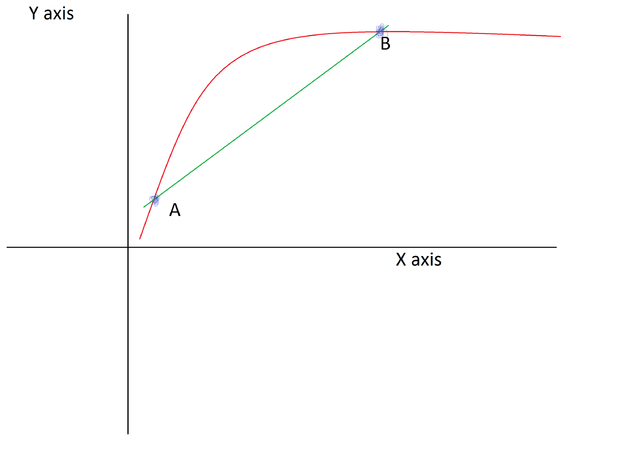
what if we took that curve and just rotate it so that the line AB is horizontal with the x - axis like this:
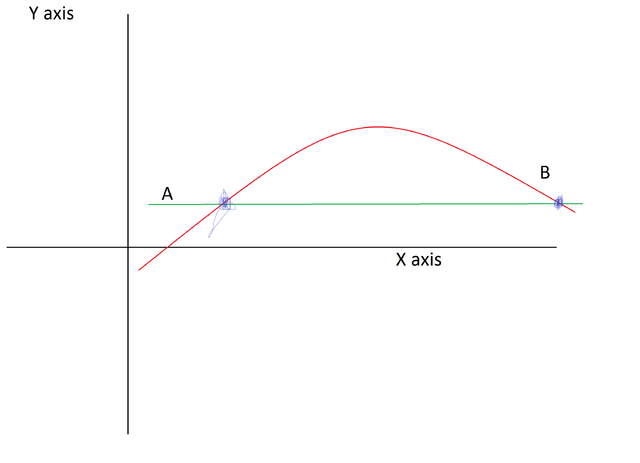
This would mean that the slope of the line AB is equal to 0. Notice how the points A and B lie on the same height on the Y axis. From this Rolle’s theorem would apply (If you want to see its proof click here) and it states somewhere on the interval of A and B there is a point C such that the slope of the point C is equal to 0. This would mean that the line AB has the same slope as the point C on the interval of AB. This would mean that the mean value theorem is true!
This happens because the slope of a curve changes at a smooth continuous rate, this would mean it must bend or curve reach from point A to reach Point B. Somewhere on this interval the function must have the same slope like the line AB.
You can test this with a circle or any curve, a ruler and a pencil. Place the pencil to cut any two points of the curve like this:
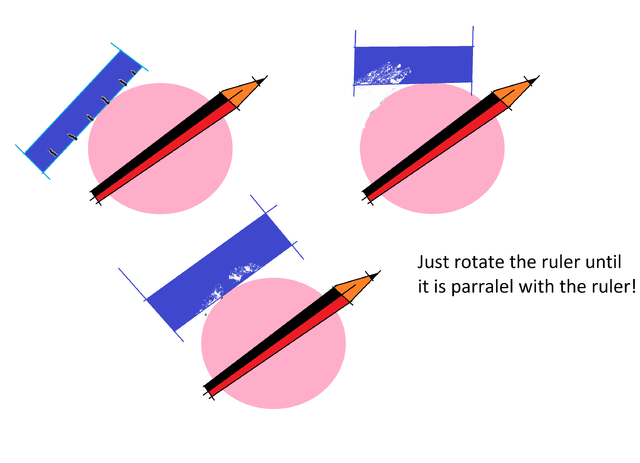
***Sorry for the mistakes that i made in my picture! It was meant to say until it is parallel with the pencil ***
Then you can slide the ruler along the curve of the circle until it is parallel with the pencil.
Now that we have seen this theorem apply in the real world, lets see the Mathematical proof.
Mathematical proof!
We need Rolle’s theorem in this proof, once again you can see the theorem here. Here is a summary of Rolle’s theorem. If a function has the following properties:
It is continuous on the interval AB
It is differentiable on
The output of A = output of B
Then there is a point C on the interval A and B (mathematically denoted C E (A,B) such that the slope of point C is equal to 0.
Now let us start the proof with some assumptions:
Lets us assume there exists a function f such that it:
Continuous on interval AB ( [A,B] )
Differentiable on interval AB excluding A and B ( (A,B) )
Now let’s draw a green line from point A to point B and we will call it G(x):
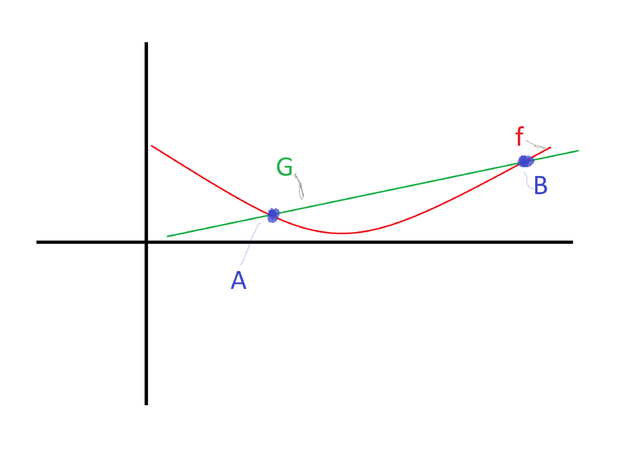
G's slope is equal to the change in y divided to the change in x thus it is as the following:
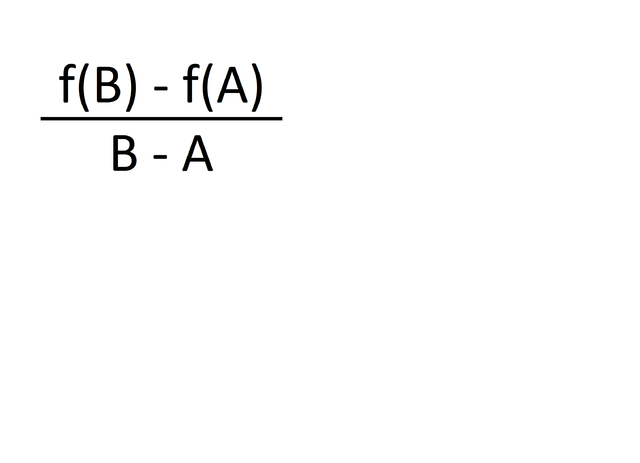
This slope is constant due to derivative properties of a straight line. The equation of a line is given in the following form:
y - y1 = m( x - x1)
Where:
y1 is a y coordinate on the function G
x1 is an x coordinate on the function G
and m is the slope of the function G
If the add a y1 on both sides of the equation we get this:
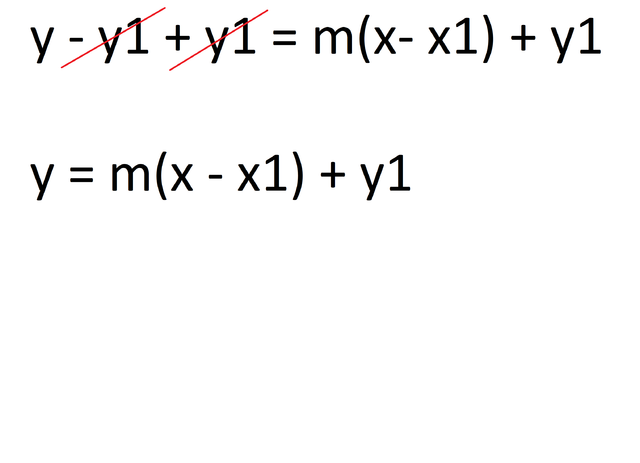
please note that G(x) = y because G(x) is just another way to write y
We know the point A is a point that lies on the function G and its coordinate is
y = f(A) and x = A
Thus, y1 and x1 can be replaced with f(A) and A respectively.
And we know:

Thus, the equation of function G is written as the following:
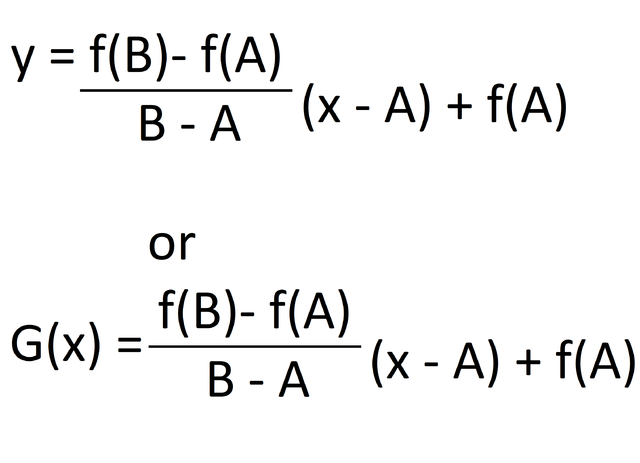
Now we can create a new function h. Function h is defined as function f - function G.
So the equation of function f is as follows:
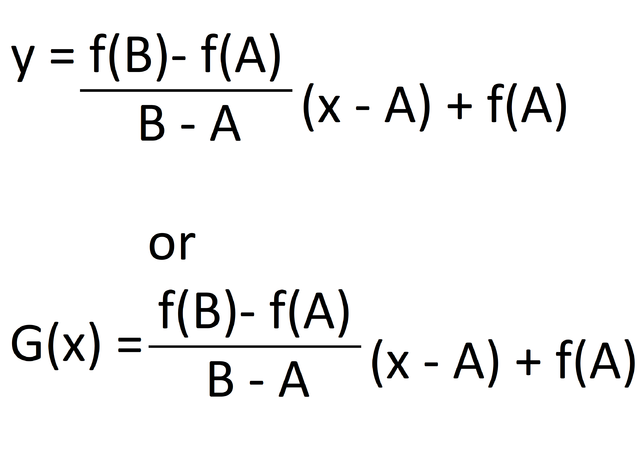
Now h is continuous because f and g is both continuous
h(x) also differentiable because f and g is differentiable.
h(x) = 0 at the points A and B
Because at A and B f = g
thus f - g = 0 at A and B
Now we wish to apply Rolle’s theorem since h(x) is continuous and differentiable on the interval A and B and h(A) = h(B). Rolle’s states exist a point C on the interval A and B such that the slope of point C = 0. The slope of h(x) looks like the following equation:
We know there is a point c such that f’(C) = 0 but:

Thus, the statement is proven!
MVT tells us that some point on your journey you did at least travel at the velocity as your calculated average velocity! This is a nice theorem and has a creative way to prove this theorem!
As always thanks for reading!
This is really fun to make but please Resteem, I make most of my images for my proof posts, today I made every image on this post, now i know It does not look tooo great, but it takes time and care ( I did make a mistake on one photo, hey I am a human being!) Thank you for the support and great feedback! Enjoy your day and keep thinking!
what do you think? leave a comment down below. Do not forget to upvote, Resteem and follow my blogspot!
check out more posts Here

Always fun to read this paradox, you have to love calculus to appreciate the beauty of it! :D
I agree with you 100% Thank for supporting and commenting on my post yet again, I really appreciate it!
:)
Thanks. I'd like to include this in the next mathematics magazine (N.4 can be found here). Hope that's OK with you.
!-=o0o=-!
To follow curated math content follow @math-trail.
If you wish @math-trail to follow you then read this article.
Click here for Mathematics forum on chainBB
Well written stormblaze