Mathematical Explanation - The Wave Equation
Hello friends, continuing with my series of publications related to the science of mathematics, today in this publication I want to refer to the equation of the wave, which is considered as the mathematical expression that allows us to know the state of vibration of any point from the middle at any time. To deduce this equation is required to know the mathematical parameters that define it for it here I will explain your deficion and also talk about the equations that define the wave, I invite you to observe this interesting post!
Welcome to the wonderful world of mathematics ....
Wave equation
The wave equation is an important differential equation in linear partial derivatives of second order that describes the propagation of a variety of waves, such as sound waves, light waves and waves in water. It is important in several fields such as acoustics, electromagnetism, quantum mechanics and fluid dynamics. Historically, the problem of a vibrating string like those found in musical instruments was studied by Jean le Rond d'Alembert (1746) for the first time, Leonhard Euler (1748), Daniel Bernoulli (1753) and Joseph-Louis Lagrange (1759). ). Solutions were found in various forms that caused discussions for more than twenty-five years. The disputes were still resolved in the 19th century.
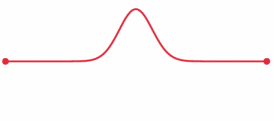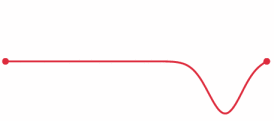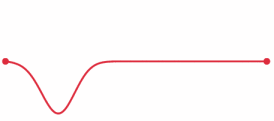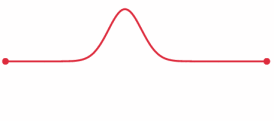
A pulse that travels through a string with its fixed ends is modeled by the wave equation.
Introduction
The wave equation is the prototype example of a hyperbolic equation in partial derivatives. In its most elementary form, the wave equation refers to a function u (x, t) that satisfies:
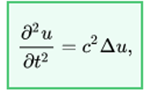
Where  is the Laplacian and where {\ displaystyle c} c is a constant equivalent to the speed of propagation of the wave. For a sound wave in the air at 20 ° C, this constant is about 343 m / s (see speed of sound). For a vibrating string, the speed can vary greatly depending on the linear density of the string and its tension. For a spiral spring (a Slinky) it can be as slow as one meter per second.
is the Laplacian and where {\ displaystyle c} c is a constant equivalent to the speed of propagation of the wave. For a sound wave in the air at 20 ° C, this constant is about 343 m / s (see speed of sound). For a vibrating string, the speed can vary greatly depending on the linear density of the string and its tension. For a spiral spring (a Slinky) it can be as slow as one meter per second.
A more realistic model of the differential equation for waves allows the speed of propagation of the wave to vary with the frequency of the wave, this phenomenon is known as dispersion. In this case, c must be replaced by the phase velocity:
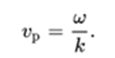
Another common correction in realistic systems is that the speed can also depend on the amplitude of the wave, which leads to a non-linear wave equation:
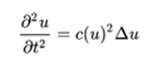
It must also be considered that a wave can be transmitted on a mobile carrier (for example, the propagation of sound in the flow of a gas). In this case the scalar u will contain a Mach number (which is positive for the wave that moves along the flow and negative for the reflected wave).
The elastic wave equation in three dimensions describes the wave propagation in an isotropic homogeneous elastic medium. Most solid materials are elastic, so that equation describes phenomena such as seismic waves on Earth and ultrasound waves used to determine defects in materials. Although it is linear, this equation has a more complex shape than the equations given above, because it must take longitudinal and transverse movements into account:
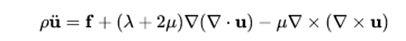
Where :
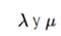 are the supposed parameters of Lamé that describe the elastic properties of the medium.
are the supposed parameters of Lamé that describe the elastic properties of the medium.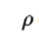 is the density,
is the density,- f is the input function (motive force),
and u is the displacement.
Note that in this equation, force and displacement are vector quantities. This equation is sometimes known as the vector wave equation.
There are variations of the wave equation that can also be found in quantum mechanics and general relativity.
Problems with borders
In the space of a single dimension
A flexible chain stretched between two points x = 0 and x = L satisfies the wave equation, for t> 0 and 0 <x <L. At border points, u can satisfy a variety of boundary conditions. A general form that is appropriate for applications is
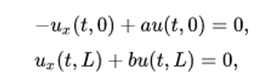
where a and b are not negative. The case where u is required to disappear at a final point is at the limit of this condition when the respective a or b approaches infinity. The method of separation of variables consists of finding solutions for this problem in the spatial form
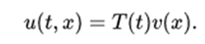
One consequence is that
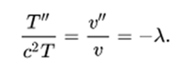
The eigenvalue λ must be determined in such a way that there is a non-trivial solution to the border value problem
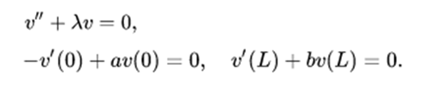
This is a special case of the general problem of the Sturm-Liouville theory. If a and b are positive, the eigenvalues are all positive and the solutions will be the trigonometric functions. A solution that satisfies the initial condition integrable to the square for u and ut can be obtained from the expansion of these functions in the appropriate trigonometric series.
The theory
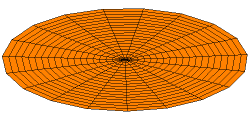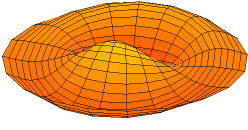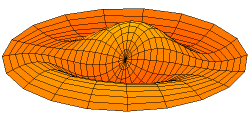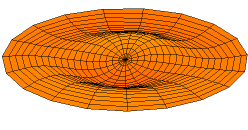
A solution of the two-dimensional wave equation with a boundary condition of zero displacement along the entire outer edge.
The theory of the initial unidimensional boundary value can be extended to an arbitrary number of spatial dimensions. Consider a domain D in a space x of m dimensions, with boundary B. Then the wave equation will be satisfied if x is in D and t> 0. At border B, the solution u must satisfy
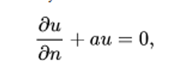
where n is the unit normal to B that points outward and a is a non-negative function defined on B. The case where u disappears at B is a limiting case when a approaches infinity. The initial conditions are
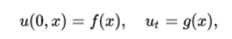
where f and g are defined in D. This problem can be solved by expanding f and g in the Laplacian functions in D, which meet the boundary conditions. Thus, the proper function v satisfies
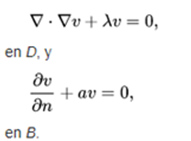
In the case of a two-dimensional space, the proper functions can be interpreted as the modes of vibration of a membrane extended over the boundary B. If B is a circle, then these auto-functions have an angular component that is a trigonometric function of the polar angle θ, multiplied by a Bessel function (of integer order) of the radial component. Further details are found in the Helmholtz equation.
If the boundary is a sphere in a three-dimensional space, the angular components of the proper functions are spherical harmonics, and the radial components are Bessel functions of half-order.
Below are a series of practical exercises, where the equation of the wave is applied:
1.- Heat
A metal rod 100cm long has the ends x = 0 and x = 100, maintained at 0 ° C. Initially half of the bar is at 60 ° C, while the other half is at 40 ° C. Assuming a thermal diffusivity of 0.16 cm2 / sec, and that the surface of the bar is isolated, find the temperature in all parts of the bar at time t.
Heat equation
∂U / ∂t = k (∂ ^ 2 U) / (∂x ^ 2)
Main equation of the problem
U (x, t) = X (x) ∙ T (t)
Terms
U (0, t) = 0
U (x, 0) = {(60 @ 40) (0 <x <50 @ 50 <x <100) }
Deriving the main equation according to the heat equation
X ∙ T'= 0.16X'' ∙ T
Applying separation of variables
(X'') / X = (T') / 0,16T = -λ ^ 2
Note: They must be equal to (-2), since by definition to equal the two terms must be equal to this constant.
Forming the equations and equaling them to zero
- X'' + λ ^ 2 X = 0
- T'+ 0,16λ ^ 2 T = 0
Solving equations 1 and 2
- X'' + λ ^ 2 X = 0
X = e ^ mx by definition, then substituting
(e ^ mx) '' + λ ^ 2 (e ^ mx) = 0
m ^ 2 e ^ mx + λ ^ 2 e ^ mx = 0
e ^ mx (m ^ 2 + λ ^ 2) = 0
m = √ (-λ ^ 2)
Note: since the value of m gives us an imaginary number by definition we will have:
X (x) = C1 cos 〖λx + C2 sinλx〗
- T'+ 0,16λ ^ 2 T = 0
T = e ^ mt by definition, then substituting
(e ^ mt) '+ 〖0,16λ〗 ^ 2 (e ^ mt) = 0
me ^ mt + 〖0.16λ〗 ^ 2 e ^ mt = 0
e ^ mx (m + 〖0.16λ〗 ^ 2) = 0
m = - 〖0,16λ〗 ^ 2
So:
T (t) = e ^ (- 〖0,16λ〗 ^ 2 t)
Evaluating condition X (0) = 0
C1 cos 〖λ (0) + C2 sinλ (0)〗 = 0
C1 = 0
Note: If C1 = 0, then C2 ≠ 0 to not have a trivial solution
C2 sinλx = 0
is replaced by λ = nπ / L, by definition
Substituting λ = nπ / L in the equations
X (x) = C2 sin 〖nπx / L〗
T (t) = e ^ (- 〖0.16 (nπ / L)〗 ^ 2 t)
Note: Since the sine is an odd function corresponds a bn
b_n = 1 / L ∫ _ (- L) ^ L▒ 〖f (x) ∙〗 sin 〖nπx / L〗 dx
simplifying to facilitate its resolution, we have:
b_n = 2 / L ∫0 ^ L▒ 〖f (x) ∙〗 sin 〖nπx / L〗 dx
U (x, t) = Σ (n = 1) ^ ∞▒ 〖b_n ∙〗 sin 〖nπx / L〗 ∙ e ^ (- 〖0.16 (nπ / L)〗 ^ 2 t)
2.- Border value
Consider a thin rod of length L with a longitudinal distribution of temperature f (x), and whose ends are maintained at a temperature of 0 ° C, at all times, then the temperature U (x, t) is given by the boundary solution.
Heat equation
∂U / ∂t = k (∂ ^ 2 U) / (∂x ^ 2)
Main equation of the problem
U (x, t) = X (x) ∙ T (t)
Terms
U (0, t) = 0
U (x, 0) = f (x) = 1
Deriving the main equation according to the heat equation
X ∙ T'= KX'' ∙ T
Applying separation of variables
(X'') / X = (T') / 0,16T = -λ ^ 2
Note: They must be equal to (-2), since by definition to equal the two terms must be equal to this constant.
Forming the equations and equaling them to zero
- X'' + λ ^ 2 X = 0
- T'+ 0,16λ ^ 2 T = 0
Note: Applying the same resolution as the previous exercise we have:
X (x) = C1 cos 〖λx + C2 sinλx〗
T (t) = e ^ (- kλ ^ 2 t)
Evaluating the condition U (0, t) = 0, where X (0) = 0
C1 cos 〖λ (0) + C2 sinλ (0)〗 = 0
C1 = 0
Note: If C1 = 0, then C2 ≠ 0 to not have a trivial solution
C2 sinλx = 0
is replaced λ = nπ / L, by definition in the equations
X (x) = C2 sin 〖nπx / L〗
T (t) = e ^ (- 〖k (nπ / L)〗 ^ 2 t)
Note: Since the sine is an odd function corresponds a bn
b_n = 1 / L ∫ _ (- L) ^ L▒ 〖f (x) ∙〗 sin (nπ) dx
simplifying to facilitate its resolution, we have:
b_n = 2 / L ∫0 ^ L▒ 〖sin 〖nπx / L〗 dx〗
U (x, t) = Σ (n = 1) ^ ∞▒ 〖(2 / L ∫_0 ^ L▒ 〖sin 〖nπx / L〗 dx〗) ∙〗 sin 〖nπx / L〗 ∙ e ^ (- 〖k (nπ / L)〗 ^ 2 t)
3.- Rope
Solve the wave equation, subject to the conditions cited in the problem:
Y (0, t) = 0; Y (x, 0) = 0; Y_t (x, 0) = 1
Wave equation
(∂ ^ 2 Y) / (∂t ^ 2) = a ^ 2 (∂ ^ 2 Y) / (∂x ^ 2)
Main equation of the problem
U (x, t) = X (x) ∙ T (t)
Terms
Y (0, t) = 0
Y (x, 0) = 0
Y_t (x, 0) = 1
Deriving the problem equation
- X'' + λ ^ 2 X = 0
- T'' + a ^ 2 λ ^ 2 T = 0
Note: Because the equations are of the 2nd order, and because they have imaginary roots, then the solutions X (x) and T (t), will have the following form:
X (x) = C1 cos 〖λx + C2 sinλx〗
T (t) = C3 cos 〖aλt + C4 sinaλt〗
Evaluating the condition Y (0, t) = 0, where X (0) = 0
C1 cos 〖λ (0) + C2 sinλ (0)〗 = 0
C1 = 0
Note: If C1 = 0, then C2 ≠ 0 to not have a trivial solution
C2 sinλx = 0
is replaced λ = nπ / L, by definition in the equations
X (x) = C2 sin 〖nπx / L〗
Note: Since the sine is an odd function it will have coefficients bn in the series
T (t) = C3 cos 〖anπt / L + C4 sin 〖anπt / L〗〗
Y (x, t) = C2 sin 〖nπx / L〗 (C3 cos 〖anπt / L + C4 sin 〖anπt / L〗〗)
the condition Y (x, 0) = 0 is evaluated
Y (x, 0) = C2 sin 〖nπx / L〗 (C3 cos 〖anπ / L or + C4 sin 〖anπ / L or〗〗)
b_n1 = sin 〖nπx / L〗 = 0⟹b_n1 = 0
so:
Y (x, t) = (b_n2 sin 〖anπt / L〗) 〖∙ sin〗 〖nπx / L〗
deriving Y (x, t):
Y_t' (x, t) = (anπ / L b_n2 cos 〖anπt / L〗) 〖∙ sin〗 〖nπx / L〗
the condition Y_t (x, 0) = 1 is evaluated
(anπt / L b_n2 sin 〖anπt / L〗) 〖∙ sin〗 〖nπx / L〗 = 1
F (x) = anπ / L b_n2 〖∙ sin〗 〖nπx / L〗 = 1
bn2 = bn because I consider it to be a function of the sine
b_n=2/L ∫0^L▒〖sin〖nπx/L〗 dx〗=2a/L (1-cosnπ )
Y(x,t)=∑(n=1)^∞▒〖(2a/L (1-cosnπ ))∙〗 sin〖anπt/L〗∙sin〖nπx/L〗
Bibliography
- M. F. Atiyah, R. Bott, L. Garding, "Lacunas for hyperbolic differential operators with constant coefficients I", Acta Math., 124 (1970), 109-189.
- M.F. Atiyah, R. Bott, and L. Garding, "Lacunas for hyperbolic differential operators with constant coefficients II", Acta Math., 131 (1973), 145-206.
- R. Courant, D. Hilbert, Methods of Mathematical Physics, vol II. Interscience (Wiley) New York, 1962.
- "Linear Wave Equations", EqWorld: The World of Mathematical Equations.
- "Nonlinear Wave Equations", EqWorld: The World of Mathematical Equations.
- William C. Lane, "MISN-0-201 The Wave Equation and Its Solutions", Project PHYSNET.
- Relativistic wave equations with fractional derivatives and pseudodifferential operators, by Petr Zavada, Journal of Applied Mathematics, vol. 2, no 4, pp. 163-197, 2002. doi: 10.1155 / S1110757X02110102 (available online or as the arXiv prepress)
References
- Boyce / Di Prima: "Differential equations and problems with values at the border" p. 585
Hello,
We have found similar content: https://es.wikipedia.org/wiki/Ecuaci%C3%B3n_de_onda
Not indicating that the content you post including translations, spun, or re-written articles are not your original work could be seen as plagiarism.
These are some tips on how to share content and add value:
Repeated plagiarized posts are considered spam. Spam is discouraged by the community, and may result in action from the cheetah bot.
If you are actually the original author, please do reply to let us know!
Thank You.
More Info: Abuse Guide - 2017.
This post has received a 2.90% upvote from @lovejuice thanks to @freyman. They love you, so does Aggroed. Please be sure to vote for Witnesses at https://steemit.com/~witnesses.