TRI-TRIADIC SCALES WITH 7 TONES (Just Intonation and Equal Temperament)

With the exception of pentatonics, seven tone scales are the most widespread type in world music. Whether this near universality is due to psychological preferences or to innate structural superiority is as yet undecided, but heptatonic scales are attested from the the second millenium BC in the near East. Since the time of Rameau, it has been recognized that scales of the major and minor type may be partitioned into three triads on roots separated by a perfect fifth. AJ Ellis extended this approach and derived the tones of European modal music from the circular permutations of scales with mixed triads. In 1982, David Lewin generalized the concept to include all scales generable from three identical triads on three equally spaced roots under the name of Riemann Systems, which consist of a tonic (T), a dominant (D) and a mediant (M). In independent investigations, these ideas were applied to scales with more than seven tones in non-twelve tone equal temperment by John Chalmers, and to seven tone scales constructed from non-major or minor triads by Chalmers, and by Ervin Wilson, who suggested the term tritriadic as a replacement for Ellis's somewhat ambiguous "trichordal."

Tritriadic scales may be described by a dominant (D) and a mediant (M) above an arbitrary tonic (T), defined as 0 cents in equal temperament or 1/1 in just intonation. Tritriadic matrices are constructed from T, D, and M in analogy with the fundamental harmonization of the major and minor scales.

The above scalar matrices are modulo 1200 or 12/1. In the case of the major scale the tonic chord is 0 400 700 or 4:5:6 (1/1 5/4 3/2).

If the magnitudes of D and M are allowed to vary over the range from 0 to 1200 cents, the tonal space DxM will be divided into 32 regions, which correspond to the 32 possible types of tritriadic scales with identical scales. The scales consist of 16 classes related by inversion. As may be seen in the illustration below (Figure 1), the scales consist of 16 classes related by inversion. For examples, type III-2, which includes major and minor modes, is inversionally paired with type II-3, which contains the same intervals in reverse order, i.e., the major scale (T, D, M) is paired with its inverted type (T, -D, -M). This scale has been variously known as the Greek Dorian, Blainville's "Third Mode" or Von Oettingen's "Phonic System."

Figure 1

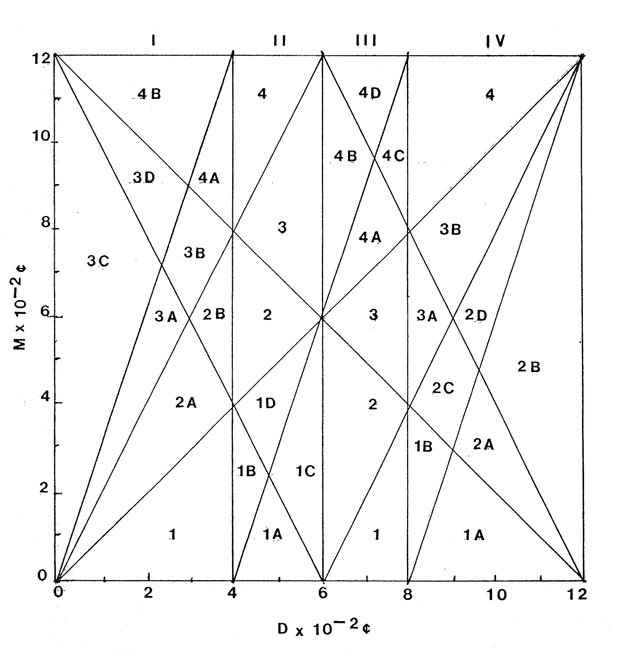
The restrictions on the sizes of D and M which define the various scalar classes are the following:

D() 0, 400, 600, 800, or 1200 cents.
M() 0, +D, +2D, +3D modulo 1200 cents.

These conditions are sufficient to partition D into 4 domains:

I 0<D<400 cents
II 400<D<600 cents
III 600<D<800 cents
IV 800<D<1200 cents

which define the 4 major types. Classes and subclasses are determined by the size of M in relation to the positions of D, 2D, and -D. Although each of these scales comprises three acoustically identical triads, these triads do not necessarily consist of alternate scale degrees or even of melodically equivalent intervals. In fact, only type III-2 scales have tertian chords, and only six of the 32 types have triads of melodically identical form. These consistent types and their triads expressed as ascending scalar intervals (0-M, M-D) are given below:

The inversional pairing can be seen here, too. Type III-2 is harmonized with triads built of thirds, while its inverse II-3 employs sixths.

All the other types of triads whose component intervals, though acoustically identical, span different numbers of scale degrees. The result suggested that an examination of the propriety or coherence might be informative. It was discovered by solving the requisite inequalities in terms of D and M that only 16 types contained proper or strictly proper tunings. In six cases, the only proper solutions were points corresponding to modes of the scale, 0 1 2 3 4 5 6 in 8-tone equal temperament. Four other types had proper solutions which consisted of lines. The six types with consistent triads alone had strictly proper solutions, which appear as the interiors of polygonal subregions within the regions of Figure 1 (see above). Only these types have strictly proper solutions in just intonation. The final mode of the seven tone out of eight scale occurs as an extremal point of one of these regions. Of the total DxM space, only about 3% is covered by proper tunings, indicating that such scales are rare.

The set of 32 types of tritriadics was mapped into the equal temperaments which have from seven to twenty-four tones per octave. Fourteen-tone equal temperament was the first to contain all 32 types, and types 1-3C and IV-2B were the most frequent. Such scales are a feature of tonal music - the harmonic and melodic minor modes.

As stated before, the six consistent types are the only ones with proper solutions in just intonation. While improper scales are used in many musical cultures, including "western" music (Hungarian minor), they require different treatment from the proper scales which are more familiar to western musicians.