Aplicaciones de las superficies cuádricas // Caso paraboloide hiperbólico (silla de montar caballos)
En esta oportunidad voy a dar inicio a una nueva serie temática dedicada a una parte de la geometría que tiene íntima relación con el cálculo infinitesimal, tal es el caso de las superficies cuádricas. Existe una ecuación general de las superficies cuádricas, y de la cual se derivan las siguientes figuras geométricas:
- Elipsoide.
- Hiperboloide elíptico de una hoja.
- Hiperboloide elíptico de dos hojas.
- Paraboloide elíptico.
- Paraboloide hiperbólico (objeto de estudio en esta publicación).
- Cono elíptico.
A continuación se muestra la ecuación general de las superficies cuádricas:
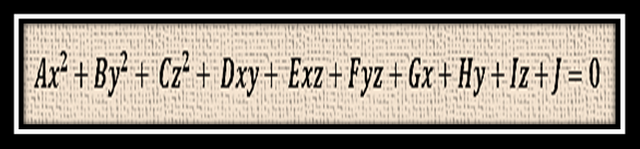
Para todos aquellos que alguna vez en un curso de precálculo haya visto la gráfica de la ecuación de segundo grado de dos variables puede tratar de analizar, y se dará cuenta que la ecuación general de la superficies cuádricas presentada anteriormente deriva de la anterior, solo que la presentada arriba tiene la referencia de tener tres variables (xyz).
Esa representación de las superficies cuádricas se pueden expresar en forma de función de dos variables, por ejemplo en el caso que estamos tratando del paraboloide hiperbólico, podemos realizar las siguientes deducciones:
Se asume que D, E, F, G, H, I y J son iguales a cero, por lo que se cancelan de la ecuación general de las superficies cuádricas.
Asumiendo que los coeficientes D, E, F, G, H, I y J son iguales a cero se deriva la siguiente ecuación:
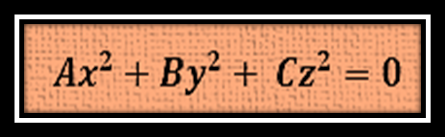
Autor de la imagen: @carlos84 Partiendo de esta ecuación, para que sea paraboloide debe poseer parábolas, por lo que resulta necesario que la variable z no esta elevada al cuadrado, si lo analizamos desde el punto de vista de una función de dos variables es necesario que la variable que no esté al cuadrado sea z, ya que cuando z queda despejada es función de (x,y).
Una de las dos variables (x o y) debe ser negativa, ya que de esta forma se generan en los diferentes planos: una parábola y dos hipérbolas, de allí es que resulta la superficie cuádrica llamada paraboloide hiperbólico o silla de montar caballos.
Tomando en cuenta las consideraciones nombradas nos queda que la ecuación del paraboloide hiperbólico queda de la siguiente manera:
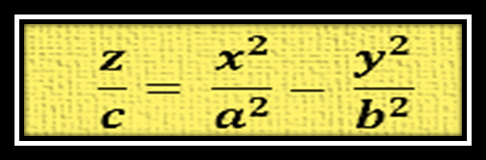
En este caso la variable (x o y) que quede positiva, será el eje donde abrirá la parábola, para este caso abrirá en el eje x. La variable que quede negativa, lo cual para este caso es la variable y, será el eje donde se graficaron las dos hipérbolas.
Las gráficas en sus respectivos planos quedarían de la siguiente manera:
- Plano xy: asumiendo z=0, serían dos rectas que se interceptan en el origen.
- Plano xz: Una parábola cuando y = k
- Plano yz: Una parábola cuando x = k
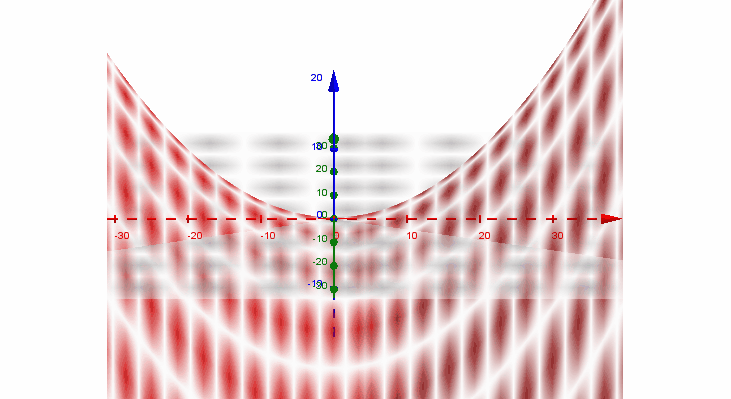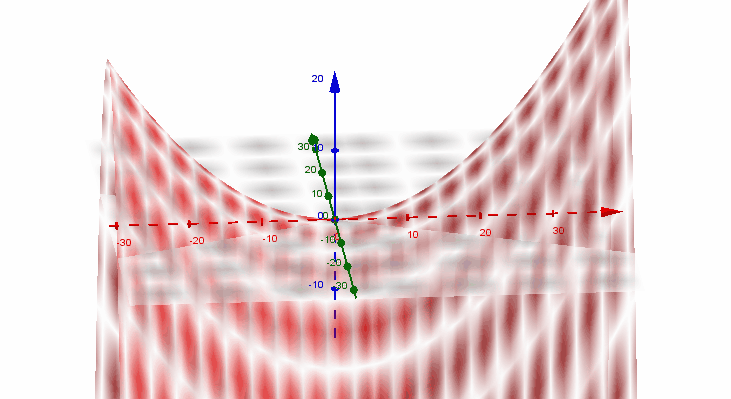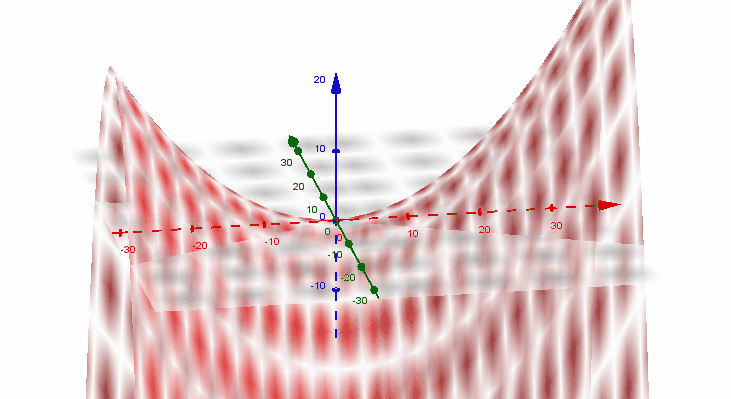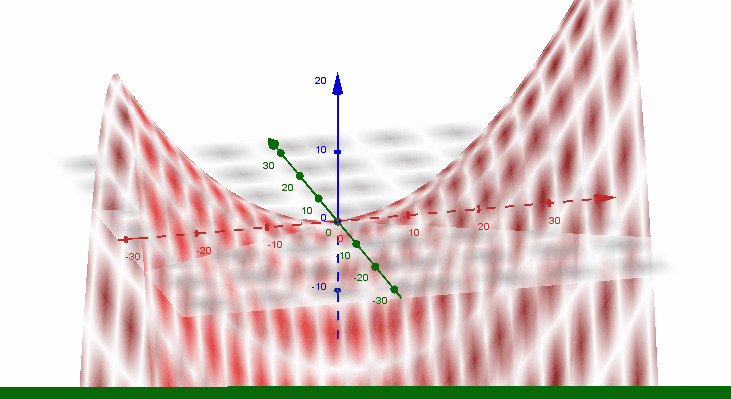
Gráfica del paraboloide hiperbólico en el sistema tridimensional (x,y,z)
Para mostrar la gráfica del paraboloide hiperbólico se tomará en cuenta la ecuación del paraboloide hiperbólico mostrado en este artículo, Le daremos valores arbitrarios (a,b y c) donde a y b deben ser distintos de cero y c debe ser estrictamente mayor a cero.
Para graficar el paraboloide hiperbólico utilizar el software geogebra 5.0, considerando que a = 9 y b = 4 y c = 2, se puede obtener la gráfica de la ecuación del siguiente paraboloide hiperbólico:
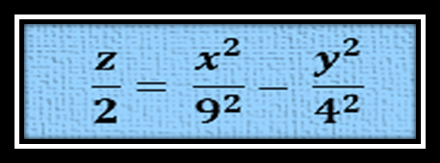
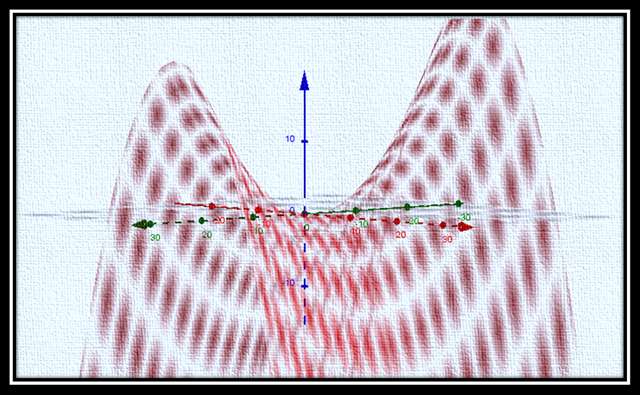
Para tener una descripción de diferentes ángulos del paraboloide hiperbólico o silla de montar caballos, muestro la siguiente imagen gif:
Implicaciones del paraboloide hiperbólico en la vida cotidiana
Las implicaciones que tiene el paraboloide hiperbólico en la vida cotidiana radica en que muchas cosas de la actualidad se asemejan a la forma del paraboloide hiperbólico, la tecnología en materia de construcción y diseño de obras ha evolucionado en construir complejos, estadio de futbol y en general obras arquitectónicas que copian en su forma y estructura geométrica al paraboloide hiperbólico.

Pudiéramos pensar que la forma geométrica del paraboloide hiperbólico pueda resultar llamativa en la realización de algún producto alimenticio procesado, y si así lo pensamos, pues estamos en lo cierto la industria Pringles revolucionó el mercado de las papas fritas presentando un tipo de alimento procesado, en donde la forma ondulada de las papas fritas se asemeja a la del paraboloide hiperbólico.

Inclusive otros nombres encontrados para el paraboloide hiperbólico en libros de cálculo y geometría es silla de montar caballos, esto es debido a la forma geométrica de la silla de montar caballos que resulta muy similar a la forma del paraboloide hiperbólico.

Conclusiones y consideraciones finales
Este tipo de superficies cuádricas tienen una fuerte implicación en el uso y aplicación que se le da en la actualidad, y es que ha sido usada su forma geométrica en la construcción de obras de arte, edificios, estadios de fútbol, entre otras más.
Existe una razón muy clara para construir obras civiles y de carácter arquitectónico en base al paraboloide hiperbólico, y es que esta forma geométrica ofrece resistencia a las fallas o cedencia a la fractura (tensión o compresión), es por ello que la forma de las papas pringles son como la forma del paraboloide hiperbólico, ya que de esta forma se puede acomodar dentro del cilindro sin que estas se quiebren
Este tipo.Por último puedo concluyo con el siguiente análisis:
"La naturaleza y la matemática se unen para crear y fortalecer vínculos infinitos de sabiduría. Y es que en la naturaleza de seguro encontraremos muchos elementos que se adoptaran a la forma del paraboloide hiperbólico, siempre buscando tener la forma geométrica que mejor se adapte a las esfuerzos de tensión y compresión a los que muchas veces somos sometidos en condiciones normales, razón por la cual el avance tecnológico en las construcciones, almacenamientos de productos, y otras tecnologías de seguro evolucionarán buscando la forma geométrica del paraboloide hiperbólico".
Hasta una próxima entrega de este servidor. Saludos
Bibliografía consultada
- Libro de Cálculo con Geometría Analítica. Autor: Larson y Hostetler. Volumen II.
Lecturas recomendadas
Herramientas utilizadas
Software matemático: geogebra 5.0
Editor de imágenes de Microsoft Word 2010 y Microsoft PowerPoint 2010.
Editor de ecuaciones matemáticas de Microsoft Word 2010.

¡Felicitaciones!
Estás participando para optar a la mención especial que se efectuará el domingo 25 de agosto del 2019 a las 8:00 pm (hora de Venezuela), gracias a la cual el autor del artículo seleccionado recibirá la cantidad de 1 STEEM transferida a su cuenta.
¡También has recibido 1 ENTROKEN! El token del PROYECTO ENTROPÍA impulsado por la plataforma Steem-Engine.
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Contáctanos en Discord.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Muchas gracias, Carlos. Has cambiado mi visión de las Pringles.
Agradecido de que te hayas tomado el tiempo de leer este post. Saludos
Gracias por el apoyo al equipo de cervantes y en especial @ramonycajal. Saludos
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Please consider setting @steemstem as a beneficiary to your post to get a stronger support.
Please consider using the steemstem.io app to get a stronger support.
Gracias por el poyo al equipo de steemstem. Saludos