Wszystko i nic #2
Słówko wstępu...znów

Moja regularność rozłożyła się na pierwszym kolokwium i z dwóch tygodni zrobiły się dwa miesiące...ale co się odwlecze to nie uciecze więc przez święta postaram się nadrobić zaległości. Dzisiaj bardziej matematycznie (Obiecałem wpis o paradoksach, ale trochę zmienię plany i tym zajmę się w trzecim lub czwartym wpisie).
Dlaczego każda liczba podniesiona do potęgi 0 da jeden?
Każdy kto miał jakąkolwiek styczność z matematyką wie czym są potęgi. Nauczyciel na pewnym etapie waszego nauczania poinformował was, że cokolwiek podniesione do potęgi 0 jest równe jeden. Bardziej dociekliwi mogli dopytywać dlaczego. Ciężko właściwie pojąć jak coś do zerowej równe jest jeden. Na pierwszy rzut oka całkowicie nielogiczne. Matematyka jednak jak zwykle potrafi zaskoczyć i można pokazać to w bardzo prosty sposób. Zacznijmy sobie od zdefiniowania potęgi.
an = a * a * a *... no i tak n razy. W takim razie jak sensownie wyjaśnić, że a0 = 1?
Najlepiej zobaczyć to na przykładzie. Weźmy sobie liczbę 3. Przykład z liczbą dwa będzie w źródle, chcę pokazać wam, że działa za każdym razem.
31 = 3
32 = 9
33 = 27
34 = 81
35 = 243
Teraz zgodnie z zasadami działań na potęgach tzn. an/ak=an-k
35/31 = 34
34/31 = 33
33/31 = 32
32/31 = 31
31/31 = ...30, a przecież każdy kto skończył 1 klasę szkoły podstawowej wie, że 3/3 = 1
Dla zobrazowania tego użyje znanego wam narzędzia matematycznego zwanego paint.
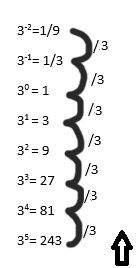
Mam nadzieje, że ta niesamowita wizualizacja pozwoli wam w 100% pojąć skąd wzięła się ta magiczna jedynka. Właściwie jest to banalnie proste, ale nie spotkałem jeszcze nauczyciela na żadnym etapie mojej edukacji (aż do studiów na których aktualnie jestem), który wyjaśniałby regułki, które odgórnie przyjmujemy jako prawdziwe. Dosyć podobnym problemem jest 0!=1, ale to już temat następnego akapitu.
Dlaczego 0!=1?
Pamiętam jak jeszcze w gimnazjum znalazłem jakiegoś mema na którym widniało działanie matematyczne, którego wynikiem było 24 i wywołał ogromne oburzenie w mojej głowie, ponieważ jak byk stało tam 4! w wyniku, a opis mema sugerował, że wynik jest prawidłowy. W ten suptelny sposób dowiedziałem się czym jest silnia i faktu, że człowiek uczy się całe życie. Kończąc tą krótką anegdotę przejdźmy do konkretów. Tak jak w poprzednim przypadku zacznijmy od tego czym właściwie jest silnia. Zgodnie z definicją zaczerpniętą z wikipedii jest to "iloczyn wszystkich liczb naturalnych dodatnich nie większych niż n." Czyli nic innego jak n!=1 * 2 * 3 * 4 *... * n. No i znów nasuwa się pytanie "Dlaczego w takim razie 0!=1?" Sposób dojścia do tego jest całkiem podobny jak w przypadku z potęgami.
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
Korzystając z faktu, że n! / n = (n-1)! mamy:
5! / 5 = 4!
4! / 4 = 3!
3! / 3 = 2!
2! / 2 = 1!
1! / 1 = 0! czyli dokładnie to co mieliśmy wyłożone na tacy przez nauczyciela gdzieś w liceum.
Wizualizacja ze strzałkami:
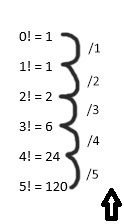
Znów banalnie proste, a jednak dosyć ciekawe. Mam nadzieje, że tej części z was, która tego nie wiedziała, uświadomiłem skąd przyjmujemy właśnie takie wartości. Matematyka jest piękna.
Żart od prowadzącego
Mamy dwa wielomiany :
W1(x) = 3x4 - 4x2 + 7x + 11
W2(x)= 7x3 + 12x - 4
Dlaczego wielomian drugi salutuje wielomianowi pierwszemu?
.
.
.
.
.
Bo W1 jest wyższego stopnia :V
Podsumowanie
Angielskojęzyczne źródło z którego korzystałem
Polecam serdecznie kanał, który posłużył mi za źródło i dla ciekawskich z podstawową wiedzą z angielskiego polecam sposób wyjaśnienia dlaczego nie można dzielić przez 0. Do zobaczenia za parę dni i wesołych świąt wszystkim :)
Mi w szkole też nikt nie wytłumaczył nigdy dlaczego tak jest z tymi potęgami i silnią. Dopiero Ty swoim artykułem otworzyłeś mi oczy :) Teraz to wszystko jasne i jak się okazuje - ma sens! Ciekaw jestem dalszych postów tego typu. Fajnie dowiedzieć się zawsze czegoś nowego!
Congratulations @miszorek! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!