Computation Contest #7 Results and Solution
Solution
The problem of this contest was to test two methods to approximate pi and measure how accurate they get compared to how many digits it gets right.
I wrote a simple code which uses the following two methods:
- Count how many grid dots are in a circle(can be done in linear time when using the circle function).
- Use the following sequence to apprixmate it:
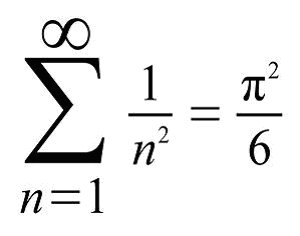
I decided to go with a maximum accuracy of twenty binary digits. Here is my code
import javax.swing.JFrame;
import java.awt.Graphics;
import java.awt.Color;
public class abcd extends JFrame {
int[] firstMethod;
int[] secondMethod;
public abcd() {
setSize(800, 400);
setVisible(true);
doFirstMethod();
doSecondMethod();
repaint();
}
// return accuracy in bits:
public int getAccuracy(double approx) {
if((int)approx != 3)
return 0;
long approxL = Double.doubleToLongBits(approx);
long piL = Double.doubleToLongBits(Math.PI);
long mantissaStart = 0x0008000000000000L;
int prec = 0;
for(long i = mantissaStart; i >= 0; i >>= 1) {
if((approxL & i) != (piL & i))
return prec;
prec++;
}
return prec;
}
public void doFirstMethod() {
firstMethod = new int[20];
int index = 0;
for(int i = 0; index < 20; i += 1+(i>>3)) {
double π = countDots(i);
int numDigits = getAccuracy(π);
if(numDigits >= index+1) {
// Repeat the calculation a couple of times to increase time accuracy
long t1 = System.nanoTime();
for(int j = 0; j < 1000000; j++)
getAccuracy(π);
long t2 = System.nanoTime();
firstMethod[index] = (int)((t2-t1)/1000000.0);
index++;
}
}
}
public void doSecondMethod() {
secondMethod = new int[20];
int index = 0;
for(int i = 0; index < 20; i += 1+(i>>3)) {
double π = sumUp(i);
int numDigits = getAccuracy(π);
if(numDigits >= index+1) {
// Repeat the calculation a couple of times to increase time accuracy
long t1 = System.nanoTime();
for(int j = 0; j < 1000000; j++)
getAccuracy(π);
long t2 = System.nanoTime();
secondMethod[index] = (int)((t2-t1)/1000000.0);
index++;
}
}
}
// Use the partial sums of the infinite sequence sum 1/n² = π²/6:
public double sumUp(int n) {
double sum = 0;
for(int i = 1; i <= n; i++) {
sum += 1.0/i/i;
}
return Math.sqrt(sum*6);
}
// Counts how many grid points lie in-/outside a quarter circle. Kind of similar to integrating the circle function.
public double countDots(int r) {
long num = 0;
long rSqr = r*r;
for(int i = 0; i < r; i++) {
num += (long)(Math.sqrt(rSqr-i*i)); // Use the floor function to find the number of grid points inside the circle at this position.
}
return 4*num/(double)rSqr;
}
public void paint(Graphics g) {
g.setColor(Color.BLACK);
for(int i = 1; i < 20; i++) {
g.drawLine(i*10, 200-firstMethod[i-1], i*10+10, 200-firstMethod[i]);
g.drawLine(200+i*10, 200-secondMethod[i-1], 200+i*10+10, 200-secondMethod[i]);
}
}
public static void main(String[] args) {
new abcd();
}
}
This code outputs the following two graphs:
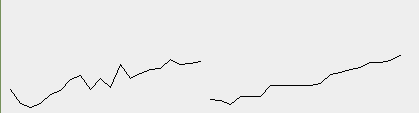
Not much to see except from the fact that both graphs are growing kind of linear.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
List of participants with their entries:
| Name | Solution found | Comment |
|---|---|---|
| @lallo | Integrating the circle function | Strange that your function seems to grow exponentially, while mine are at least on the scale I observed mostly linear. Probably python is doing something strange? |
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Winners:
Congratulations @lallo, you won 2 SBI!
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
A member bonus $trendotoken tip, and !trendovoter, for @quantumdeveloper from MAPXV! These bonuses are for members, selected at random, and last for a few days.
Also consider our MAPR fund and MAXUV vote bonds too.
MAP Steem Fintech: growing your STEEM without SP.
Congratulations @mapxv, you successfuly trended the post shared by @quantumdeveloper!
@quantumdeveloper will receive 4.40698725 TRDO & @mapxv will get 2.93799150 TRDO curation in 3 Days from Post Created Date!
"Call TRDO, Your Comment Worth Something!"
To view or trade TRDO go to steem-engine.com
Join TRDO Discord Channel or Join TRDO Web Site
Congratulations @mapxv, 55.45% upvote has been shared with your successful call on the post that shared by @quantumdeveloper!
Support @trendotoken projects by delegating : 100SP , 200SP , 500SP , 1000SP , 2000SP
A bonus $trendotoken tip from ONECENT!
Also consider MAPR fund and MAXUV vote bonds too.
MAP Steem FinTech: growing your STEEM without SP.
I think in my case it grows exponentially because my algorithm doesn't stop when a certain level of precision is achieved, but it stops after doing n iterations.
So it depends on the input that is exponential. But I'm not sure.
I should modify the algorithm and find the exactly number of iteration and time needed to achieve 1,2,3,4,5,... decimal digits correct. And see if it changes.
Congratulations @quantumdeveloper, your post successfully recieved 4.40698725 TRDO from below listed TRENDO callers:
To view or trade TRDO go to steem-engine.com
Join TRDO Discord Channel or Join TRDO Web Site