Matemática / Dizimas periódicas 2
Post anterior: https://steemit.com/pt/@magalhastudios1/matematica-dizimas-periodicas
Uma outra forma de resolver dizimas periódicas:
No post anterior vimos que para transformar uma dizima composta em fração era necessário seguir este método:
O numerador será o (ante-período seguido do período) - (o ante-período). O denominador será composto de 9s e 0s. A quantidade de 9s será a quantidade de dígitos do período e a quantidade de 0s será a quantidade de dígitos do ante-período.
Mas de onde vem este deste método?
Bem, esse método pode ser facilmente provado;
Dado uma fração composta qualquer do tipo K,AP sendo K um número inteiro qualquer, A o ante-período e P o período.
(K,APPP...)Z = KA,P ; então Z = 10^(nº de algarismos de A)
(K,APPP...)Y = KAP,PPP... ; então Y = 10^(nº de algarismos de A+ nºde algarismos de P)
(KAP,PPP...)-(KA,PPP...) = (KAP)-(KA)
(KAP)-(KA) = (K,APPP...)Y - (K,APPP...)Z
(KAP)-(KA) = (K,APPP...)(Y - Z)
[(KAP)-(KA)]/(Y - Z) = (K,APPP...)
(Y - Z) = [10^(a+p)] - [10^(a)] = [10^(a)][10^(p)-1]
Analisando a equação [10^(a)][10^(p)-1] temos que o termo [10^(p)-1] determina o números de 9 em função de p(algarismos do período) e o termo [10^(a)] determina os números de 0 em função de a(algarismos do ante-período).
Portanto fica provado o método através do numerador que é a parte inteira(K) seguida de ante-período(A) e período(P) diminuída da parte inteira(K) seguida do período(P). O denominador como provado terá 9s igual a quantidade de algarismos do período e de 0s igual a quantidade de algarismos do ante-período.
Exemplos:
712,565656... = 100x
71256,565656... = 10000x
71256,565656... - 712,565656... = 10000x - 100x
70544 = 9900x
x = 70544/9900
(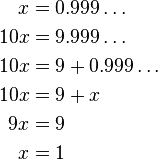 )
)