Flow.

Who hasn't played Flow at least once? Who hasn't killed time with this little game where you connect colored dots with lines? I don't know. I certainly have, and to be honest I've played this simple game more than I'd be willing to admit.

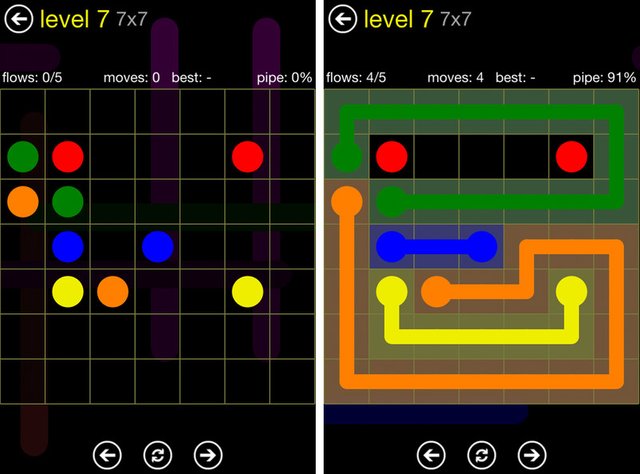
But the fact that it's a simple game doesn't make it easy (ask a Sudoku player!). One day I thought "Hmm... Could I make a simple program to solve Flow puzzles?". Long story short: I never got around to it, but what I did do was something equally fun. A Flow puzzle generator :)

Yeah, that's right. A little Python 3 script that makes a Flow puzzle of any size you want. In this post I'll explain how it works, and how you can do it too. Here it goes.

The Algorithm

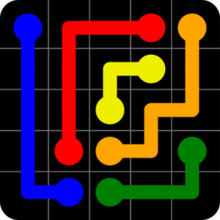
The way it works is really simple. Think of this: what makes Flow complicated is that you must join dots with uninterrupted lines. That is, without one line crossing another. When you're dealing with four, colors solving the puzzle is easy. When you're dealing with twelve... not so much. But this actually gives you an idea of how to make puzzles.

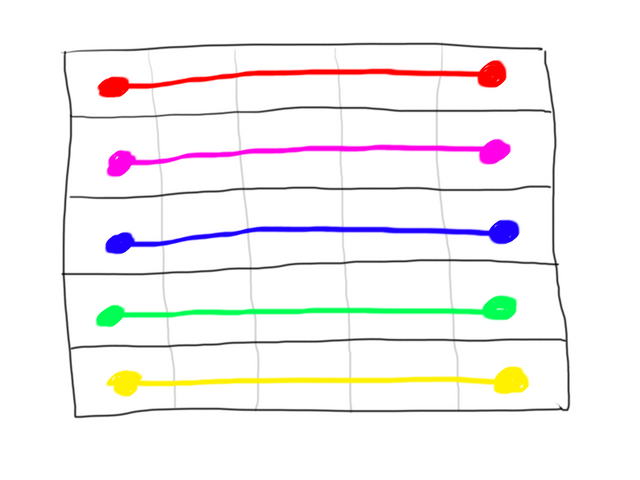
Imagine you have a 5x5 puzzle, with five different colors. In total, there will be five lines connecting the ten dots in a pairwise fashion, according to the dots' color. Now imagine you take those lines and move/stretch them to fit the grid, like this

Surely, there must be one way to go from this configuration to the puzzle we originally had. But how? Let's do it one step at a time. Literally, one grid square at a time :)

If we think about the puzzle's lines, the only two restrictions on them are

• No line may cross another line
• The lines must cover the entirety of the grid (no empty spaces)

Simply put, if we tag the different parts of the line as "tails" and "belly"

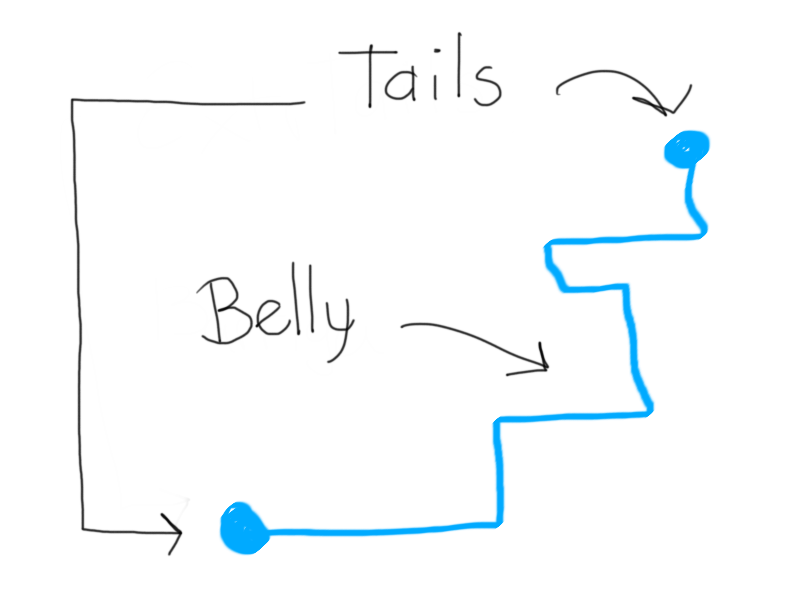
we have the following rule on how me way move the lines about the grid

• No tail can take the place of a belly

Then, as long as we respect that rule, we may drag around, extend or shrink the lines over the grid as we please. But this implies that we can only move tails (that is, we can't just extend a line's belly). We can't change lines in any other way! Furthermore, if we accidentally move a tail into the belly of a line, we'll be breaking our only rule! And this leads us to our final conclusion:

We may only move the tail of any line, and, when we do, we must make room for it by moving the tail of another line as well

That is, two actions must be performed for moving a line

• Analize the grid and say which tails (of different color) share an edge (that is, that are one square away from eachother)

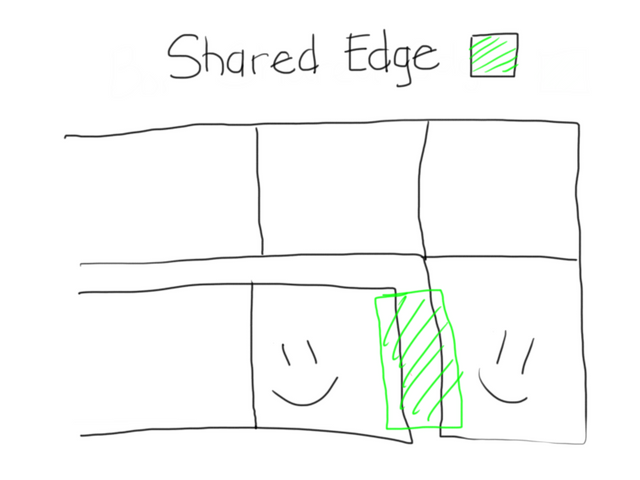
• Extend one line and shrink the other by said tails, the former taking the place left by the latter as it shrinks.

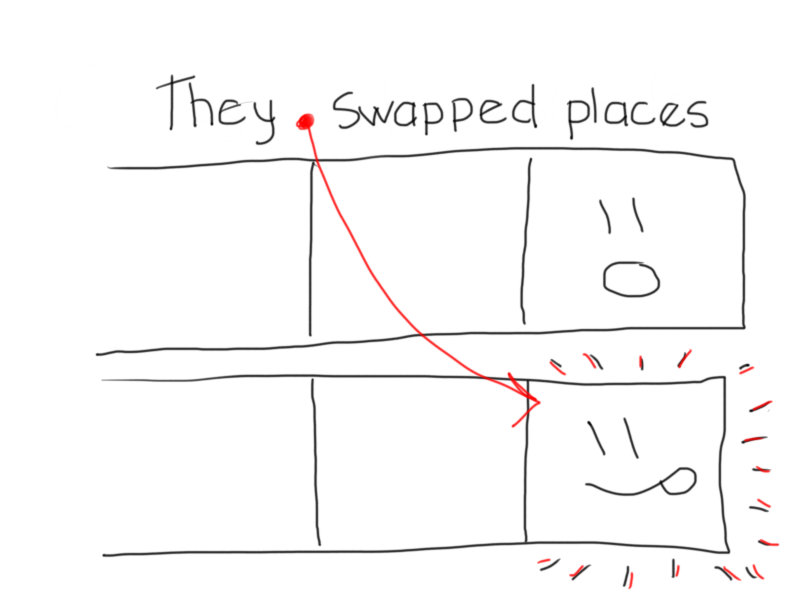
If we do this over, and over, and over again, we eventually reach a tangled mess of lines, sure... but a mess of lines that never cross eachother! And that is a Flow puzzle :)

The Code

Once we have the algorithm in place, the code is surprisingly simple! First things first: let's import the modules


import numpy as np
import random
import colored


We'll use random to generate random numbers and shuffle some things, colored to give color to our results, and numpy just to calculate vector norms (If you're not sure of what I'm talking about, you might want to read this first). Fair warning, though: this code, as it is, runs only on Linux because of the coloredmodule. Apparently, Windows hates making colored fonts appear on their console a pain in the ass. All of the packages I mentioned are either included in your Python distribution or available for download with pip3.

Now, let's define some variables. Here we define our colors, which are actually double spaces (" ") with a changed background color:

re = colored.attr('reset')
na = colored.bg('0') + "  " + re    #The double space is actually really important
a = colored.bg('1') + "  " + re     #it so happens that double spaces look a lot like squares
b = colored.bg('2') + "  " + re     #in the Linux console, so it serves as a nice trick
c = colored.bg('3') + "  " + re     #to make little colored squares. With this, we'll draw the Flow lines
d = colored.bg('4') + "  " + re
e = colored.bg('5') + "  " + re
f = colored.bg('6') + "  " + re
g = colored.bg('7') + "  " + re
h = colored.bg('8') + "  " + re
i = colored.bg('9') + "  " + re
j = colored.bg('10') + "  " + re
k = colored.bg('11') + "  " + re
l = colored.bg('12') + "  " + re
m = colored.bg('13') + "  " + re
n = colored.bg('14') + "  " + re
o = colored.bg('15') + "  " + re
dic = [a,b,c,d,e,f,g,h,i,j,k,l,m,n,o]

Some code & puzzle parameters...

n = 8                               #Grid dimension
chain_limit = n-4                   #Minimum line length
iter = 800                          #Number of iterations

And now, our code's engine. Three important functions: one to generate the initial state of the grid...

def baseMatrix(dim):                #Generates the initial state of the grid with horizontal lines of length 'n'
    A = []                          
    for l in range(dim):
        A.append([])                #Adds 'dim' empty entries in the first level of the list
    for i in range(dim):
        for j in range(dim):
            A[i].append([np.array([i+1,j+1]), dic[i]])              #Fills every level 0 list with the line's informatio:
                                                                    #XY coordinates of each point on the line, as well as a tag indicating the line's color                                                                 #The beginning and end of this list are the line's tails
                                                                    #Selecting a list from 'A' is the same as selecting a whole line
    return A

... another one to actually make the tails extend/shrink...

def edgeSwitch(A):                  #Most important code of this generator: this function extends/shrink two lines whose tails share an edge                                    #First, it analyzes every line:
    sw = False
    for i in range(len(A)):                         #For each row (that is, for every line)...
        if sw == True:
            break
        for k1 in range(-1,1):                      #For every tail of the selected line...
            if sw == True:
                break
            p = A[i][k1][0]                         #where 'p' is the position of the selected tail...
            for j in range(len(A)):                 #For all the other lines...
                if sw == True:
                    break
                if j == i:
                    continue
                if len(A[j]) == chain_limit:        #with length greater than 'chain_limit'...
                    continue
                for k2 in range(-1,1):              #For every tail of the second line...
                    if sw == True:
                        break
                    pprime = A[j][k2][0]            #where'pprime' is the position of the seond line's tail 
                    if np.linalg.norm(p-pprime) == 1.0:                 #If the distance between both positions is exactly one, then they share an edge.
                        n1 = np.random.rand()                           #We flip a coin, and if 'n1' is greater than 0.5...
                        if n1 > 0.5:
                            A[j].pop(k2)                                #We remove the second line's tail...
                            if k1 == -1:
                                A[i].append([pprime,A[i][0][1]])        #... and add it to the first one.
                            elif k1 == 0:
                                A[i].insert(0,[pprime,A[i][0][1]])
                            sw = True
                    else:
                        continue                                        #If 'n1' is not greater than 0.5, we simply continue with another (second) line 
    return A

... and two final functions to, well, see the puzzle (and its solution :P)

def flowPrinter(A):                 #An auxiliary function for printing the puzzle
    C = []                          #We make an empty list...
    for z in range(n):
        C.append([na]*n)            #... and fill it with n' sublists of 'n' entries whose content is a black double space ('na' is black, according to our color definition)
    for i in range(len(A)):
        for j in range(len(A[i])):              
            x = A[i][j][0][0] - 1               #We find the indices of each line element...
            y = A[i][j][0][1] - 1               
            C[x][y] = A[i][j][1]                #... and overwrite that element in 'C' with the appropriate color
    s = ""
    for k in range(n):                          #Finally, we print every line of  'C' as a single string.
        for l in range(n):
            s = s + C[k][l]
        print(s)
        s = ""
def flowPrinter_puzzle(A):
    C = []
    for z in range(n):
        C.append([na]*n)
    for i in range(len(A)):
        for j in range(-1,1):
            x = A[i][j][0][0] - 1
            y = A[i][j][0][1] - 1
            C[x][y] = A[i][j][1]
    s = ""
    for k in range(n):
        for l in range(n):
            s = s + C[k][l]
        print(s)
        s = ""

Now, all we have to do is write tha main loop:

flow = baseMatrix(n)
for step in range(0,iter):
    flow = edgeSwitch(flow)
    random.shuffle(flow)
flowPrinter(flow)
print('\n \n')
flowPrinter_puzzle(flow)

Caution: that random.shuffle(flow) is SUPER important. SinceedgeSwitch has to go by every row of A in a descending fashion, the algorithms gives a certain priority to the first rows. With that piece of code we shuffle the ordering of the rows in A, but not their contents, thus eliminating this priority.

And that's it. That is truly all there is to it. With around 140 lines of code we've managed to make a script that generates Flow puzzles of arbitrary size :) Now let's run it and see the results!

Results

Running python3 flowgen.py (that's how I called it) forn=15, we get a random 15x15 Flow puzzle :)

Switching up n=8 and taking iter=400we get an 8x8 puzzle.

Even if those greens and reds look alike, they're not! It's a matter of image processing for the Steemit post. Sorry :(

And finally, a 6x6 one just for giggles (c'mon, 4x4 ones are just plain trivial).

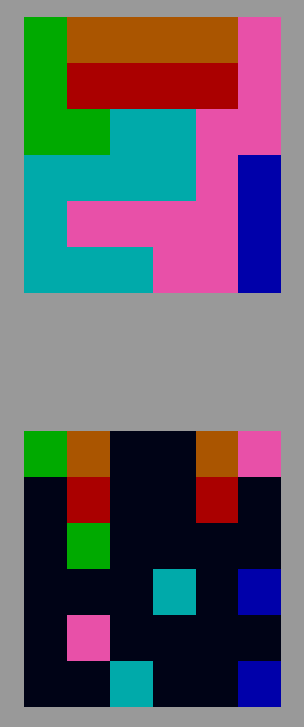
Remarks and Comments

The first time I ran this code, I noticed something. If iteris too big, you'll have a problem: you'll just get a bunch of colored rectangles. If this is the case with iter, more often than not a tail will get stuck between another lines belly and its own belly, or its other tail, making a nice rectangle that runs around itself forever. The solution to this is simply choosing a suitable value for iter; I've found that taking iter = 10*nworks good enough in making a tangled mess. Also, if you don't pay attention to chain_limityou'll most likely get a trivial line (whose belly only has one square, or has no belly at all). And that's certainly undesirable: you want an intricate, almost evil, mess >:) One final comment: you can make the puzzles as big as you want, but keep in mind that you'll most likely run out of colors (or have so many that you won't be able to distinguish them!). If you really want to go that far, just change dic's definition to alphabet letters. You wont have colors anymore, but you'll be able to make a 26x26 puzzle!

I hope you liked this post, that you learned something, and, above all else, that you leave this feeling you could've invented Flow yourself :)

If you'd like me to make more programming posts like this one, follow me, send me an upvote with your best wishes, and leave a comment below letting me know what you think :)

See you around,

-SA

---

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.