unsplash.com

Dear Steemian...

Tahukah kalian Algoritma Genetika pada dasarnya ialah ilmu pencarian solusi yang diilhami oleh proses genetika. Karena itu istilah yang digunakan dalam algoritma ini banyak diadaptasi dari ilmu tersebut. Pada algoritma ini, teknik pencarian dilakukan pada mekanisme seleksi alamiah. Dengan kata lain, algoritma genetika merupakan suatu teknik pencarian acak yang mempertahankan sejumlah solusi untuk masalah yang akan ditangani. Dimana poin iteratif baru dalam ruang pencarian yang dihasilkan untuk evaluasi dan opsional dimasukkan ke dalam populasi (Smith, 2002).

Permasalahan umum pada algoritma genetika adalah lokal optimum yang terjadi karena hilangnya perbedaan populasi (population diversity) awal dengan selanjutunya (Zhu & Liu, 2004). Jika perbedaan populasi terlalu kecil maka memungkinkan terjadinya lokal optimum, dan jika terlalu besar maka mengakibatkan lamanya waktu yang dibutuhkan untuk menghasilkan solusi terbaik. Permasalahan ini dapat diselesaikan dengan menambahkan proses elitisme dimana proses ini akan menyelamatkan populasi terbaik pada tiap generasi. Populasi tersebut akan disimpan dan dibandingkan kepada populasi terbaik pada generasi berikutnya. Jika populasi yang dibandingkan lebih baik dari populasi sebelumnya, maka nilai pada populasi elitisme akan digantikan dengan populasi baru. Jika sebaliknya, maka populasi elitisme akan dipertahankan untuk ke generasi berikutnya lagi. Proses ini akan berulang hingga akhir dari generasi.

Algoritma genetika yang dikembangkan untuk permasalahan knapsack problem dengan menjaga sekumpulan kromosom-kromosom terbaik sehingga perlahan-lahan solusi terbaik dapat dicapai (Haibo et al, 2011). Penentuan jumlah mutasi yang tepat akan memberikan dampak pada cepat tidaknya suatu solusi ditemukan. Mutasi dinamis adalah metode yang dapat diterapkan pada penelitian ini. Pada mutasi ini, tingkat mutasi bergantung pada hasil fitness dari suatu generasi. Semakin banyak fitness yang mendekati kepada nilai solusi, maka semakin sedikit jumlah gen pada tiap populasi yang akan salaing bermutasi dan begitu juga sebaliknya.

Permasalahan Knapsack adalah suatu permasalahan optimasi kombinatorial. Sebagai contoh, diberikan satu set item dengan berat dan nilai, kemudian dilakukan pemilihan dari item-item tersebut untuk dimasukkan ke dalam tas dengan kapasitas terbatas. Jadi, item-item yang dimasukkan beratnya harus lebih kecil atau sama dengn kapasitas dari ransel tersebut, tetapi total nilai sebesar mungkin (Singh, 2011).

Knapsack problem dapat menentukan bobot yang diinginkan pada suatu ruang pencarian. Knapsack sendiri memiliki setidaknya dua parameter sebagai penentu apakah fitness dari suatu populasi mendekati dengan solusi yang ditentukan sebelumnya. Parameter yang dipakai pada penelitian ini adalah jumlah node dan bobot jarak. Jumlah node merupakan jumlah titik koordinat yang akan dilalui sementara bobot jarak adalah jumlah akumulasi jarak antar node hingga kembali ke node asal. Pada algoritma ini diharapkan solusi yang dicapai dapat menghasilkan fitness = 1 atau setidaknya mendekati ke angka tersebut.

Pada kasus Travelling Salesmen Problem, dimana algoritma genetika harus mencari solusi dari semua node yang dilalui dan mencari nilai paling optimal atau jalur terpendek yang dilalui pada lintasan tersebut. Algoritma genetika dapat mencari solusi yang optimal pada setiap generasi yang dilaksanakan tetapi hasil tersebut bukan merupakan jawaban yang paling benar untuk mencari jarak diinginkan. Oleh karena itu saya akan melakukan beberapa penelitian tentang bagaimana menerapkan teknik mutasi dinamis pada algoritma genetika lalu dapat mencapai hasil analis yang akan dipelajari selanjutnya. Maka langsung saja simak beberapa pembahasan berikut ini.

METODOLOGI

Pada algoritma genetika, penentuan operator mutasi yang dipengaruhi oleh nilai mutasi merupakan hal yang sangat penting, karena akan memberikan solusi yang optimal. Penentuan nilai mutasi secara dinamis diharapkan dapat menghindari local optimal dan mempercepat penemua solusi dari permasalahan karena perubahannya bisa dikontrol.

Rancangan Penelitian

Dalam penelitian ini akan dilakukan tahapan berurut secara keseluruhan untuk menyelesaikan masalah. Adapun tahapan penyelesaian tersebut terlihat pada gambar 1 berikut :

Gambar 1. Skema Penyelesaian Masalah

Rancangan Genetika

Pada bagian ini akan dijelaskan bagaimana algoritma genetika mengambil peranan dalam proses optimasi pada pencarian lintasan. Dalam mencari lintasan ada beberapa hal yang penting untuk dipertimbangkan yaitu bobot dan jumlah lintasan. Pada metode yang diterapkan pada penelitian ini lintasan yang dicari bukan sepenuhnya dari total lintasan melainkan sebahagian saja tergantung dari input yang diinginkan. Jumlah lintasan yang dicari tidak melebihi dari total lintasan.

Gambar berikut ini menjelaskan contoh proses pencarian lintasan dari total lintasan yang ada.

Gambar 2. Contoh lintasan dengan 10 buah node

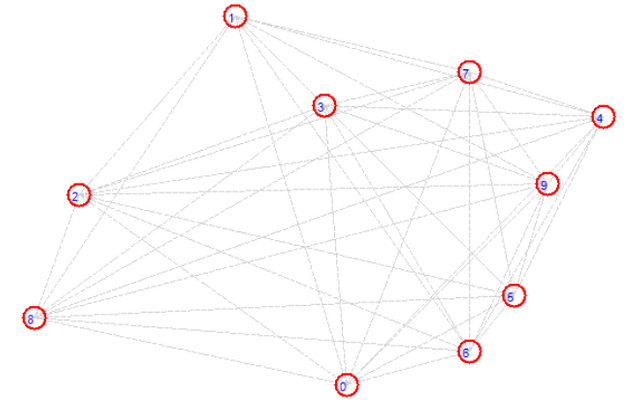
Pada gambar di atas dapat dilihat sebuah pola lintasan dengan 10 buah node yang terdiri dari titik 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Setiap node akan dibentangkan pada koordinat 2 dimensi yang titik origin (0, 0) berada pada sudut kiri atas. Tabel di bawah ini kan memerikan keterangan tetang posisi koordinat setiap note pada sumbu X dan sumbu Y.

Tabel 1. Data koordinat lintasan

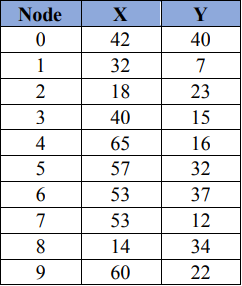
Pada Tabel 1 ada 10 buah posisi koordinat. Setiap node memiliki pasangan sumbu X dan sumbu Y. Seperti contoh, pada node ke 5 memiliki sumbu X = 57 dan sumbu Y = 32.

Jarak Lintasan

Untuk menentukan lintasan mana yang memiliki nilai optimal yang terbaik. Jarak yang dipergunakan untuk menentukan posisi lintasan mana yang memiliki nilai paling optimal yaitu dengan cara menentukan jumlah lintasan mana yang paling mendekati bobot yang diinginkan. Pencarian jarak ini berbeda dengan jarak pada kasus TSP pada umumnya. Pada kasus umum, jarak akan menghitung bobot setiap node, tetapi pada permasalahan Knapscak, jarak dicari berdasarkan jumlah node yang dinginkan saja dan perkisaran bobot tertentu. Jarak dapat dihitung pada rumus berikut ini.

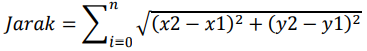
Pengambilan lintasan tidak boleh mempunyai node yang berulang kecuali node awal dan node akhir karena setiap node hanya dapat disinggahi cuma sekali saja. Sebagai contoh, akan diambil sebuah buah lintasan dengan 5 buah node:

Lintasan = 2 – 6 – 9 – 4 – 2

Jarak 1 = 2 – 6

Jarak 2 = 6 – 9

Jarak 3 = 9 – 4

Jarak 4 = 4 – 2

To be continued ...

Wondering How Steemit Works, Read Steemit FAQ?