Implementasi Algoritma Genetika Menggunakan Teknik Mutasi Dinamis Knapsack Problem [Part 2]

Dear Steemian...
Pembahasan ini merupakan lanjutan dari pembahasan sebelumnya yang menjelaskan mengenai pengimplementasian pada algortima genetika dalam menggunakan teknik mutasi dinamis Knapsack Problem. Tujuannya ialah demi menghasilkan hasil yang dapat di analisis sebagai bahan pembelajaran dalam mempelajari ilmu-ilmu baik dibidang algoritma genetika maupun algoritma lainnya. Maka langsung saja simak beberapa pembahasan berikut ini.
Node pertama adalah dimana mulai dilakkan perjalanan dan akan berakhir di node kelima dimana node tersebut adalah node yang pertama disinggahi sebelumnya. Setelah diperoleh masing-masing persinggahan, akan dihitung jarak masing-masing persinggahan dan kemudian dijumlahkan semuanya. Ada 4 buah jarak yang harus dihitung untuk setiap 5 node yang disinggahi. Penjelasan berikut akan menjelaskan nilai yang diperoleh dari masing-masing persinggahan.





Dari perhitungan di atas dapat ditentukan nilai dari total jarak yang ditempuh dari mulai lintasan 2 ke 6 sebesar 36.61967, 6 ke 9 sebesar 16.55295, 6 ke 9 sebesar 7.81025 dan 4 ke 2 sebesar 47.51842 adalah sebesar 109.503 berdasarkan rumus pada jarak sebelumnya. Proses ini akan berulang jika ada beberapa lintasan yang kan dicari nilai jaraknya.
Populasi
Populasi akan dibangkitkan sesuai dengan jumlah yang diinginkan. Tidak ada batasan jumlah pembangkitan populasi. Semakin banyak populasi yang dibangkitkan, semakit banyak peluang terciptanya optimum global. Tetapi perlu diperhatikan semakin banyak populasi akan memperlambat proses genetika. Akan tetapi jika kecepatan komputer yang digunakan memadai, dapat dicoba untuk menambahkan jumlah populasi yang dibangkitkan. Sebagai contoh dapat dilihat pada Tabel 2, pada tabel ini akan diujicoba perhitungan bobot target = 400 dan jumlah populasi = 20.
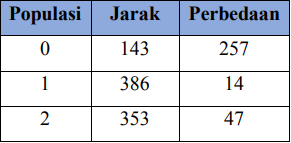
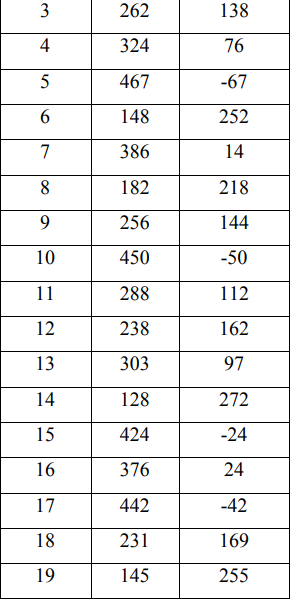
Pada kasus Knapsack, lintasan terpendek bukan berarti terbaik kerena pada model optimasi Knapscak, ada yang namanya bobot target dimana ini merupakan batas dimana nilai jarak harus paling medekati dengan nilai yang tercantum pada bobot target dan tidak melebihi dari nilai tersebut. Angka minus yang tertera di tabel tersebut terjadi akibat nilai jarak melebih dari nilai target yang ditentukan. Nilai yang paling mendekati target berada pada populasi 1 dan 7 dimana perbedaannya adalah 14.
Fitness
Populasi akan proses genetika diharapkan mampu untuk membuat perbedaan mencari nilai 0. Jika nilai perbedaan adalah 0 maka fitness dari populasi tersebut bernilai 1. Perbedaan nilai antara panjang lintasan dan bobot target merupakan Error Code. Jika Error Code menghasilkan 0 berarti secara otomatis fitness akan bernilai 1. Ini dapat diketahui melalui rumus berikut.
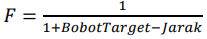
Di bagian ini akan diambil lima buah contoh dari Tabel 2 yaitu populasi 1, 6, 10, 15 dan 19. Di sini akan dibandingkan populasi mana yang mempunyai fitness lebih tinggi dari beberapa populasi yang ditentukan. Akan ada kemungkinan beberapa populasi memiliki nilai yang sama.


Dari perhitungan di atas dapat dilihat nilai fitness mempunyai hasil yang berbedabeda. Pada dasarnya nilai fitness pada suatu proses genetika dapat ditentukan semakin kecil lebih baik atau semakin besar lebih baik. Hal tersebut tergantung pengolahan dan penentuan rumus untuk mencari nilai fitness sebelumnya. Tabel perbandingan nilai ini dapat dilihat pada Tabel 3 berikut ini.
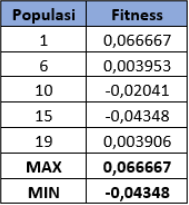
Pada tabel di atas dapat dilihat perhitungan masing-masing populasi. Populasi yang memiliki fitness tertinggi berada pada Populasi 1 yang mempunyai nilai fitness = 0,066667 sementara populasi yang memiliki nilai paling rendah berada pada Populasi 15 yang memiliki nilai sebesar -0,04348. Perhitungan fitness ini akan berulang sebanyak generasi yang ditentukan. Biasanya, perhitungan populasi dilakukan di awal proses dan di akhir proses. Apabila perhitungan fitness pada awal proses sudah menghasilkan solusi dari permasalahan, maka algoritma genetika tidak diteruskan dan hasil akan ditampilkan langsung tetapi ini jarang sekali terjadi nilai sudah optimal pada saat pertama sekali perhitungan dilaksanakan.
Seleksi
Pada tahap seleksi, proses genetika akan melakukan duplikasi populasi yang dianggap baik untuk dijadikan peluang terhadap generasi berikutnya. Untuk mengetahui lebih lanjut mengenai proses seleksi pada metode ini, dapat dilihat pada penjelasan berikut ini.
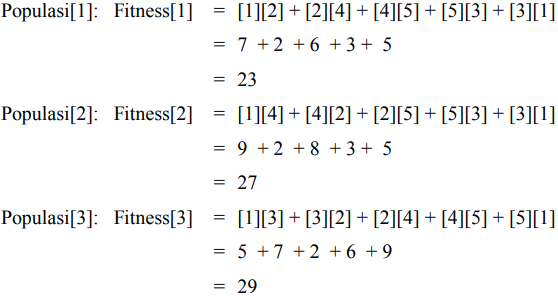

Perhitungan di atas merupakan hasil dari panjang lintasan dari tiap-tiap node yang dilalui. Setiap populasi mempunyai urutan yang berbeda-beda. Ini disebabkan pada saat pembangkitan populasi, angka yang dipergunakan bersifat acak. Total fitness merupakan penentu dari nilai probabilitas dari setiap fitness. Total fitness dapat dicari dengan menggunakan rumus berikut ini.
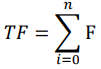
Dengan populasi sebanyak enam buah di atas, maka dapat diperoleh nilai total fitness (TF) adalah:
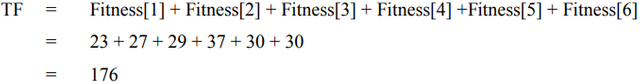
Total fitness tersebut digunakan untuk mencari probabilitas tiap populasi. Pencarian probabilitas dilakukan dengan cara membandingkan hasil fitness dari tiap populasi terhadap nilai total fitness sebagaimana yang digambarkan pada rumus mencari probabilitas berikut ini.
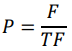
Berdasarkan rumus diatas, akan dilakukan perhitungan probabilitas dari tiap-tiap fitness yang telah diperoleh sebelumnya. Di bawah ini akan dijelaskan perhitungan untuk mencari probabilitas tersebut.
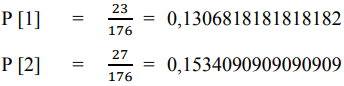



Wondering How Steemit Works, Read Steemit FAQ?

