Implementasi Algoritma Genetika Menggunakan Teknik Mutasi Dinamis Knapsack Problem [Part 3]


Dear Steemian...
Pembahasan ini merupakan lanjutan dari pembahasan sebelumnya yang menjelaskan mengenai pengimplementasian pada algortima genetika dalam menggunakan teknik mutasi dinamis Knapsack Problem. Tujuannya ialah demi menghasilkan hasil yang dapat di analisis sebagai bahan pembelajaran dalam mempelajari ilmu-ilmu baik dibidang algoritma genetika maupun algoritma lainnya. Maka langsung saja simak beberapa pembahasan berikut ini.
Sebelum berada pada tahapan seleksi, maka harus dicari terlebih dahulu probabilitas kumulatif pada tiap-tiap populasi. Probabilitas ini bertujuan sebagai nilai pembanding dari nilai acak yang dibangkitkan oleh proses genetika sebagai acuan populasi mana yang akan terpilih menjadi duplikasi. Populasi yang terpilih akan menduplikatkan dirinya kepada populasi yang aktif sehingga kemungkinan besar akan ada beberapa populasi yang memiliki nilai-nilai gen yang sama.
Untuk mencari nilai probabilitas pada tiap-tiap populasi dapat dilakukan dengan rumus seperti di bawah ini.
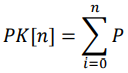
Berdasarkan rumus di atas, akan dicari nilai dari probabilitas kumulatif pada tiap-tiap populasi. Perhitungan nilai ini dapat dilihat dari penjelasan di bawah ini.

Dalam mencari nilai probabilitas kumulatif ada beberapa hal yang perlu diperhatikan agar nilai tersebut tidak salah. Kelemahan dari proses genetika salah satunya adalah jika ada rumus yang salah, maka perlu penelusuran dari awal untuk mencari letak kesalahaan perhitungn tersebut. Pada probabilitas komulatif dapat kita lihat bahwa nilai PK[1] pasti akan selalu sama dengan nilai P[1] dan nilai PK[n] selalu bernilai dengan 1. Jika kedua bagian ini tidak benar, maka sudah dipastikan dalam proses pencarian nilai probabilitas kumulatif tidak mengikuti aturan yang sebenarnya.
Proses seleksi yang dipakai pada metode ini adalah metode Roulette Wheel. Proses seleksi membangkitkan bilangan acak yang berada antara 0 dan 1 pada setiap populasi dan kemudian nilai tersebut akan dibanding kan dengan nilai probabilitas komulatif dengan syarat PB[n-1] < R[n] < PB[n]. Berikut penjelasan untuk mencari proses seleksi.
Nilai Acak Populasi [1] adalah R[1] = 0,314
Nilai Acak Populasi [2] adalah R[2] = 0,111
Nilai Acak Populasi [3] adalah R[3] = 0,342
Nilai Acak Populasi [4] adalah R[4] = 0,743
Nilai Acak Populasi [5] adalah R[5] = 0,521
Nilai Acak Populasi [6] adalah R[6] = 0,411






Proses seleksi pada populasi menyebabkan ada beberap dari populasi yang mengalami perubahan dan duplikasi dari populasi yang lainnya. Di bawah ini akan ditampilkan populasi sebelum dan setelah proses seleksi Roulette Wheel.

Setelah proses seleksi, ada dua buah populasi yang mengalami duplikasi yaitu Populasi[1] dan Populasi[6]. Nilai baru yang dimasukkan ke populasi ini berasal dari Populasi[3] sehingga Populasi[1], Populasi[3] dan Populasi[6] memiliki nilai yang sama. Sementara Populasi[2] bertukar ke Populasi[4], Populasi[4] dengan Populasi[5] dan Populasi[5] dengan Populasi[4].
Mutasi
Proses mutasi yang digunakan adalah mutasi dinamis dimana nilai mutation ratenya tergantung dengan keadaan satu generasi. Jika dalam satu generasi ada banyak nilai fitness yang mendekati ke target, maka persentase mutasi akan semakin semakin sedikit dan sebaliknya apabila nilai-nilai fitness pada generasi tersebut jauh dari target, persentase mutasi akan lebih besar.
Sebagai contoh ada 10 buah populasi yang terbagi tiga bagian yaitu Rendah, Sedang dan Tinggi. Pada hasil fitness sebelum mutasi akan dilakukan pengujian fitness mana saja saja yang mendekati kepada target. Nilai keluaran dari perhitungan tersebut menjadi nilai yang digunakan sebagai mutation rate.
Pada perhitungan berikut ini akan dijelaskan cara perhitungan secara dinamis untuk menentukan nilai mutation rate dari proses genetika. Contoh ini mempunyai sepuluh buah populasi setelah proses seleksi dimana setiap populasinya mempunyai lima buah node yang disinggahi.Data di bawah ini diambil dari perhitungan penjumlahan jarak lintasan yang dilalui. Setiap populasi memiliki nilai yang berbeda. Nilai tersebut akan dibandingkan dengan target yang telah ditentukan. Nilai yang lebih mendekati kepada target memiliki peluang besar untuk dijadikan sebuah solusi. Nilai yang melebihi dari 1 tidak dapat divalidasi karena telah melebihi dari target yang ditentukan. Solusi dari permasalahan hanya boleh berada diantara nilai target dan nilai yang berada dibawahya.
Populasi[1] = [1][2] + [2][4] + [4][5] + [5][3] + [3][1]= 23
Populasi[2] = [1][4] + [4][2] + [2][5] + [5][3] + [3][1]= 27
Populasi[3] = [1][3] + [3][2] + [2][4] + [4][5] + [5][1]= 29
Populasi[4] = [1][5] + [5][2] + [2][3] + [3][4] + [4][1]= 37
Populasi[5] = [1][5] + [5][3] + [3][2] + [2][4] + [4][1]= 30
Populasi[6] = [1][3] + [3][4] + [4][5] + [5][2] + [2][1]= 30
Populasi[7] = [1][4] + [4][2] + [2][5] + [5][3] + [3][1]= 21
Populasi[8] = [1][3] + [3][2] + [2][4] + [4][5] + [5][1]= 33
Populasi[9] = [1][5] + [5][2] + [2][3] + [3][4] + [4][1]= 44
Populasi[10] = [1][5] + [5][3] + [3][2] + [2][4] + [4][1]= 35
Selain nilai jarak lintasan ada namanya bobot target. Pada kasus ini akan ditentukan bobot target sebesar 40. Diperlukan suatu perhitungan probabilitas untuk menentukan kemungkinan peluang suatu populasi terpilih untuk mempengaruhi mutation rate.
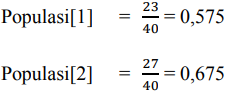

Jika diambil batas rentang sebesar 75%, maka yang masuk nominasi diantara populasi tersebut adalah Populasi[5], Populasi[6], Populasi[8] dan Populasi[10]. Populasi[9] tidak akan pernah terpilih karena memiliki nilai diatas 1. Jadi ada 4 buah yang akan diolah pada perhitungan mutation rate.
Rumus untuk mencari mutation rate adalah seperti yang terlihat di bawah ini.
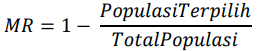
Sehingga dapat dihitung nilai mutation rate adalah:
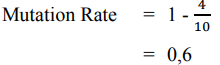


Wondering How Steemit Works, Read Steemit FAQ?


Thanks for using eSteem!
Your post has been voted as a part of eSteem encouragement program. Keep up the good work! Install Android, iOS Mobile app or Windows, Mac, Linux Surfer app, if you haven't already!
Learn more: https://esteem.app
Join our discord: https://discord.gg/8eHupPq