Calculating the relative position between two planes given in parametric form
Hi everyone :)
If we look at a three-dimensional coordinate system, the following relative positions between two planes can occur:
(A short explanation for those who don't know what a plane in geometry is, imagine it as flat, 2 dimensional thing that extends infinitely far (the reason why planes can't be skew like we know it from skew lines). You can simply make one by yourself, choosing a random vector, let's say (1/2/3) and two more different vectors like (3/5/6) and (4/1/2). The equation for the plane would look like this: (1/2/3) + x * (3/5/6) + s * (4/1/2). Voilà. )
The green and blue plane are parallel to each other while the red one cuts the blue and the green one. The third case which we can't really see in this graphic is the case where the planes are identical what would mean the green, blue and red one would have a plane right at the same position. We can see this better inthe following picture, illustrating it at the bottom.
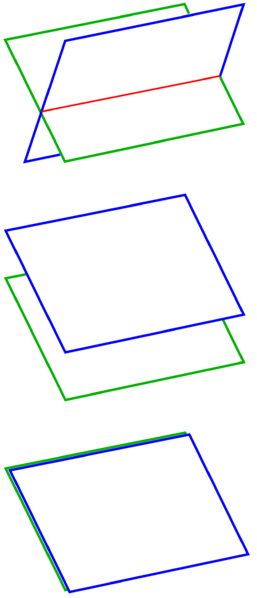
Case 1: Intersection Case 2: Parallelism Case 3: Equality (All vectors of equation 2 are n* times the same as in equation 1)
If we now want to look at how we can calculate the relative position between two planes, we need two equations. One for plane nr.1 and one for plane nr.2.
As an example we take
P1 (2/2/2) + r * (1/0/0) + s * (0/1/0)
P2 (-2/-4/6) + t * (2/1/0) + b * (1/2/0)
Now we have two equations in the parameter form
We can se they aren't identical as their vector products aren't co-linear. To check if they are parallel, simply form the vector product of the two. If you didn't know already, there is a simply trick to do this:
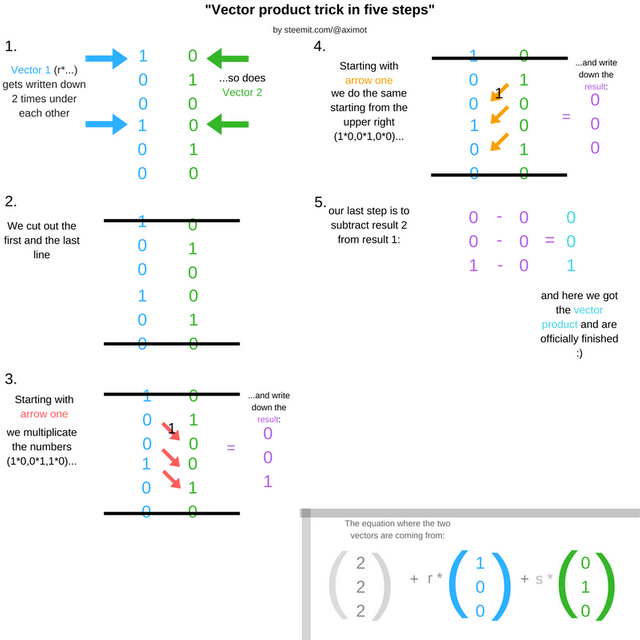
after we are finished calculating the vector product of plane 1 we calculate it from plane 2. Comparing them to each other, we see they are equal. If the vector product of two planes is = n * (a/b/c), they are parallel to each other. You can see this in the first picture as the vector product is the orthogonal arrow upwards from the green and the blue line which are parallel to each other.
If there is no parallelism and neither they are equal, they have an intersection, seen as the red line on the blue plane in picture 1. The intersection is an straight line, which we can determine by the following method:

Turning one equation into a cartesian equation makes it easy for us to just put in equation nr.2 and get our result quickly. Another approach would have been to set the equation 1 = equation 2 and solve the linear equation system. If you want to, I can make a post about this approach too, but for now
Thanks for reading and have a nice day :)
SourceTexthttps://en.wikipedia.org/wiki/Plane_(geometry)https://www.mathebibel.de/parameterform-in-koordinatenform (translated) Ernst Klett Verlag, Lambacher Schweizer Seite 266 ( 1.Auflage) (translated)Pictureshttps://upload.wikimedia.org/wikipedia/commons/thumb/5/56/Proj-ebene-hom-koord.png/800px-Proj-ebene-hom-koord.pnghttps://upload.wikimedia.org/wikipedia/commons/thumb/f/f6/Lage-ebene-ebene.png/257px-Lage-ebene-ebene.png Picture 3 was getting designed with Canva.comPicture 4 was getting designed with Canva.com