Quantum Digital Signatures
Introduction
This is an essay explaining a quantum digital signatures. It's assumed that the reader has the basic understanding of quantum computing - what are qubits, what is superposition, the basic properties of qubits, and, of course, a good grasp of mathematics (one thing you might be unfamiliar with is the bra-ket notation. If there's some interest, I might try explaining the fundamentals of quantum computing in the next post. I'm rather rusty on this topic - this was an essay that I wrote in 2014 for university.
Figure 1. bra-ket notation.
Background
Digital signature is much like a handwritten signature. Its purpose is to show authenticity of a message. In addition to this, digitally signed message also holds the property of non-repudiation, which means that the sender can’t deny having sent this message. Just like in the real world, one would find it hard to deny having signed a contract when there’s a physical copy of the contract with one’s signature.
Classical digital signature is a binary string - usually a hash of a message encoded using a private key (which is known only by the sender). Receiver can decode it using sender’s public key, compute the hash by themselves and see if these two results match. If they do, it’s a strong indication that the message has not been tampered with and is indeed sent by the alleged sender. The scheme relies on the fact that there exist one-way functions, that are exponentially hard to invert - it is easy to get output from input, but nearly impossible to get input given output. An example of such functions would be multiplication of very large numbers (multiplying is easy, factoring is hard). However, factoring is disproved to be an unfeasible task, since one could have a quantum computer and use the Shor’s algorithm to factor large numbers. And while there is no quantum computer big enough for real life purposes, there also seem to be no roadblocks that would prevent it from being possible in the near future.
Quantum Digital Signature Protocol
There are a few quantum digital signature protocols developed. I will try to explain the first protocol by Daniel Gottesman and Isaac L. Chuang.
In this protocol we make a signature from using a message rather than the hash of it (as is often the case in real life classical digital signature implementations).
Alice
Alice wants to send a message to Bob. She is a sender.
Alice signs her message, bit by bit. For each bit 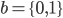 she has to generate a set of pairs of private keys:
she has to generate a set of pairs of private keys: 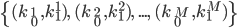
Each  is a classical bit string of length
is a classical bit string of length 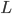 . Keys
. Keys 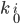 are used if bit
are used if bit 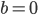 and
and 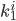 if
if 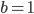 . Value
. Value 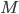 is a security parameter. Security increases with
is a security parameter. Security increases with 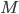 but large
but large 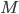 requires more resources (most importantly, more qubits).
requires more resources (most importantly, more qubits).
From these private keys Alice generates a set of public keys. She does that using the function (which is known for all parties of communication) 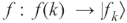 that maps classical bit strings into quantum states. This function is a one-way function because
that maps classical bit strings into quantum states. This function is a one-way function because 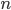 qubits are used for the state
qubits are used for the state 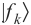 and
and 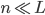 for large enough
for large enough 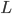 . The latter is the case because the state of
. The latter is the case because the state of 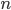 qubits is generally expressed by:
qubits is generally expressed by:
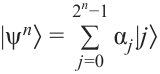 where
where 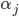 is a coefficient and
is a coefficient and 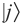 is a basis state.
is a basis state.
It becomes apparent that the number of coefficients in a multiple qubit state increases exponentially with 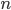 . However, given the public key the most one can do to learn something about
. However, given the public key the most one can do to learn something about 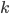 is to measure each qubit individually (Holevo’s theorem), in which case,
is to measure each qubit individually (Holevo’s theorem), in which case, 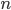 bits would be learned. Alice needs to be aware, though, that all the public keys she produces for a single private key, leak
bits would be learned. Alice needs to be aware, though, that all the public keys she produces for a single private key, leak 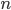 bits of information each, so if she produces
bits of information each, so if she produces 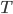 copies and adversary collects them all they may learn
copies and adversary collects them all they may learn 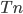 bits about the private key. Therefore, it must be the case that
bits about the private key. Therefore, it must be the case that  . So if Alice wants to produce lots of copies of the public key she’s better off using longer private keys (larger
. So if Alice wants to produce lots of copies of the public key she’s better off using longer private keys (larger 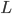 ).
).
Bob
Recipient of Alice’s message is Bob. Bob got the public keys from Alice (will be explained later). Now he gets a message from Alice. The message is made of the message bit 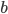 and private keys that were used to create the public keys. Since Bob knows the function
and private keys that were used to create the public keys. Since Bob knows the function 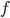 that was used, he can create an identical public key himself, and compare it with the one he got from Alice. The comparison between 2 quantum states can be done using a swap test. If both states are the same, test returns
that was used, he can create an identical public key himself, and compare it with the one he got from Alice. The comparison between 2 quantum states can be done using a swap test. If both states are the same, test returns 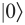 , but if they are different (nearly orthogonal) it might return either
, but if they are different (nearly orthogonal) it might return either 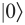 or
or 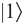 . This is why security parameter
. This is why security parameter 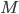 is important. One public key wouldn’t be enough as Bob couldn’t tell with certainty what the outcome of the swap test means. Bob has to test all
is important. One public key wouldn’t be enough as Bob couldn’t tell with certainty what the outcome of the swap test means. Bob has to test all 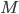 qubits. He needs at least
qubits. He needs at least 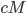 successful tests for some threshold
successful tests for some threshold  (it depends on his security level and the noisiness of the quantum channel, in an ideal channel it could be 1).
(it depends on his security level and the noisiness of the quantum channel, in an ideal channel it could be 1).
Quantum Public Key Distribution
I explained how Alice signs the message and how Bob validates it but in order for Bob to validate a message he first need to acquire the quantum public key. It is not enough that Alice sends it to him because Alice could be the one cheating. She might want to trick two recipients of her message, Bob and Charlie, to disagree on the validity of her signature. She could just send them different public keys. Therefore Bob and Charlie need a way to verify the public key they got.
The obvious way, that is often used in real life modern cybersecurity, is to have a third party that we assume can be trusted. The third party would receive Bob’s and Charlie’s public keys, perform swap tests and if they agree, send them to intended recipients. However this assumption requires secure quantum channels between the third party and all the recipients, so it’s infeasible. What can be done about it is the following: Alice needs to send two copies of a public key to both Bob and Charlie. Then they can swap test the copies they got, exchange one copy and swap test again. Two copies are required in case one of the recipients is dishonest - if Bob sent his only copy of public key he would have no way of knowing if the same public key was returned to him (by no-cloning theorem he couldn’t keep a copy). Even with two copies a dishonest recipient could cause distribution phase to abort but he could do nothing else.
Protocol Security
Forging
Let’s assume that there exists an adversary Eve, who wants to replace contents of a signed message. In the worst case Eve can collect all 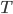 copies of each of the public keys. She can learn
copies of each of the public keys. She can learn 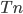 bits of information about each underlying private key but still has to guess the remaining
bits of information about each underlying private key but still has to guess the remaining 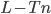 bits. Since
bits. Since  the probability that Eve would guess a key remains very low
the probability that Eve would guess a key remains very low 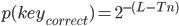 (probability to guess one bit in the key is ½ so to guess
(probability to guess one bit in the key is ½ so to guess 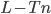 bits it is
bits it is 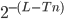 ). And Eve has to guess at least
). And Eve has to guess at least 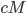 keys for the new message to pass the swap tests. This makes it extremely unlikely that Eve succeeds.
keys for the new message to pass the swap tests. This makes it extremely unlikely that Eve succeeds.
Non-repudiation
Alice might want to make two recipients - Charlie and Bob disagree on whether her message is valid or not. Mathematically this means that 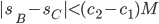 . That is, the number of swap tests that succeed for Bob is big enough, so he concludes that the signature is valid, while Charlie concludes otherwise (or vice-versa), because number of swap tests that succeeds for him falls below the minimum threshold. To do this, Alice could prepare a state with superpositions so that swap test would have equal probability of succeeding and failing. But then she still couldn’t control for whom the validation of her signature fails. Also, since
. That is, the number of swap tests that succeed for Bob is big enough, so he concludes that the signature is valid, while Charlie concludes otherwise (or vice-versa), because number of swap tests that succeeds for him falls below the minimum threshold. To do this, Alice could prepare a state with superpositions so that swap test would have equal probability of succeeding and failing. But then she still couldn’t control for whom the validation of her signature fails. Also, since 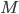 is large, it makes it extremely unlikely, that more than half of the states turn out to give one kind of result to Bob and another kind of result to Charlie.
is large, it makes it extremely unlikely, that more than half of the states turn out to give one kind of result to Bob and another kind of result to Charlie.
Conclusion
Quantum digital signature scheme seems to be more robust than the classical one, since it relies on physical property of the quantum world, that is, uncertainty principle. As of today, the classic digital signatures are still reasonably secure, and will remain secure until a large enough quantum computer is build. However, people and organizations who care deeply about their information security should consider using quantum cryptography methods in the near future to ensure the safety of their information and communications. That being said, it seems that there will alway be a trade-off in the quantum scheme, since quantum cryptography bears a large overhead, and the more security one requires, the bigger is the cost on performance.
Outro
Hopefully some of you found this read interesting or useful! It's been a bit of a pain in getting the math characters into this post and I apologize if some look bigger than others (there's a bug in Google Docs that messes up bra-kets when exporting to html).
Thanks for readin'!
Congratulations @crunchiness! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!