Sets of Julia part II
Hello to all, today I bring the second part on my study of sets of julia, in the previous post (https://steemit.com/science/@falcao12/sets-of-julia) only cover the part of the set of real numbers in this post will see what happens in the conjunct of complex numbers:

In figure 1 the green line represents the Julia set of the function:
F (x) = x^2 - 0.75
Let us now study the same function but in the complex plane, that is,
Where z is a complex number, that is, z = a + ib with a, b ∈ R and i =√-1
What happens when the value a0 is a complex number instead of a real number?
Let a0 = i have the following
a0 = i
a1 = f (i) = i^2 - 0.75 = -1.75
Note that a1 is a real number less than -1.5 therefore by analysis of previous post (https://steemit.com/science/@falcao12/sets-of-julia) {ak: k ∈ N} escapes to infinity .
If a0 = 0.5i then
a0 = 0.5i
a1 = f (0.5i) = (0.5i)^2 - 0.75 = -1
For this case a1 is a real number belonging to the closed interval [-1.5; 1,5], in consequence {ak: k ∈ N} converges.
In general if we take a0 = ci where c ∈ R then the condition that must satisfy c that {ak: k ∈ N} converges is as follows:
-1.5 ≤ (ci)^2 - 0.75 ≤ 1.5
−0,75 ≤ −c^2 ≤ 2,25
0 ≤ c^2 ≤ 0,75
−0,866 ≤ c ≤ 0,866
That is ci must be between -0.866i and 0.866i
In figure (2), the green part represents the julia sets of f (z) = z^2 -0.75, but only referring to the real axis and imaginary axis, that is to say we still have to study initial points of the form a0 = a + ib where a, b ∈ R - {0}
study of the initial points of the form a0 = a + ib where a, b ∈ R - {0}
If we take a0 =1/3 +5/9i we get the following iterations
a0 =1/3 +5/9i
a1 = f (1/3 +5/9i) = (1/3 +5/9i)^2 - 0.75 = -0.9475 + 0.3704i
a2 = f (-0.9475 + 0.3704i) = (-0.9475 + 0.3704i)^2 - 0.75 = 0.0106 + 0.3704i
a3 = f (0.0106 + 0.3704i) = (0.0106 + 0.3704i)^2 - 0.75 = -1.2424 + 0.0149i
a4 = f (-1.22424 + 0.0149i) = (-1.22424 + 0.0149i)^2 - 0.75 = 0.7933 - 0.0371i
a5 = f (0.7933 - 0.0371i) = (0.7933 - 0.0371i)^2 - 0.75 = -0.1221 + 0.5891i
In this case it is not clear what will happen as the number of iterations progresses, therefore it is time to carry out the calculations with a computer and a software, which in our case is MatLab
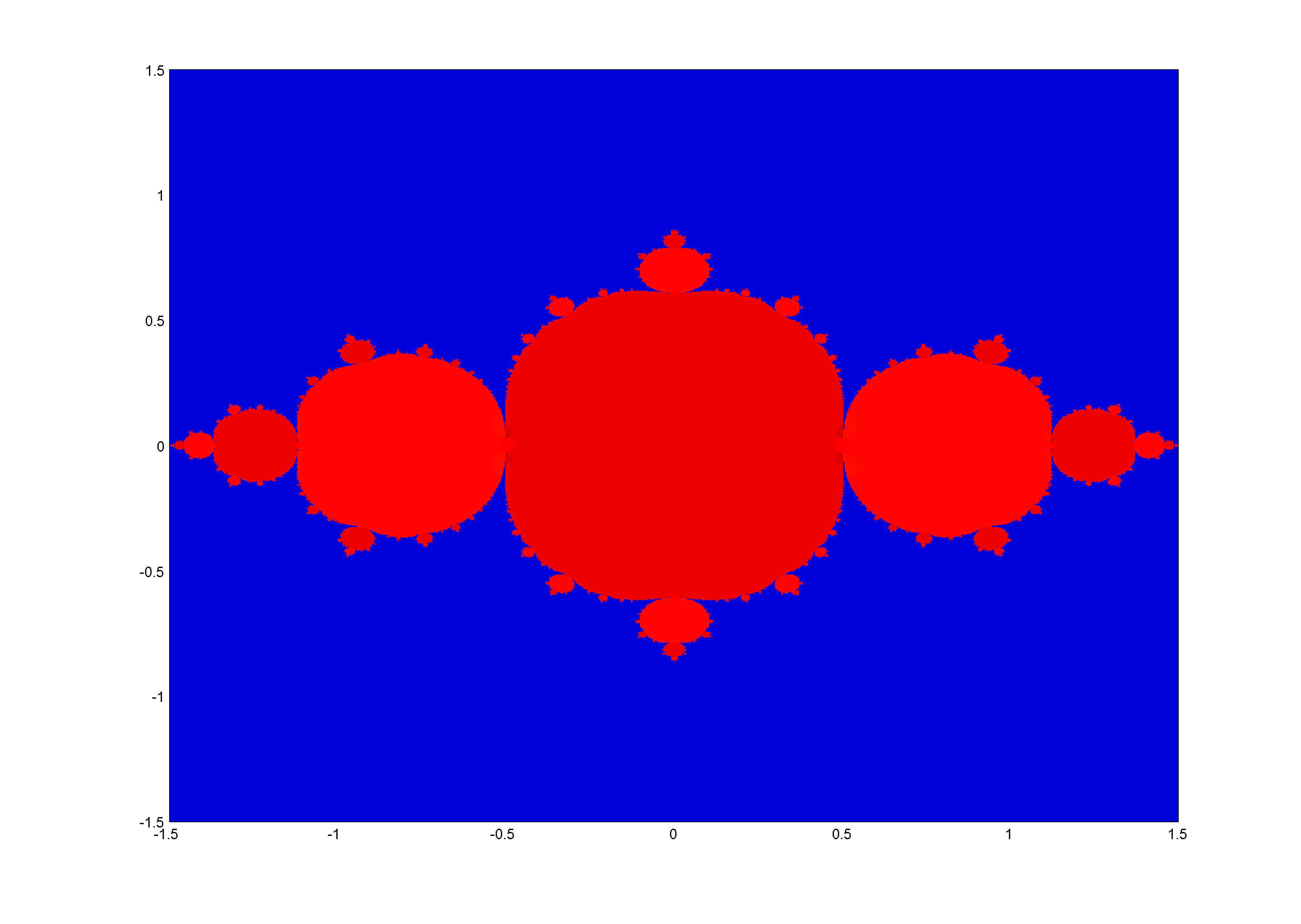
The figure (3), made in MatLab, we show the julia set of f (z) =z^2 - 0.75, where each starting point a0 = a + bi is taken in such a way that (a, b) ∈[-1.5; 1.5] × [-1.5; 1,5] and 400 iterations were done to study in behavior of {ak: k ∈ N}, the blue color indicates that the succession escapes to infinity, the Julia set in a reddish color is painted.
enjoy, resteem and follow me @falcao12
Resteemed your article. This article was resteemed because you are part of the New Steemians project. You can learn more about it here: https://steemit.com/introduceyourself/@gaman/new-steemians-project-launch