SLC21 Week1 - Learn more about variable types. Subroutines. Practice problems.
Assalamualaikum my fellows I hope you will be fine by the grace of Allah. Today I am going to participate in the steemit learning challenge season 21 week 1 by @sergeyk under the umbrella of steemit team. It is about variable types. Subroutines. Practice problems.. Let us start exploring this week's teaching course.

Come up with your own example similar to float f=7/2; that illustrates the loss (distortion) of value during division. Show how to fix it. Explain why this happens and how you fixed it.
Here is another example to explain the potential loss of value in the division due to integer division in programming. I have found another similar example which shows distortion during division this example is float result = 5 / 2;. In this example during the integer division the fractional part of the answer is discarded and it gives the answer of 2 except 2.5. So the result will hold the value of 2.0 when it will be converted to float. It causes the loss of accuracy.
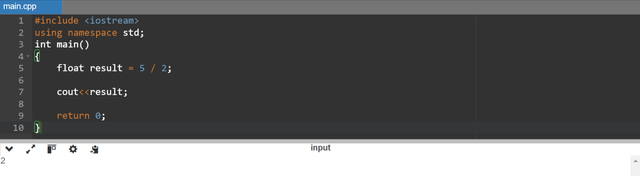
Solution
We can prevent this loss by setting one or both the operands to float or double. It will ensure floating point division.
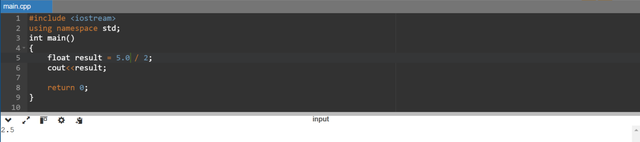
Here you can see that we are using 5.0 which is a floating point value and it is divided by 2. Now it will return 2.5 except 2. It preserves the fractional part in the answer as expected. When we explicitly make one operand float or double we inform the compiler to use floating point division and it keeps the fractional part in the result.
Why It Happens
This happens because in most of the programming languages when we divide two integers default to integer division it removes the decimal part and as a result it returns an integer. When we convert at least one operand to double or float before the division then it ensures floating point division and it preserves the decimal part.
Choose the type of data yourself and illustrate the limitation of its range: demonstrate the limit - from below (transition through the minimum value) and from above (transition through the maximum value. Also demonstrate the transition through the limit during the multiplication operation, explain the results.
Every data type has its own fixed upper limit and lower limit. I am using int data type to explain its upper limit and lower limit as well as the overflow of the value by multiplication.


Explanation
The complete explanation of the code is given below:
Overflow (Above Maximum Limit)
The variable
maxIntis intialized toINT_MAX. It is the maximum possible integer value. It denotes 2,147,483,647 for a 32-bit system.When we add
1to the variablemaxIntthen it overflows and the value is showed to the most negative value in theintrange and it gives the result of-2,147,483,648.
Underflow (Below Minimum Limit)
The variable
minIntis intialized toINT_MIN. It represents the minimum integer value which is-2,147,483,648.When we subtract
1from theminIntthen it underflows and wraps around the maximum positive value which is2,147,483,647.
Overflow Through Multiplication
The result of the expression
50000 * 50000is equal to2,500,000,000. And the result exceeds the maximum range of a 32 bit integer.the result is larger than the
INT_MAX. It wraps around and produces an incorrect overflowed value. The exact overflowed result depends upon the system and the compiler. But it will be a negative number which does not make sense.
This happens because the integer type has the fixed range. When an arithmetic operation exceeds this range it wraps around. This is known as overflow. Similarly when the value drops below the minimum value it is known as underflow.
find your analogue that 0.1!=0.1, that is, in some variable, there is a certain value, but the check shows that there is another number. Or 0.1+0.2!=0.3Why so?
In the floating point arithmetic the numbers such as 0.1 and 0.2 cannot be represented exactly due to the limitations in the binary storage. It leads to unexpected results such as 0.1 + 0.2 != 0.3. This behaviour is rooted in how computers represent the decimal fractions in the binary system.
Here is the example in C++ to explain this issue.
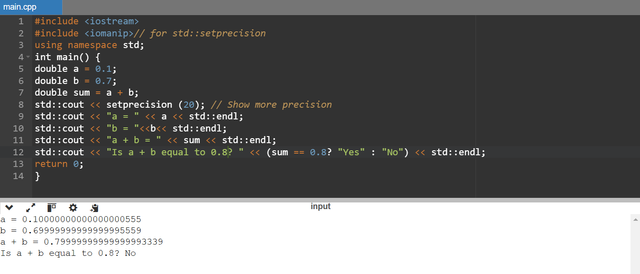
Explanation of the Code and Results
In this code:
We assign
0.1to variablea. Similarly0.7to variableb. Both are the float variables.We add
aandband the result is stored insum.Then we check if the answer of
sumis equal to0.8.
But the output of the program shows that the result is not equal to 0.8.
This happens because the floating point numbers follow the IEEE 754 standard. This standard represents them in the binary format. In the binary the fractions like 0.1 and 0.7 cannot be represented within the fixed precision of the floating point numbers.
They are stored in the approximate values. It leads to minor inaccuracies. So when we add 0.1 and 0.7 then the result is not exactly 0.8 but it is something like 0.79999999999999993339. And this result depends upon the limit of the precision.
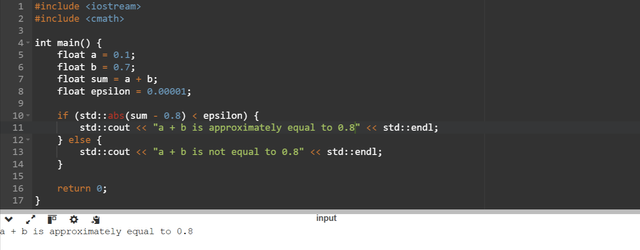
For the solution of this problem we should use small tolerance or epsilon to measure the small differences.
Here you can see that the epsilon is the small value it defines an acceptable range for the floating point comparisons. So instead of checking c == 0.8 we check the difference c - 0.8 to determine if it is smaller than the epsilon value. It returns the approximate value.
Based on the example of counting digits in a number, write a program that determines:
I have selected the task 3. In this task there is the need to count the occurrence of the specific digit in a given number. I will use while loop and it will continue as long as the n is greater than 0. I will create function and it will take n and digit as argument.
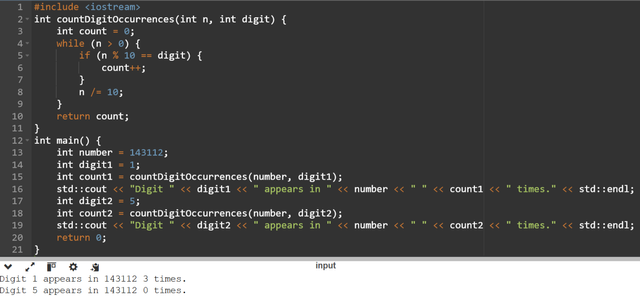
Here you can see the code the function is getting two arguments as n and digit. In each iteration we use
n%10to get the last digit ofn. For example ifn= 143112andn%10gives us the last digit which is 2.After that we check if the last digit is equal to the
digit. If we found the occurrence of the target digit we incrementcountby1.Then we remove the last digit by the integer division
n/10.It shifts the number to the right by one digit. For example if
n=143112thenn/10gives the output of 14311 by shifting last digit.Then we repeat the process again and again until
nis reduced to0it ensures that all the digits have been checked.Once the loop is completed then the
countholds the total number of occurrences ofdigitinn. At last the functions returnscount.
As preparation for the next lesson and to review the past, find the largest of two numbers, then the largest of three numbers (this is a different subtask), then the largest of four, five, six, seven - stop when you understand that you are not following a rational path and for larger quantities you should do it differently. Complete the task only using the conditional operator if().
I will complete all the sub tasks with the help of the if conditional operator. The conditional operator will find the largest number from the given numbers. Here is the C++ code to find the largest of two, three, four, five, six, and seven numbers using only if statements.
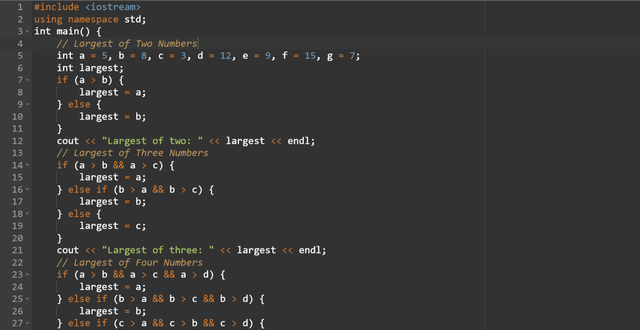
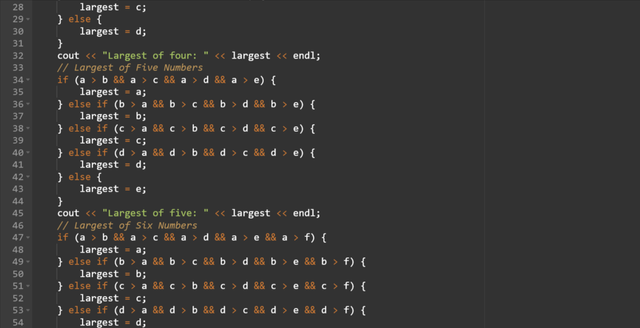
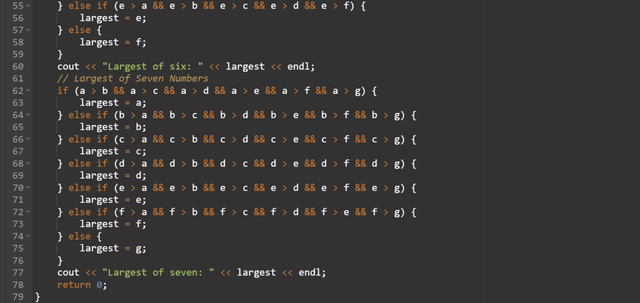
Here you can see that as the number of inputs increases the code becomes complex. Each section of the code finds the largest number from the two up to seven numbers. using only if conditional operator. This is a lengthy approach and it becomes impractical for the larger numbers.
Output

Here is the output of the program which is representing the largest number from the given numbers. I have defined all the numbers at the top. There is the use of the if and else statements. And it makes the code longer because we need to add more nested if conditions. This is not a scale able approach. If we use array or a loop then the code can become more simple and easy to understand.
Perform the previous task using the ternary operator.
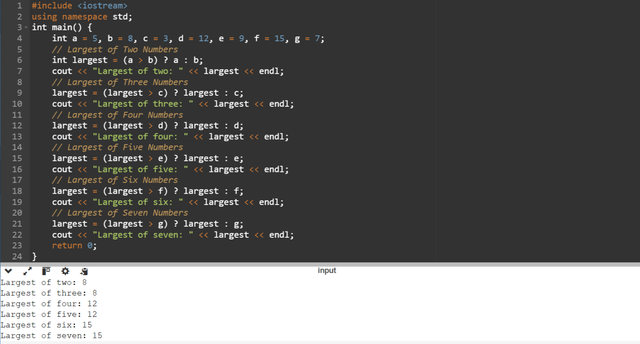
Here I have started by determining the largest value of the first two numbers
aandb.For the each next number I am using previously determined
largestvalue. Then I am comparing thelargestvalue with the next number. If thelargestis greater then it remains unchanged. But if thelargestis less then it takes the value of the new number.The program is printing the largest number after each comparison. This approach has reduced the redundancy in the code.
Perform the previous task by writing a function max() and using it.
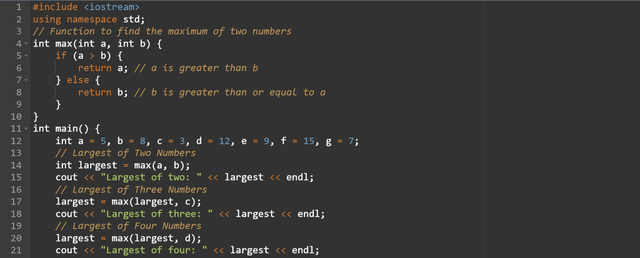
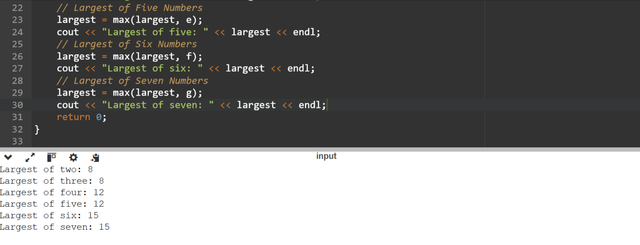
The
max(int a, int b)function takes two integer parameters. It returns the larger number by checking the numbers using theifstatement. At the start to define the logic exceptifwe can also useternary operators.If
ais greater thanbthen it returnsbotherwise it returnsb.In the
main()function I have initialized the integer variablesa,b,c,d,e,f, andg.I am finding the largest number by calling the
max()function again and again. And in order to find the largest number I have started withaandb. Then I am updating thelargestwith the each additional number.The program is printing the largest number after each comparison. The sue of the
ifstatement has made the chore logic straightforward and easy to follow.
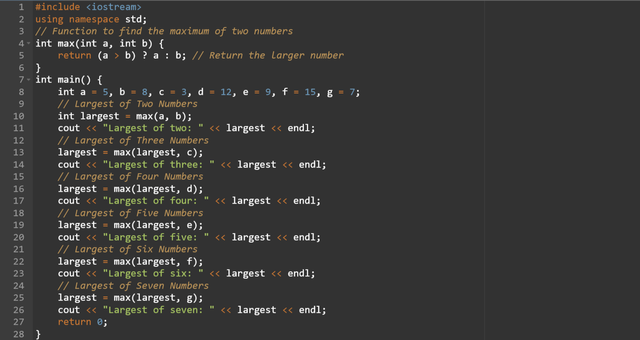

Here is the same working of the program using the function but with the ternary operators. It has removed some lines of code.
Write functions:
that will print all the divisors of a given number print_div(number) - you can skip printing one and the number itself. print_div(11) => (empty), print_div(12) => 2 3 4 6
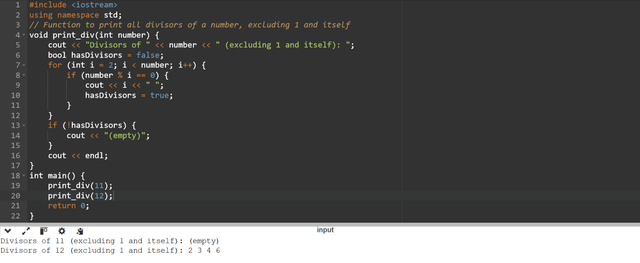
The
print_div(int number)will check the divisors for the number passed as a parameter. If it does not have any divisor excluding itself and 1 then it will returnempty. As an example in the above code we can see thatprint_div(11)has no any divisor except itself and 1 so the function is returning empty.On the other hand if the number passed to function has divisors except itself and 1 then it will print all the divisors.
print_div(12)will display2 3 4 5as these are the divisors of 12 excluding 1 and 12.
a function sum_div(number) that will calculate the sum of its divisors that are less than itself. sum_div(6) = 1+2+3=6, sum_div(10) = 1+2+5=8,
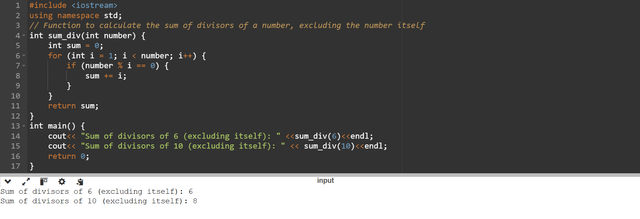
The function sum_div(int number) is accepting a number as a parameter and then it will use this number to calculate the divisors of that number by excluding itself which is controlled by the condition in the for loop. I have set that the iterations should be carried out until i is less than number.
sum_div(6)calculates the sum of divisors of 6 by excluding 6 itself. The divisors are 1, 2, and 3, and their sum is 6.sum_div(10)calculates the sum of divisors of 10 by excluding 10 itself. The divisors are 1, 2, and 5, and their sum is 8.
a function that will find and print perfect numbers from 1 to n (the number passed to the function). perfect numbers are those where the sum of divisors less than the number equals the number itself.
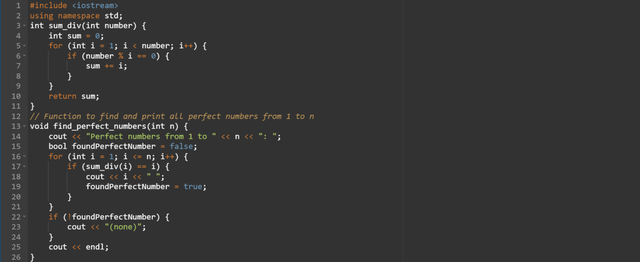
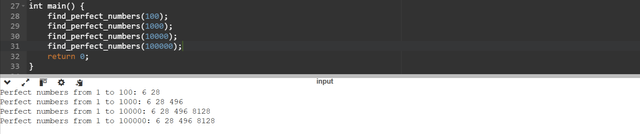
sum_div()function is used to calculate the sum of all the proper divisors of a given number by excluding the number itself. This function helps to determine if a number meets the definition of the perfect number or not.The
find_perfect_numbersfunction iterates through the numbers from 1 to n. It checks each number if it is a perfect perfect number by comparing it to the result ofsum_div(i).A perfect number is printed if the sum of its divisors is equal to the number itself.
I invite @alejos7ven, @suboohi, and @drhira to join this contest.
I have compiled all the code of the tasks in a famous online compiler which is OnlineGDB
https://x.com/Shaki70Akmal/status/1852420806267019560