SLC21 Week1 - Learn more about variable types, subroutines, practice problems

Hello everyone! I hope you will be good. Today I am here to participate in Steemit Learning Challenge of @sergeyk about the variable types, subroutines and practice problems. It is really an interesting and knowledgeable contest. There is a lot to explore. If you want to join then:

---

---

Join Here: SLC21 Week1 - Learn more about variable types. Subroutines. Practice problems.

---

---

Designed with ^Canva

Come up with your own example similar to float f=7/2; the one that illustrates the loss (distortion) of value when dividing. But show how to fix it. Explain why this happens and how you fixed it?

Sometimes we see distortion in the values specifically when we divide the numbers. Here is a similar example to float f=7/2. In this example I will show how value distortion happens during the division when we use integer data types.

float result = 9 / 4 this example is similar to the float f=7/2. The expected result of this example is 2.25. But while the calculations it will return 2.0.

Explanations

In the above example I am dividing two integers 9 and 4. Both the numbers are integer. C++ performs integer division and it drops the decimal. This is the reason it results 2 instead of 2.25. This result is assigned to the result variable and stores 2.0 rather than the expected result which is 2.25

Fix

This is not a nig problem to be fixed. We can simply fix this problem. We can cast one or both the operands to float or doube. It will ensure the division happens in floating point.

float result = (float)9 / 4 here the problem has fixed and by setting the operands to float now it will perform floating point division. Now it will return 2.25 as result.

---

Choose the type of data yourself and illustrate the limitation of its range: demonstrate the limit - from below (transition through the minimum value) and from above (transition through the maximum value. Also demonstrate the transition through the limit during the multiplication operation, explain the results.

In the lecture the professor explained different data types and their use cases and it was really informative for me to enhance my concepts more.

I will use short data type. I have chosen this data type because this was not explained in the lecture and it will add value and it will be a plus point for the readers to read a new data type with its limitations. short data type has the range of -32,768 to 32,767.

Here I have used C++ language to explain this data type short.

Explanation

Upper Limit Transition

• Here I have initialized max_val to maximum possible value for the data type short which is 32,767.

• As max_val is already at the last top value and if we further add 1 to max_val then it causes overflow. This overflow transitions the value to -32767 because of the binary wrap around.

• This has happened because short uses a fixed number of bits which are usually 16.

• So when we add value beyond the maximum limit it causes it to loop back to the minimum value.

Lower Limit Transitions

• I have initialized min_val to the possible minimum value for short which is -32,768.

• If we subtract 1 from the min_val the it causes underflow. This underflow transitions the value to 32,767 which is the maximum positive value for short.

Multiplication Overflow

• I have created a variable overflow_example. I have initialized it to 300.

• When I am multiplying it with 200 then the output or the multiplication result exceeds the maximum range of short. This causes to result an incorrect value to overflow.

• The correct result should be displayed as 60,000. But the value wraps around in the short range and it results a distorted value which is meaningless.

Why This Happens

In each case we can seen that the overflow or underflow is occurring. The reason of this overflow and underflow is the short data type has a limited range . Because of its limited range on its fixed number of bits which is 16 bits in most of the systems. So when the value exceeds the pre-defined range then the value of wrapped around due to the nature of the binary arithmetic.

In order to avoid overflow in the data type short we can change the data type to int or long which can store larger values.

---

---

Find your analogue that 0.1!=0.1, that is, in some variable, there is a certain value, but the check shows that there is another number. Or 0.1+0.2!=0.3Why so?

This phenomenon shows that how the floating point numbers are represented in the memory. It commonly occurs because many decimal fractions cannot be represented precisely in binary system. Here I have explained this issues and why it happens with the example using C++ language.

Explanation

Decimal to Binary Conversion

The decimal numbers such as 0.1 and 0.2 cannot be represented exactly in the binary system. Similarly 1/3 cannot be represented precisely in the decimal form. It becomes an infinite decimal value which repeats itself such as 0.333.... When we store 0.1 and 0.2 as double then these values are stored as very close approximations. But they do not presents the exact values.

Precision Errors in Addition

When we add 0.1 and 0.2 together the imprecise binary representations lead to a result that is very close to 0.3 but it is not exactly same as 0.3. The computer represents a+b as 0.30000000000000004 which is not exactly equal to 0.3. This is the reason that the equality check a + b == 0.3 becomes fail and similarly 0.1 + 0.2 != 0.3

Why This Happens

Floating point numbers in computers are represented based on the IEEE 754 standard. It stores the numbers in the binary form with fixed number of bits. Because many decimal numbers do not have exact binary equivalents. They are approximated within the limits of the floating point format. These minor differences are accumulated in the operations such as additions. It leads to precision error.

---

---

Based on the example of counting the digits of a number, write a program that determines

I will write the program by solving all the tasks in C++ language.

Explanation

I have created 3 different functions to perform the calculations of the respective tasks. Here is the explanation of the functions:

sum_of_digits

• This function sum_of_digits(int n) is taking an integer n. It is extracting each digit by taking n % 10. Then it is adding the digits to sum. It divides n by 10 to remove the last digit. It repeats itself until n is 0.

repeated_sum_of_digits

• This function calls sum_of_digits again and again until the result is a single digit number. It gets the same result by again and again summing the digits of the intermediate sums.

count_digit_occurrences

• This function is extracting each digit from n using n%10 and then it is incrementing the count if the extracted digit matches the digit parameter. It removes the last digit by dividing n by 10. It repeats the functionality until n is 0.

This is the output of all the tasks from 1 to 3. The output of the first task is 18. The result of the second task is 9 and similarly the last task has the output of 3 and 0.

---

---

As a preparation for the next lesson and repeating the previous one, find the largest of two numbers, then the largest of three numbers (this is another subtask), then the largest of four, five, six, seven - stop at that as soon as you understand that you are not following a rational path and for a larger quantity it should be done differently. The task can only be performed using a conditional operatorif()

I will perform this subtask by using conditional if operator in C++ language. For the more clarity I will write separate functions for different cases and in those functions I will use conditional operator if. I will also highlight the inefficiency of this approach as the number of inputs increases.

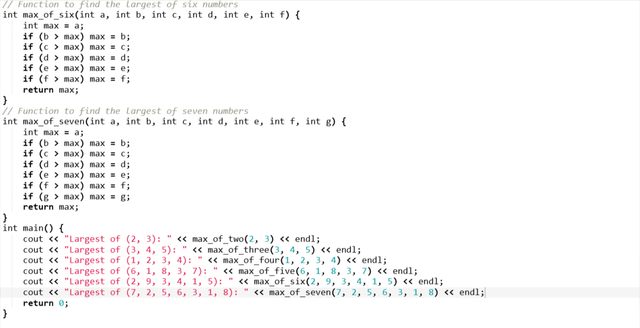
Here you can see in order to make the code more clear I have created a separate function for each check condition based on the number of digits. Each function finds the maximum of the specific number of inputs by comparing the each number. It updates the value of the variable max. This approach is working to find the largest number from the given numbers but as the number of parameter increases this approach becomes inefficient. For the larger inputs this approach requires a unique function for each specific count of numbers.

This is the output where we can see the largest number from the different available numbers. This task becomes impractical when we find the maximum of larger sets of numbers such as 10 or 15 or higher.

---

---

Perform the previous task through the ternary operator.

We can solve the previous task with the help of the ternary operators ? :. I will write each function to use ternary operator instead of if statements.

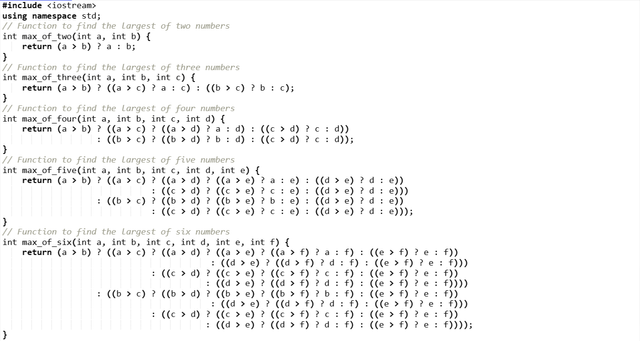
Here is the complete code using the ternary operators. Each function is suing the ternary operator to select the maximum value. There are nesting conditions by following the pattern (a > b) ? a : b. But as I moved to the larger number of variables it became very complex and it was becoming very hard for me to handle it.

You can see that the ternary operators have given the same output of the previous task because of same logic and working. So we can use ternary operators as the place of the conditional if. This approach works but it becomes very difficult to manage the larger set of numbers. Because the nesting structure becomes very complex.

Complete the previous task by writing the max() function and using it.

I will define a general purpose max() function. It will take an array of integers and its size as input. Then the function will find and return the largest element in the array. The use of the function to perform the calculation will surely make the code simple.

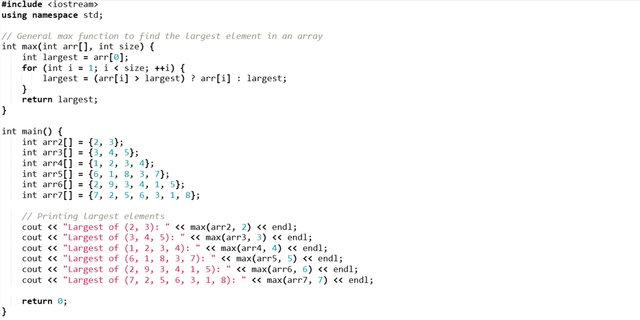
Explanation

The max() function is working as follows:

• I have set the largest variable to the first element in the array.

• Then the condition is checking each element in the array if it is greater than largest. And if it is greater then it is updating largest by storing the new value.

After checking all the elements through the loop the largest will return return the maximum value from the array. I have used arrays to make the code more easy for me and to make it simple and short.

The max() function simplifies the code than the previous both the methods. There is no need to write the separate functions or the complex ternary operators. This is an efficient approach.

---

---

Write the functions

which will output all the divisors of the specified number print_div(number)- one and the number number itself can not be output
print_div(11) => (empty), print_div(12) = > 2 3 4 6

In order to write the print_div function which will output all the divisors of given number and it will exclude 1 and the number itself. I will iterate from 2 to number/2to check for the divisors. Here is the complete program with function in C++:

Explanation

• print_div(int number): This function will iterate from 2 to number/2 to check if each number is a divisor such as number % i == 0 and if i is a divisor it will print i.

• Edge Case Handling: If there is no any divisor found like a prime number such as 11 then the program will output "empty". It will indicate the lack of divisors between 1 and the number itself.

In the output we can see the expected output. The solution efficiently finds and prints all divisors between 1 and the specified number. It is excluding 1 and the number itself.

a function sum_div(number) that will calculate the sum of its divisors that are less than itself
sum_div(6) = 1+2+3=6, sum_div(10) = 1+2+5=8,

Here is the function sum_div in C++. It will calculate the sum of the divisors which are smaller than the specified number.

Explanation

• sum_div(int number): This function will iterate from 1 to number/2 and it will check eaxh numberto see if it divides number with no remainder.

• During the execution of the program if the divisor is found then it is added to sum and the value of the sum is updated.

• Then at the end the function returns the total sum of the divisors less than the number.

The function has calculated the sum of the divisors efficiently for the given examples.

a function that will find and print perfect numbers from 1 to n (the number passed to the function)
perfect numbers are those where the sum of divisors less than the number equals the number itself.

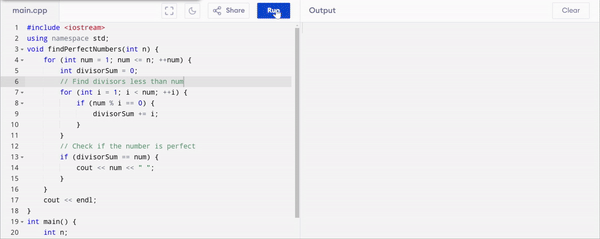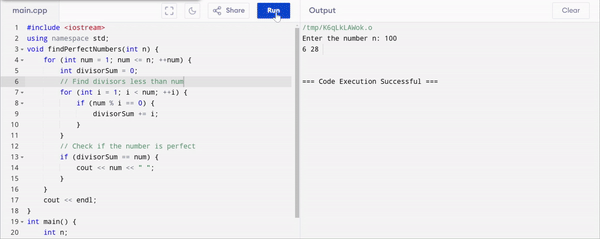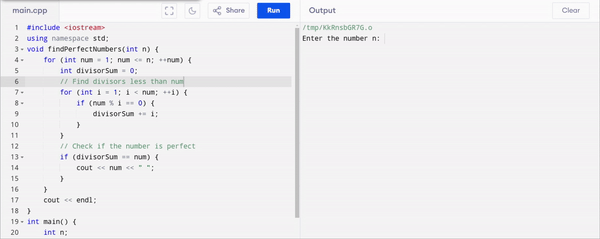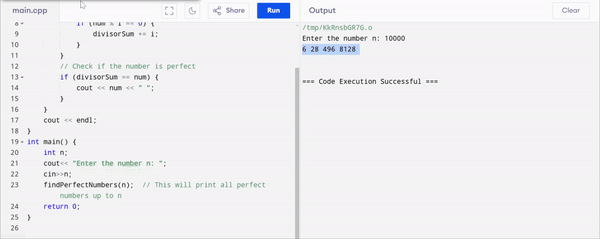
• Here is the complete code of the function and program in C++ to find and print the perfect numbers from 1 to n. I have set that the user will entern` and according to that value the program will be executed.

• I have used void findPerfectNumbers(int n) to find perfect numbers up to n.

• The divisorSum accumulates the sum of divisors for each num.

• If divisorSum is equal to num then the number is printed as a perfect number.

You can see in the output I have used different values for n and each time the program is calculating the perfect numbers from 1 to the entered number by the user.

---

---

I invite @enamul17, @mostafajaman, @fombae to join this programming course.

---

---

Disclaimer: I have used OneCompiler and Programiz to execute the code and to get the output.