SLC21 Week4 - Recursia
Hello everyone, welcome to my lastest homework for @sergeyk 's recursia course SLC21 Week4 - Recursia
This time on a complete rush as this was prepared Sunday hours before the deadline, let's get started.

Thumbnail from Pixabay

Recursion is a concept in programming where a function is able to call itself in it's current function or by another one, by dividing the big problem into smaller ones. Imagine it like a loop where you have code that keeps running inside it but in this case it's a whole function that runs as long as the condition is met.
A FRACTAL is that type of pattern that no matter how much you zoom in or out. It is related to recursion because this concept of programming is used to generate fractals. Imagine it like a never ending pattern or an infinite one, the repeating process over and over again in generating the pattern will end in a fractal.
Here is a cool fractal example https://www.youtube.com/shorts/XbDusuz9wfU

Now to find the largest value we could simply google them and create a table, but we want to show them via code, at least for a couple of the data types.
Let's start with INT.
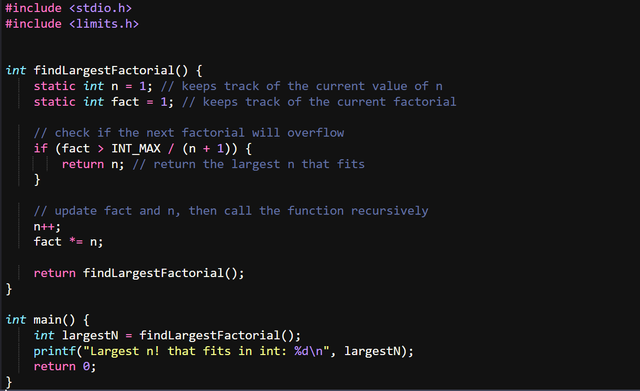
The idea behind this recursive code is to declare a variable that holds current value of n and current value of the factorial fact and with the use of the limits library we can use the MAX value of a data type in our code.
As long as fact is lower than our INT_MAX/(n+1) we increase the n and do another multiply. We use INT_MAX/(n+1) because this is the overflow check, INT_MAX/n is the cap size of our int, INT_MAX/(n+1) is the next value which overflows our int limit.
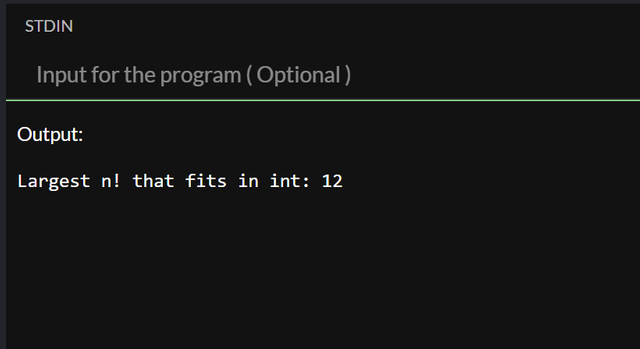
While running the code above we get this result, Largest n! that fits in int: 12
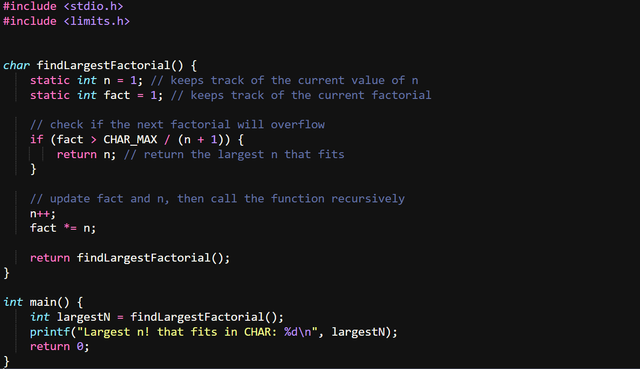
Now let's check CHAR, the code is similar, with just a simple change we get the CHAR limit.
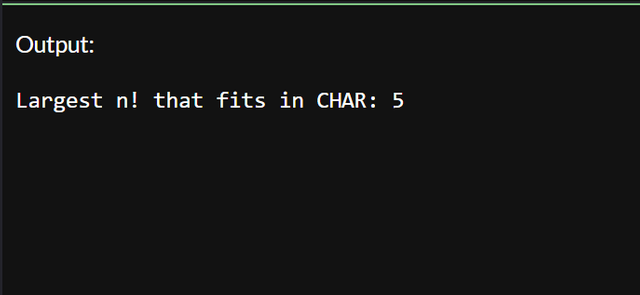
With the following output:
INT_MAX was replaced by CHAR_MAX to get the results for our second data type.
How would the factorial multiplier look like because I don't know why I haven't used them both in the code above:
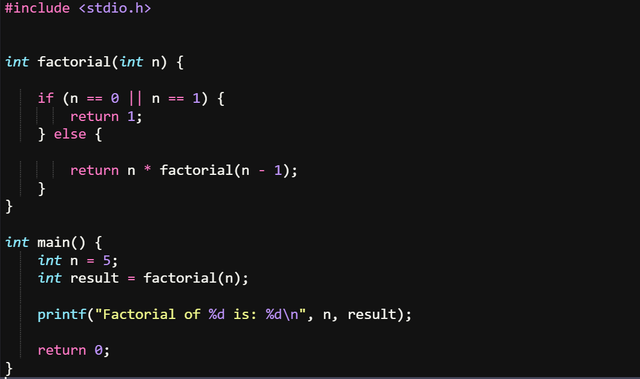
And the output:
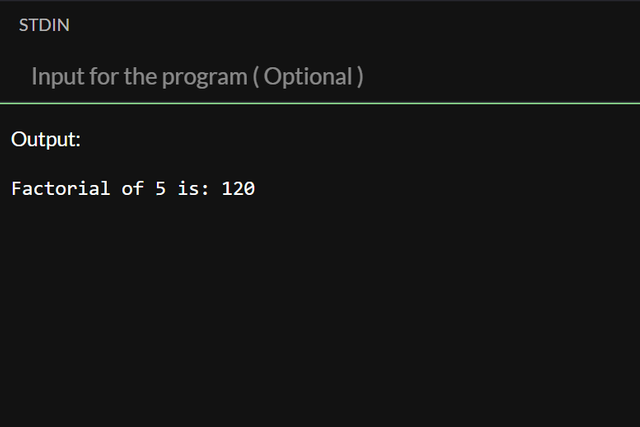
Using this we can reach the largest N for all data types, even though Factorial is not worth being used with all the data types I will still list down all of them.
| Data Type | Largest N | Factorial of N (N!) |
|---|---|---|
signed char | 5 | 120 |
unsigned char | 5 | 120 |
int | 12 | 479,001,600 |
unsigned int | 12 | 479,001,600 |
long | 20 | 2,432,902,008,176,640,000 |
unsigned long | 20 | 2,432,902,008,176,640,000 |
long long | 20 | 2,432,902,008,176,640,000 |
unsigned long long | 20 | 2,432,902,008,176,640,000 |
float | 34 | 295,232,799,039,604,140,847,618,609,643,520,000,000,000,000,000 |
double | 170 | 7.257413248004443e+306 |
long double | 1754 | Too large to compute in typical systems |

The limit being reached before terminating varies based on multiple factors, with some research we have the following things that can change the number of calls counted before terminating a recursive call.
- System Stack Size - this limits how deep recursion can go, having a too low limit will throw an overflow error and terminate earlier
- Compiler Settings - depending on the compiler, some might be more optimized towards recursion
- Operating System/Platform - OS settings can determine the default stack size
These number of recursive calls can be modified in a few ways:
- Increasing the Stack Size Limit
- Tail Call Optimization, which optimizes recursive calls
- Recursion Depth Control, adding an artificial limit for recursion depth calling, an example could be limiting the calls based on a variable directly in your code.
On a short description the main ways to increase/decrease the number of recursion calls are, changing the stack size, modifying compiler settings and changing your recursion logic.

Let's see for the factorial code mentioned on the previous task how many calls did it make for N = 5.
The calls are like this
factorial(5), this one calls factorial(4), we move to the next call
factorial(4), this one calls factorial(3), we move to the next call
factorial(3), this one calls factorial(2), we move to the next call
factorial(2), this one calls factorial(1), we move to the next call
factorial(1), this one gets to the base case and returns 1
So in the end we have 5 calls here plus the one where the first factorial is called, this gets us to 6 times (5 recursive + 1 original).

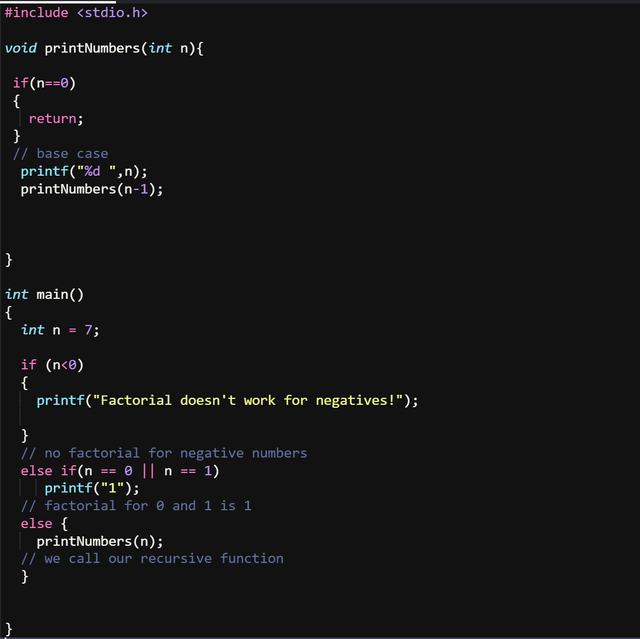
Printing the numbers from 1 to n shouldn't be that difficult, imagine a for loop from 1 to n that prints each loop the number, we are going to change that in a recursive function where each call of the function we check if our value is between 0 and n, if true we call the function with n-1 and print the value. Once our function will reach 1 it will trace back to our n value and print each value. The code should be something like this:
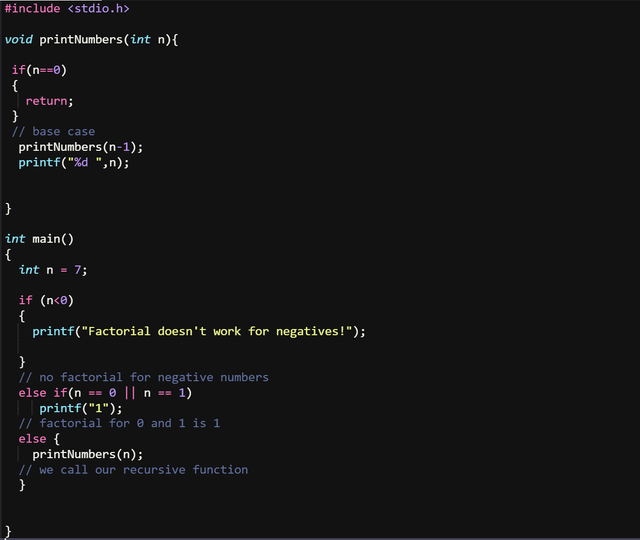
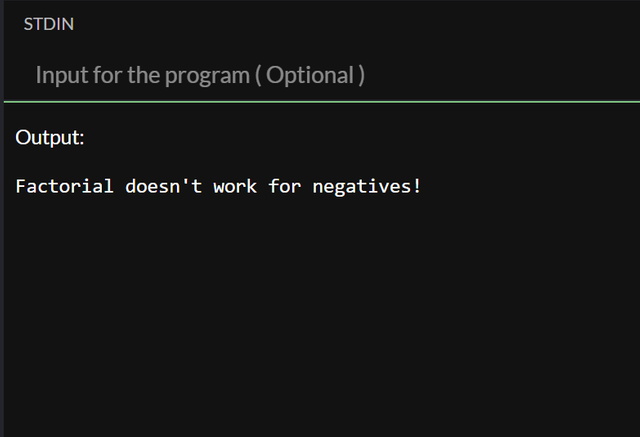
Right after creating the function I remembered that factorial for negative numbers is not possible, and for 0 and 1, it is 1, we'll avoid this in our code anyway, so I placed a quick check for these..
The output for n=7 looks like this:
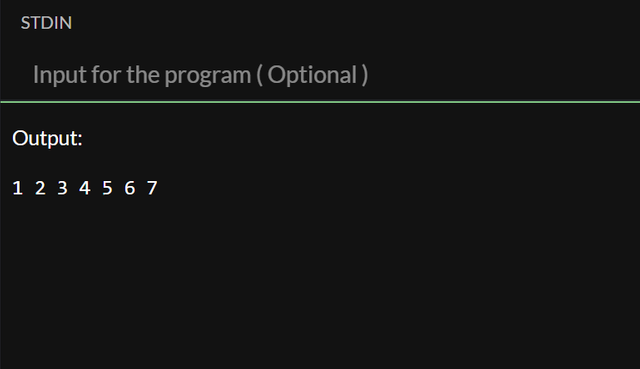
While a negative number or 0 would return this:

Now the other way around. You might ask yourself why would @sergeyk ask you two work on two similar tasks, let's solve the task and get some conclusions after, I'll have to check first.
After investigating what needs to be changed from the task above, it's actually pretty simple, we just have to swap two lines, like this:
Output:
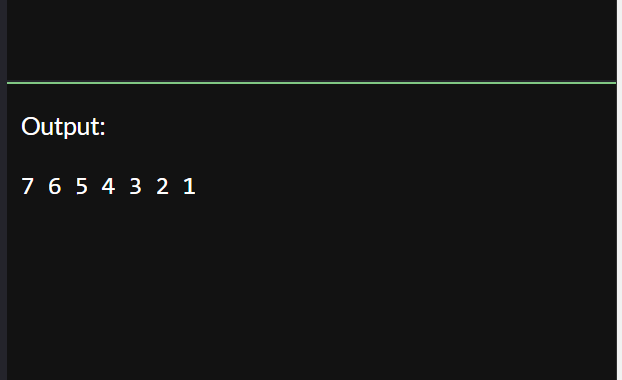
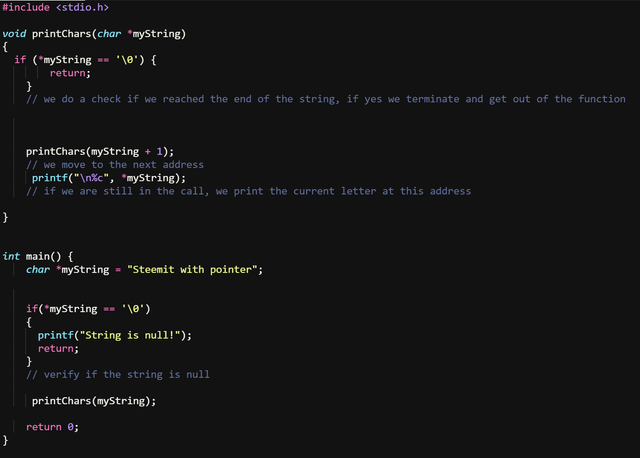
The function call and the printf were swapped, changing this order changes the way the recursive function calls itself and prints.
That's why @sergeyk came with these two tasks, for the user to understand how the call stack would work in these two cases, how the structure of recursive calls would print the value, such a small detail would create so different outputs.
- for 1 to N, the printing takes place after the recursive call, the stack will go from the smallest value upwards
- for N to 1 the printing takes place before the recursive call, the stack will go from the largest value downwards
This was more about how the Stack grows and shrinks and not about some simple printing of numbers.

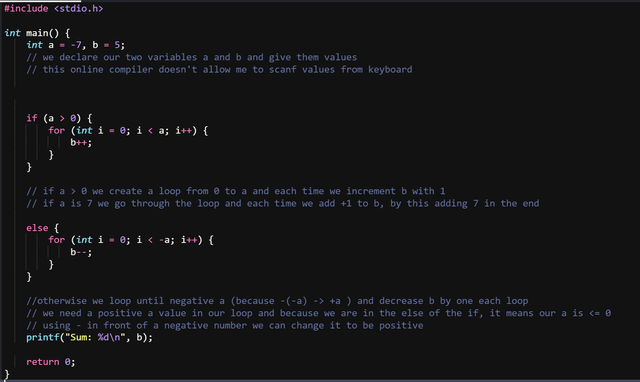
Let's do it with a loop first, we need to use to loops inside an if / else statement like this:
This is the output:
The idea behind this approach is pretty simple, you pick one of the two values, and you create a loop from 0 to that value where each time to increment the other value by one.
It's like each loop you make, you add +1 to the other value, and because the number of loops equals the value of your other number you add +1 that amount of times.
In this example above I loop through the first FOR the amount of times represented by a, and each time b gets a +1 value. Going through it 7 times, means I add +1 for the 7 loops I do and it's the same result as adding them directly.
Now the thing changes when there's a negative value, in this case we need to substract 1 and make sure we have a positive value in our loop, that's why in my example I added -a in the loop. -(-a) -> +a, like -7 goes to -(-7) and it becomes positive +7.
Another thing that could be added is a check for the numbers if any of them is 0, but using for loop will will make it work even with 0 as value.
Now how can this be approached with recursion.
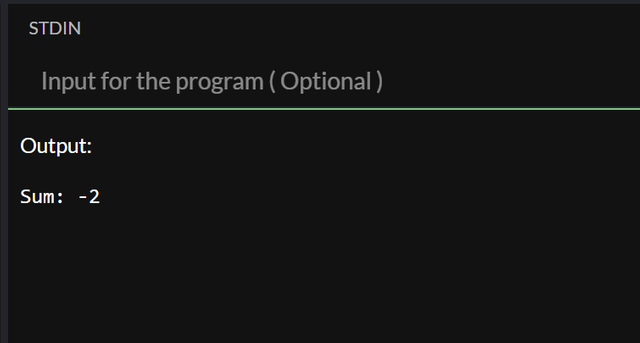
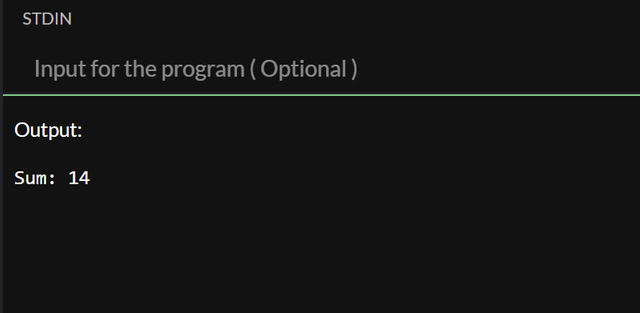
The output as it follows:
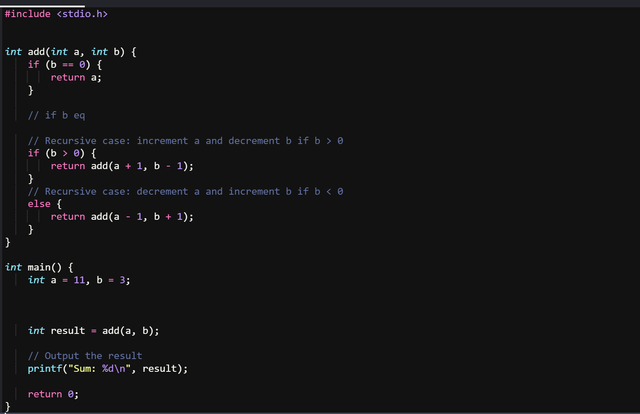
With a recursive function the sum gets added much faster because we increment one value and decrement the other. We increment and decrement values until the one chosen by us (this case b) gets to 0, when it gets to 0 it means we did enough incrementation to the other to reach the sum of the 2 numbers.
This is more like a conversion from the 2 loops to recursive function.

Let's start simple and progress each time more.
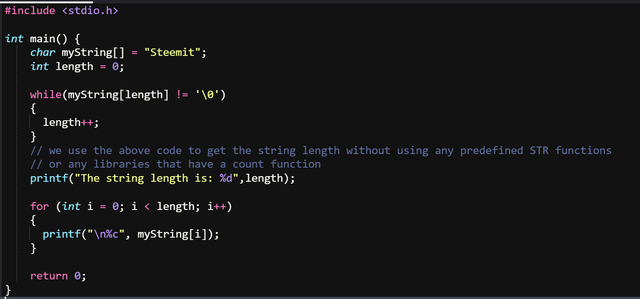
The above picture shows a simple print of a string letter by letter using an array, we simply find the string length and loop through it to print it letter by letter, this is the output.
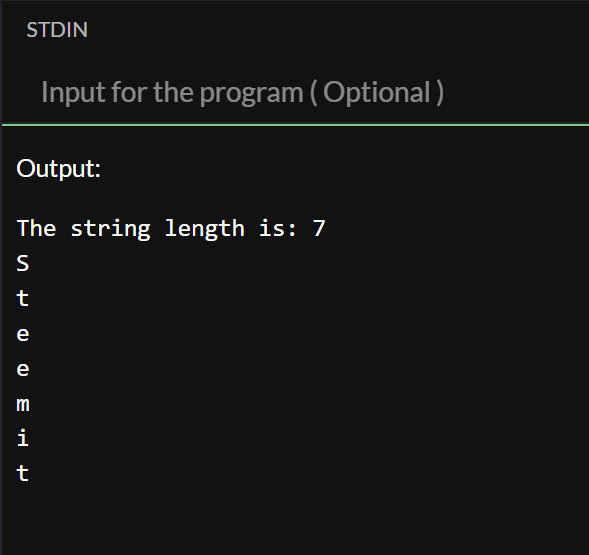
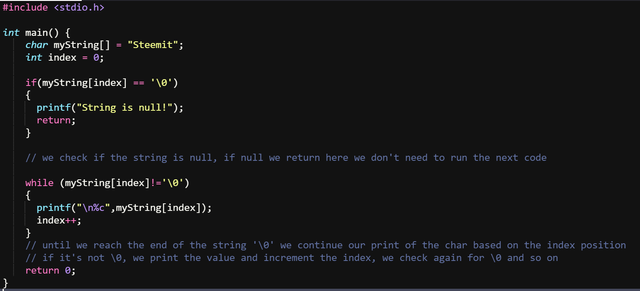
Now let's assume we don't know the length.
With the output:
In this case we don't know the length of the array, now we loop using a while until we reach \0, if we didn't find it we increment the index and continue our search. Once we reach the \0 our print would end as we reached the string end.
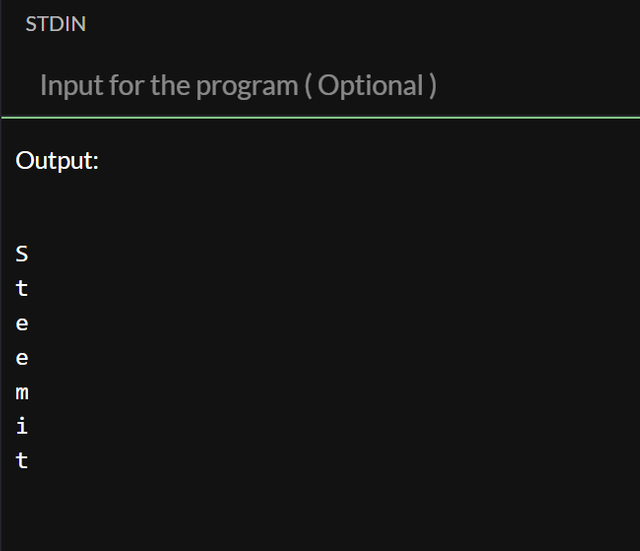
Let's see this example with pointers, where we point to the first position of the string and move from there.
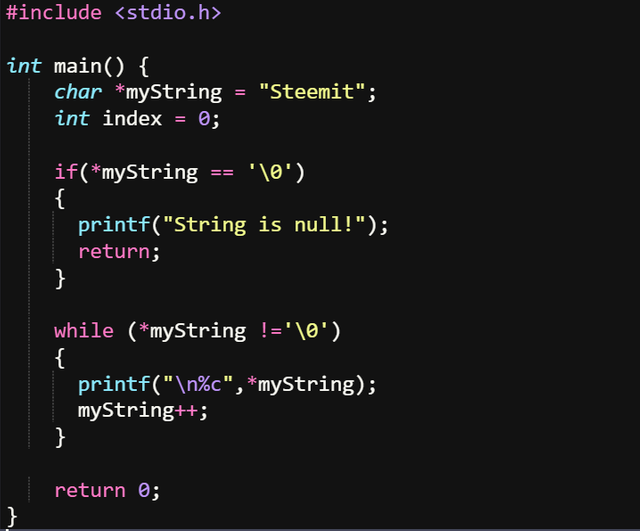
We start from the address of the first character in the string and increment it until we reach \0. When we add +1 we move to the second address in the string, print it and move on, as long as we didn't reach \0 we'll continue this.
P.S: Now I see I forgot to delete the index declaration from the picture, that one isn't needed anymore
This is the output for the code above:
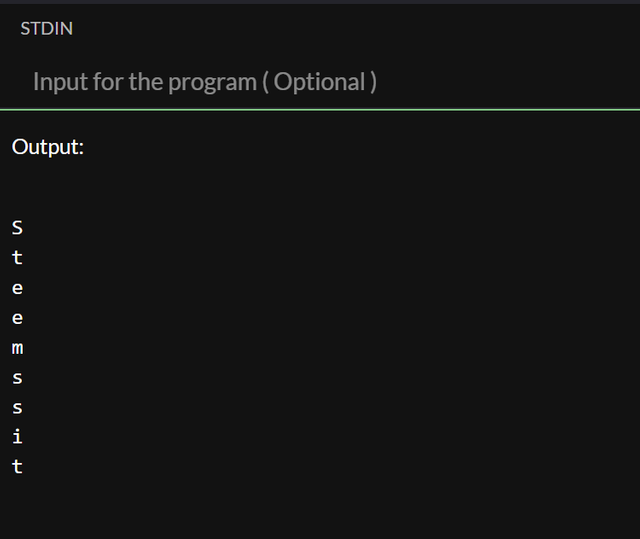
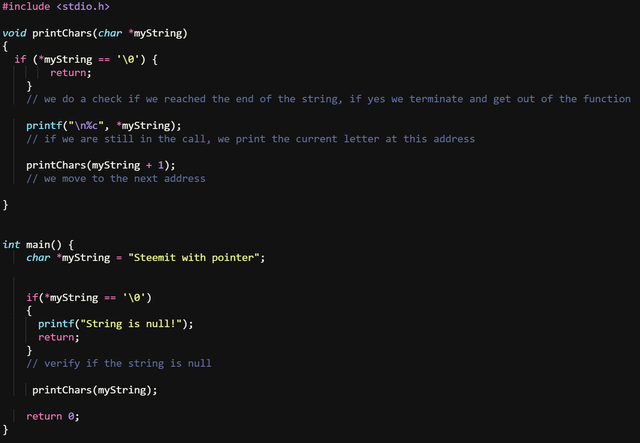
Now how do we adapt it to a recursive function:
With the output:
We are doing it as we did in the previous code using the pointer and moving from one address to the other, but this time after we print the current value we call the same function again but with the current address +1 to get the value of the next char in string. Once we reach \0 the return will terminate the function.

Now we know from the previous tasks that this can easily be achieved by swamping a couple of lines, we saw how to reverse print something in the two tasks we had above. The one to print values from 1 to N and N to 1.
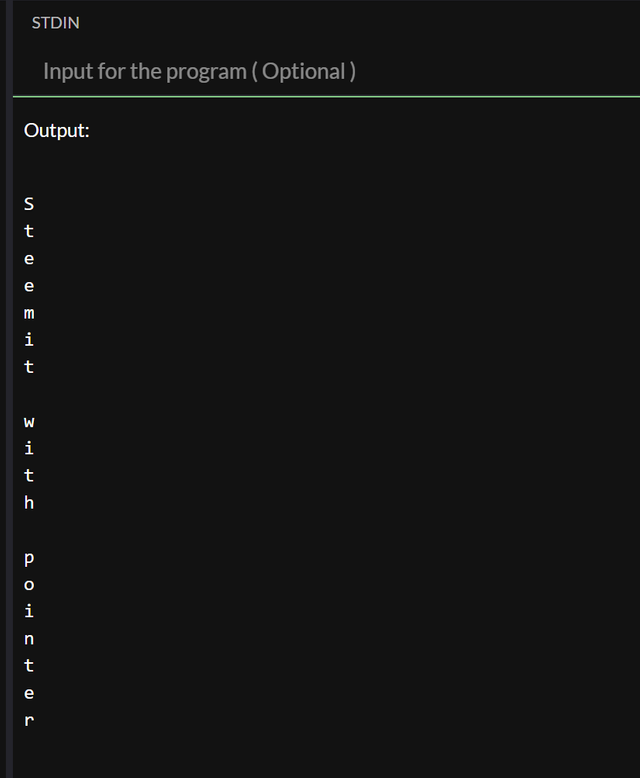
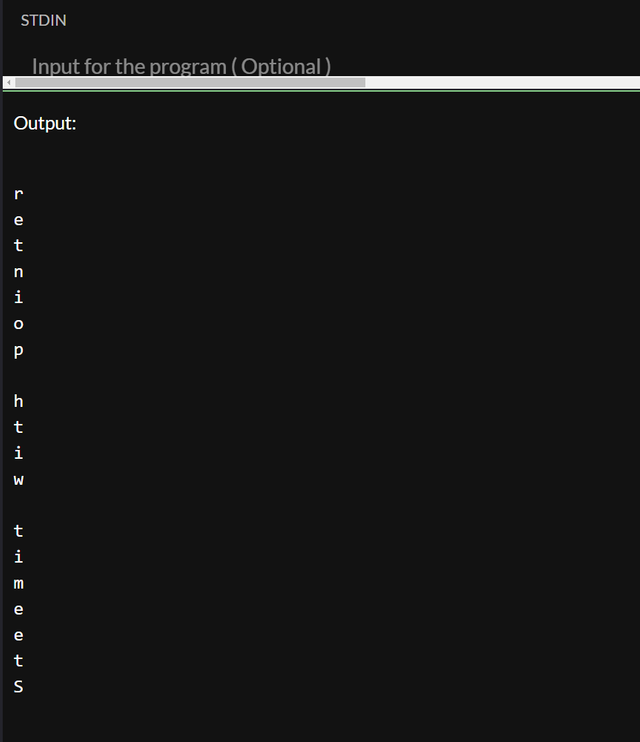
So our new code should look like this, I will keep the print of each char on a new line to show how we move from one to another:
With it's output:
That was it for this homework, in the end I'd like to invite @Mojociocio @r0ssi and @titans.
Thank you again @sergeyk for the amazing work and effort put into this course.