SLC21 Week4 - Recursion
Hello everyone! I hope you will be good. Today I am here to participate in Steemit Learning Challenge of @sergeyk about the Recursion. It is really an interesting and knowledgeable contest. There is a lot to explore. If you want to join then:
-min.png)
Describe recursion as you understand it. Have you encountered recursion before? How is the word "fractal" related to recursion?
What is Recursion?
Recursion is a technique in the programming where a function calls itself to solve the smaller parts of the same problem. It continuously do it until it reaches a base case. In the base case the problem can be solved without further recursion. This is an important technique and useful in the programming especially where we need to perform one action again and again.
For example, the factorial function:
int factorial(int n) {
if (n == 0) return 1; // Base case
return n * factorial(n - 1); // Recursive call
}
Here you can see the function which is calculating factorial of the number is a recursive function. The condition if (n == 0) return 1; makes it sure that the recursion stops when n reaches 0. The function calls itself with factorial(n - 1) and multiplies the result by n. This creates a chain of recursive calls until the base case is reached.
Have I Encountered Recursion Before?
We can encounter recursion in different problems such as:
- Calculating factorials.
- Generating Fibonacci sequences.
- Traversing trees or graphs
- Solving puzzles like the Tower of Hanoi.
If I talk about my experience about the recursion in the programming problems then I have encountered it in Factorials and Fibonacci Sequences programs. I used the recursive function while completing homework task in the steemit engagement challenge season 19 and week 6. There was the task to create a fibonacci sequence. I completed it in Javascript code. Moreover in the factorial example I have made many programs in C++ from the beginning of my journey in the programming.
How is "Fractal" Related to Recursion?
A fractal is actually a geometric shape. It can be split into parts. Each part is smaller and self similar copy of the whole. This concept reflects recursion. Because in the recursion the problem is reduced into smaller and similar problems.
For example Sierpinski Triangle is a fractal generated triangle. In the formation of this triangle recursive function is used by subdividing a triangle into smaller triangles. The self similarity in the fractals directly links to the repetitive structure seen in the recursion.

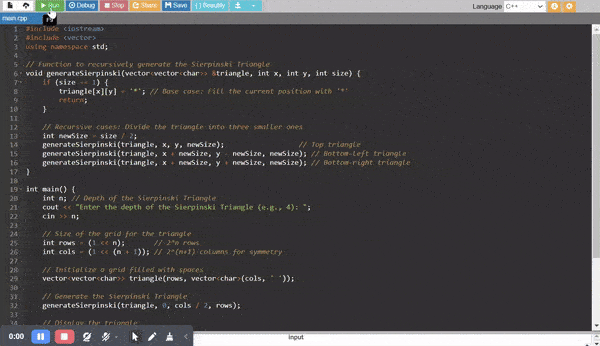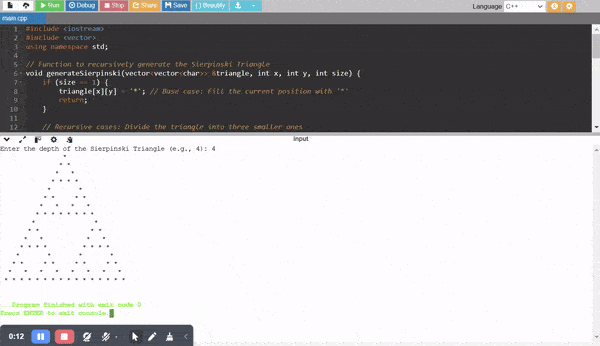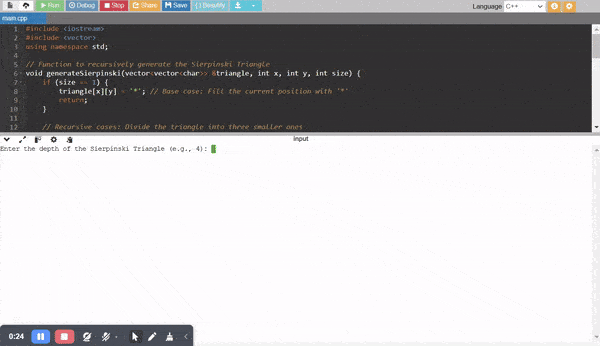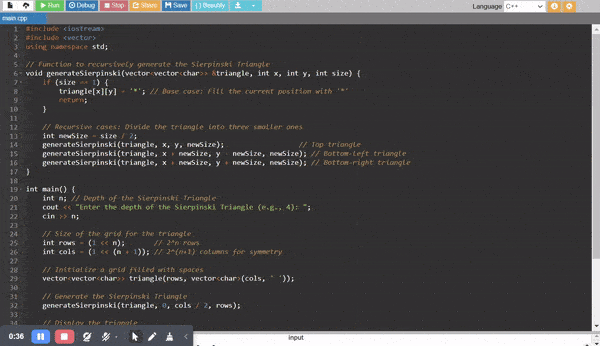
In the programming languages the generation of the fractals often involve recursive algorithms.
Explore the limit of what is the largest value of the factorial that can be calculated with a certain type of data.
The largest value of the factorial which we can calculate for a certain data type purely depends upon the data type. Because each data type has different size limit and when we exceed that limit then the values overflow and we cannot get the correct answer. Factorial grows rapidly so we calculate until the factorial exceeds the maximum value of the data type.
The largest factorial that can be calculated depends on the storage size, signed/unsigned range, and precision of the data type. Here is the summary for all the data types with respect to their maximum limit of factorial:
| Data Type | Bits | Max Value | Largest Factorial (n!) | Dependency |
|---|---|---|---|---|
char | 8 | 127 (signed) / 255 (unsigned) | 5! = 120 | Limited by small size (1 byte). |
short | 16 | 32,767 / 65,535 | 7! = 5,040 | 16 bits extend range modestly. |
int | 32 | 2,147,483,647 | 12! = 479,001,600 | Significant increase in range. |
long | 32 or 64 | ~2 billion / ~9 quintillion | 20! = 2.43e18 | Larger sizes handle up to 20!. |
long long | 64 | ~9 quintillion | 20! = 2.43e18 | No improvement beyond 64 bits. |
float | 32 | ~3.4e38 | 34! ≈ 2.95e38 | Exponential growth; precision loss. |
double | 64 | ~1.8e308 | 170! ≈ 7.26e306 | Precision enables much larger n. |
long double | 80-128 | ~1.1e4932 | 1754! ≈ 1.18e4932 | Most powerful for large factorials. |
The largest factorial computable depends on:
Storage Size: Larger types store bigger numbers.
Signed vs. Unsigned: Unsigned types nearly double the positive range.
Precision: Integer types compute exact values. The floating point types handle larger ranges but lose precision.
Overflow: Factorial grows super-exponentially, quickly exceeding small types.
Integer Types: The factorial values grow too fast to fit in the small data types and cause overflow. For example
charoverflows after5! = 120and similarlyshortoverflows after7! = 5,040. Similarly other data types also overflow after a specific limit which is fixed.Floating Point Types: These types can store very large values but these lose precision as the number grow. For example
floatsupports up to~2.95e38and it allows34!.Base Case and Overflow Detection: The algorithm stops when the factorial exceeds the limit of the data type.
Platform and Compiler Influence: The maximum value of the
longandlong doublecan vary by the system and compiler. So the maximum value of the data types is affected by the compiler and the hardware.
So these are the factors on which the largest computable value of the factorial depends upon. Each data type has a specific maximum value and we can only calculate the factorial value until the maximum value of the data type because when the value exceeds it gives garbage values.
Investigate how many calls the function will make before terminating. more details about this task are described in the lecture.
In order to investigate how many recursive calls a function makes before reaching its base and stopping I will consider the recursive structure and the base case logic. This is different from investigating termination due to stack overflow. Here the function terminates naturally when the base condition is satisfied.
Steps to Investigate Recursive Calls
1.Implementation of a Recursive Function with a Counter
In order to count each call I will use a counter variable to track the number of calls made during the function's lifecycle. We can pass it as a parameter by reference or we can use it as a global variable.

2.Testing for Different Inputs
The number of calls of a recursive function corresponds to the depth of recursion based on the input value n.
Example:
- For n = 5 : Calls = 6 (5 recursive calls + 1 base case).
- For n = 10 : Calls = 11.

How to Determine Call Count
For functions like calculating a factorial:
- Recursive calls are made
n + 1times (including the base case). - Example:
factorial(n) = n x factorial(n - 1)
Forn = 5calls:
factorial(5)tofactorial(4)tofactorial(3)tofactorial(2)tofactorial(1)tofactorial(0).
Total = 6 calls.
- Recursive calls are made
For binary recursion (Fibonacci):
- Each call branches into two new calls, doubling the number of calls for each level.
- Example: Fibonacci sequence:
fib(n) = fib(n - 1) + fib(n - 2)
Forn = 5the function will make 15 calls due to repeated calculations.
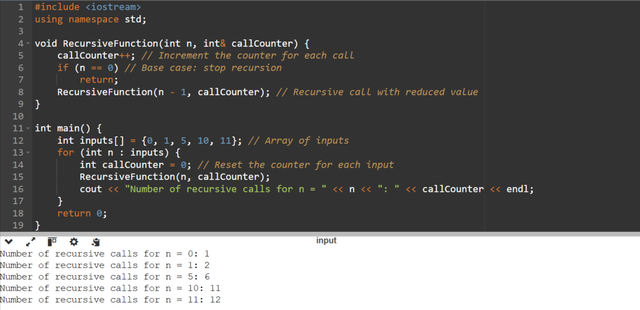
Key Observations
- Linear Recursion:
Call count = n + 1 or we can say that it is proportional to the input size. - Binary Recursion:
Call count grows exponentially as O(2n) . - Recursive Depth and Calls:
The depth of recursion directly relates to the number of calls unless the recursion involves branching.
Example Outputs for Factorial
| Input (n) | Number of Calls |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
| 5 | 6 |
| 6 | 7 |
| 7 | 8 |
| 8 | 9 |
| 9 | 10 |
| 10 | 11 |
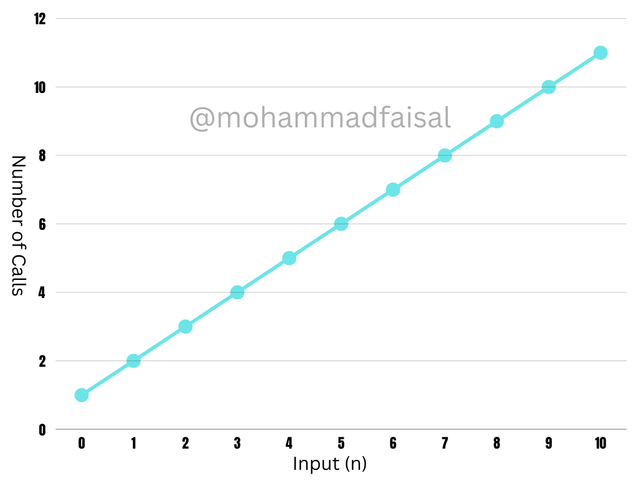%20(1).png)
Here you can see the graph of the relationship of the input and the number of calls. The graph shows a linear relationship between the input n and the number of the recursive calls(n+1). You can see that each additional input increases by one. So it represents straightforward nature of linear recursion.
Print numbers from 1 to n
As we know that in the recursion the function calls itself again and again. And now in order to print the numbers from 1 to n I will use recursive function. The function will repeatedly call itself and it will print the current number and in this way it will move closer to the base case.
Function: I will use printNumbers(int current, int n) function to print numbers from 1 to n using recursive call.
Parameters:
current: The current variable tracks the current number being printed. It starts at 1.n: It is the upper limit or you can say the input from the user. It determines the printing of the numbers until n.
Logic:
Base Case: If current > n then the recursion will be stopped using return.
Recursive Step: It prints the current number then call the function again for the next number by using current+1.
Recursive Code to Print Numbers from 1 to n
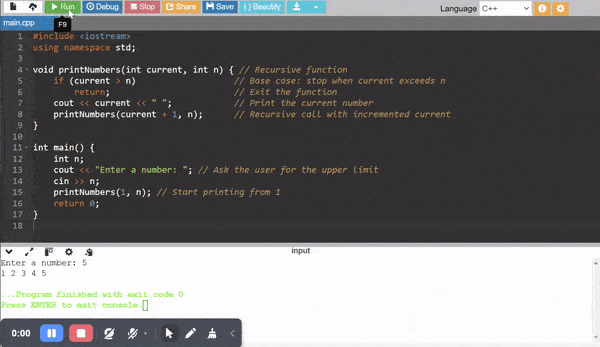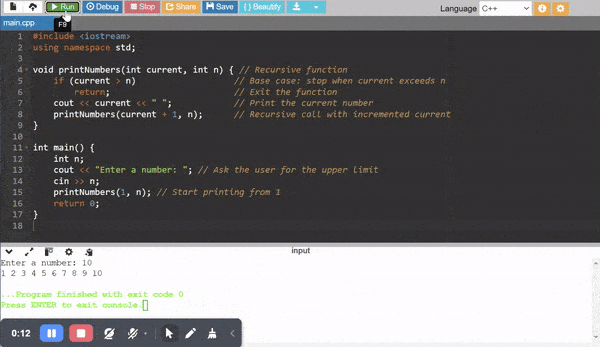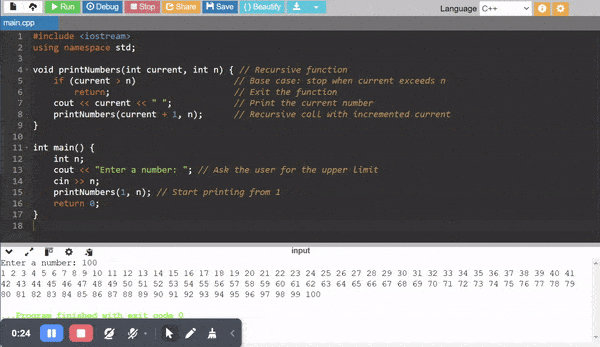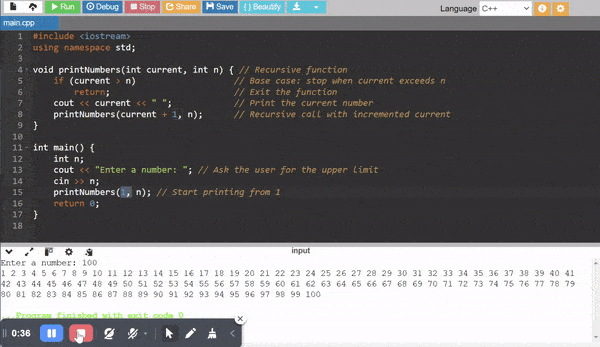
Explanation
- Base Case: When the current number exceeds (
n) then the recursion stops. - Recursive Call: The function calls itself with the next number (
current + 1). - Output: Numbers are printed in ascending order during the recursion.
If I am giving the input as n = 5 then it is printing theses numbers 1 2 3 4 5 starting from 1 and ending at n.
Execution Walkthrough
Let us see what happens when we take ( n = 5 ) for printing numbers from 1 to ( n ).
- The program begins with
printNumbers(1, 5). It prints1then callsprintNumbers(2, 5). - In
printNumbers(2, 5)it prints2then callsprintNumbers(3, 5). - This process repeats until
printNumbers(5, 5)prints5and callsprintNumbers(6, 5). - At
printNumbers(6, 5)the base caseif (current > n)is satisfied and recursion stops.
Call Stack Visualization
Each function call is added to the call stack and functions are removed in reverse order once the base case is reached.
Initial Call
printNumbers(1, 5)
Recursive Calls
- Prints
1, then callsprintNumbers(2, 5). - Prints
2, then callsprintNumbers(3, 5). - Prints
3, then callsprintNumbers(4, 5). - Prints
4, then callsprintNumbers(5, 5). - Prints
5, then callsprintNumbers(6, 5). - Base case is reached and the recursion stops.
Call Stack at Each Step
| Step | Call Stack | Output |
|---|---|---|
| Start | printNumbers(1, 5) | 1 |
| Recursive Call | printNumbers(2, 5) | 1 2 |
| Recursive Call | printNumbers(3, 5) | 1 2 3 |
| Recursive Call | printNumbers(4, 5) | 1 2 3 4 |
| Recursive Call | printNumbers(5, 5) | 1 2 3 4 5 |
| Base Case | printNumbers(6, 5) | — |
Print numbers from n to 1
This task is similar with the previous one but here we need to print the number in the descending order. So for this I will again use a recursive process where the function repeatedly calls itself and each time it reduces n until the base case is reached.
Recursive Code to Print Numbers from n to 1.
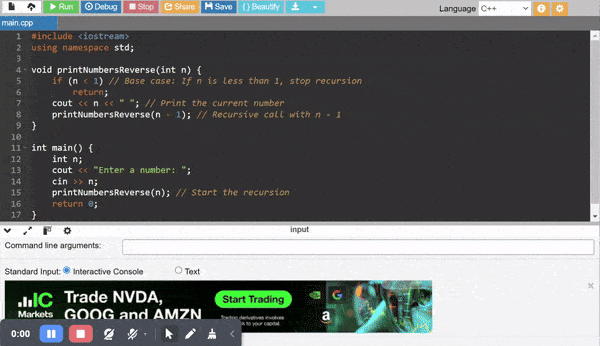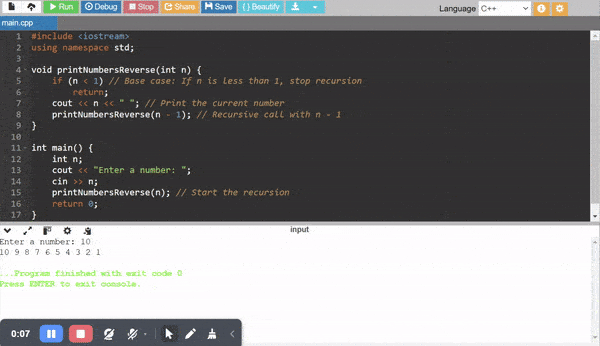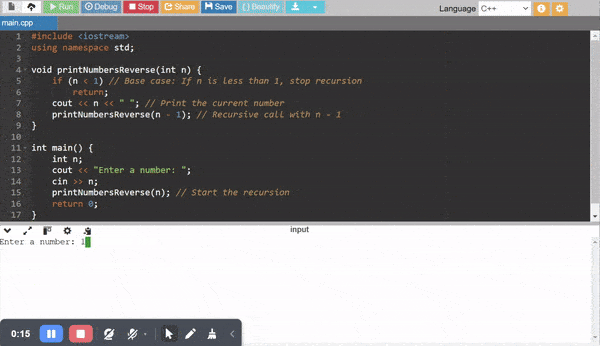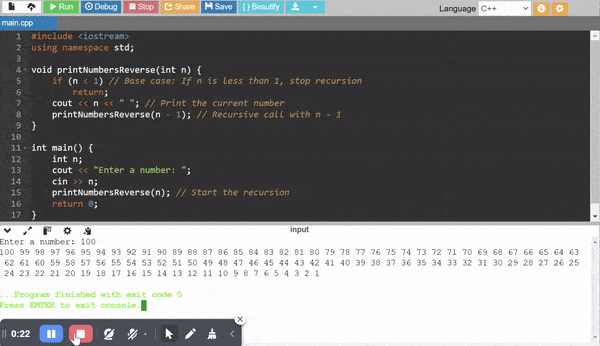
Detailed Explanation
Recursive Function:
- The function
printNumbersReverse(int n)takesnas input. - It first checks the base case:
if (n < 1). Ifnbecomes less than 1 then the recursion stops. So further function calls are not made in this case. - Before making the recursive call it prints the current value of
n. - Then it calls itself with
n - 1.
- The function
Base Case:
- Recursion must always have a termination condition. Here in this base case is when
nbecomes less than 1 (if (n < 1)). - When the base case is reached then the function simply stops and no further output is generated.
- Recursion must always have a termination condition. Here in this base case is when
Recursive Step:
- The function calls itself with a reduced value of n (
n - 1). - Each recursive call performs the same task. It prints
nand calls the function again with (n - 1). - This continues until (
n) reaches 1.
- The function calls itself with a reduced value of n (
Printing in Reverse:
- Since the current number is printed before the recursive call then the numbers are displayed in descending order.
Execution Walkthrough
Let us see what happens when we take n = 5.
- The program begins with
printNumbersReverse(5). It prints5then callsprintNumbersReverse(4). - In
printNumbersReverse(4)it prints4then callsprintNumbersReverse(3). - This process repeats until
printNumbersReverse(1)prints1and callsprintNumbersReverse(0). - At
printNumbersReverse(0)the base caseif (n < 1)is satisfied and recursion stops.
Call Stack Visualization
Each function call is added to the call stack and functions are removed in reverse order once the base case is reached.
Initial Call
printNumbersReverse(5)
Recursive Calls
- Prints
5, then callsprintNumbersReverse(4) - Prints
4, then callsprintNumbersReverse(3) - Prints
3, then callsprintNumbersReverse(2) - Prints
2, then callsprintNumbersReverse(1) - Prints
1, then callsprintNumbersReverse(0) - Base case is reached and the recursion stops.
Call Stack at Each Step
| Step | Call Stack | Output |
|---|---|---|
| Start | printNumbersReverse(5) | 5 |
| Recursive Call | printNumbersReverse(4) | 5 4 |
| Recursive Call | printNumbersReverse(3) | 5 4 3 |
| Recursive Call | printNumbersReverse(2) | 5 4 3 2 |
| Recursive Call | printNumbersReverse(1) | 5 4 3 2 1 |
| Base Case | printNumbersReverse(0) | — |
Write a function to calculate the sum of two numbers a+b. Do not use the a+b calculation directly. First perform this task using a loop (1 point), maybe it will tell you how to use recursion here and perform this task.
Sum of Two Numbers Without Using the + Operator
We can compute the sum without using +. So in order to calculate the sum of two numbers without directly using + operator we can use an alternative approach that performs the addition process. This exercise is both a logical challenge and an opportunity to explore the basic programming concepts like loops and recursion.
We can break down this problem into smaller tasks such as:
- Incrementing or decrementing one number (
a) step by step based on the second number (b) until the sum is achieved. - Representing the process programmatically using loops or recursive function calls.
This approach shows how iteration and recursion solve a problem systematically by reducing it into manageable steps. And it shows how we can ultimately find the solution without directly relying on predefined operators.
1. Using a Loop
The loop uses the addition process by repeatedly changing the values of a and b until b reaches zero. I will use a while loop for this task. It will ensure that the program will continuously run until the condition remains true. And I will use if-else statement to define the conditions. Here is the C++ code to calculate the sum of the 2 numbers by using loop and without using + operator.
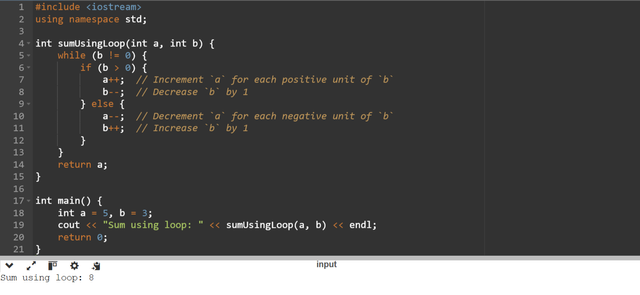
Explanation
- The loop modifies
aby incrementing it. It reducesbtowards zero. - For positive
b,aincreases andbdecreases. For negativeb,adecreases andbincreases. - When
breaches0then the sum of the original numbers is stored ina.
Example Walkthrough
Input: a = 5, b = 3
- Start:
a = 5,b = 3. - Iteration 1: Increments
ato 6 and decrementsbto 2. - Iteration 2: Increments
ato 7 and decrementsbto 1. - Iteration 3: Increments
ato 8 and decrementsbto 0. - Output:
a = 8.
2. Using Recursion
Recursion breaks the problem into smaller and self similar sub problems. Each recursive call processes one unit of the sum. And in this way it gradually moves closer to the base case. So here in order to calculate the sum of the 2 numbers by using recursive function C++ code is given below:
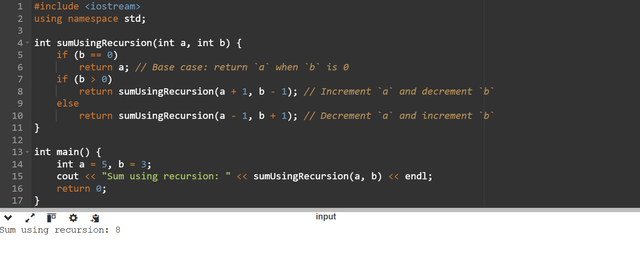
Explanation
- Base Case: If
b == 0then it returnabecause the addition is complete. - Recursive Step:
- For positive
bthe program incrementsaby 1 and decrementsbby 1. - For negative
bthe program decrementsaby 1 and incrementsbby 1.
- For positive
- The recursion continues until the base case is reached and the function resolves step by step to provide the final sum.
Example Walkthrough
Input: a = 5, b = 3
sumUsingRecursion(5, 3)callssumUsingRecursion(6, 2).sumUsingRecursion(6, 2)callssumUsingRecursion(7, 1).sumUsingRecursion(7, 1)callssumUsingRecursion(8, 0).sumUsingRecursion(8, 0)returns 8.
Observations
Recursive Functions use memory on the call stack. It grows with the number of calls. This can lead to stack overflow for very large values of
b.Loops are more memory efficient because they avoid additional stack overhead.
Both approaches produce the same result but their implementation and performance characteristics differ from each other.
Printing a String Character by Character in C++
When we work with the strings in C++ then it is crucial to understand how character arrays function. When we declare a string as char s[] = "recursia";. It is stored as an array of characters. And here s represent the address of the first character. By using this address we can access each character turn by turn.
Key Concepts
Array Name as a Pointer:
- The name
sholds the address of the first character of the array. s[0]gets the first character directly while*sdereferences the pointer to fetch the same value.
- The name
Accessing Characters:
- Array Indexing: Access each character using
s[i]. - Pointer Arithmetic: Increment the pointer to move to the next character by using
*(s + i).
- Array Indexing: Access each character using
Null Terminator:
- C++ strings (as
chararrays) are terminated with\0. They ensure safe traversal without going out of bounds.
- C++ strings (as
Approaches for Character-by-Character Printing
Using Array Indexing
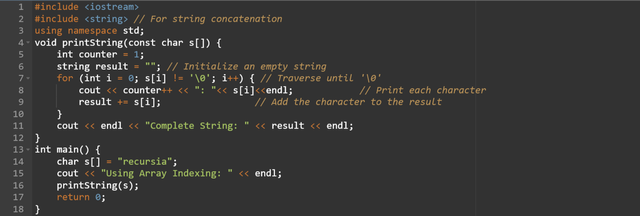
We can print the string character by character by using the loop and array index. The program iterates through the array using a loop. It checks for the null terminator. So how we can print the string character by character using the array index and loop and by terminating the loop by null terminator here is the C++ code:
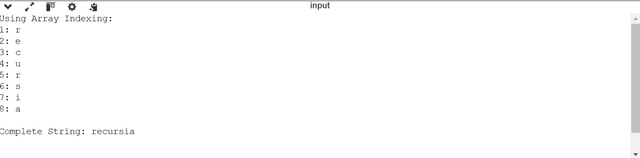
Here:
- The program is first printing all the characters in the string one by one.
- The program is returning the complete string by concatenating all the characters of the string.
- The
countervariable starts at 1 and increments on each iteration. - The
cout << counter++ << ": " << s[i] << endl;outputs each character prefixed by its index. - The
resultstring collects all characters from the array usingresult += s[i];. - After the loop the
resultstring is printed as the complete concatenated string.
Using Pointer Arithmetic
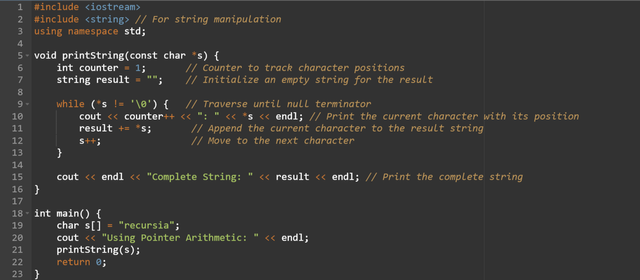
We can print the string character by character by using the pointer arithmetic. Here we will traverse the string using the pointer arithmetic. And each character will be accessed by the dereferencing the pointer. As the pointer moves through the string the program will print each character to a result variable. Once all the characters are processed then the complete string will be displayed.

Here:
- The
whileloop iterates through each character of the string using pointer arithmetic. - The dereferenced pointer (
*s) gets the character at the current position. - Each character is added to
resultfor constructing the complete string. - The
counterensures every character is numbered for clarity.
Execution Walkthrough
Let’s analyze char s[] = "recursia";.
Step-by-Step Execution
| Index | Pointer (s + i) | *Value at Address (s[i] or (s + i)) | Action |
|---|---|---|---|
| 0 | Address of 'r' | 'r' | Print 'r'. |
| 1 | Address of 'e' | 'e' | Print 'e'. |
| 2 | Address of 'c' | 'c' | Print 'c'. |
| 3 | Address of 'u' | 'u' | Print 'u'. |
| 4 | Address of 'r' | 'r' | Print 'r'. |
| 5 | Address of 's' | 's' | Print 's'. |
| 6 | Address of 'i' | 'i' | Print 'i'. |
| 7 | Address of 'a' | 'a' | Print 'a'. |
| 8 | Address of '\0' | Null terminator (\0) | Stop loop. |
Key Observations
Memory Access:
s[i]uses array indexing to fetch a value while*(s + i)uses the pointer directly.- Both methods result in the same output but differ in syntax.
Safety:
- The loop halts upon encountering
\0. It ensures that no memory beyond the string is accessed.
- The loop halts upon encountering
Performance:
- Pointer arithmetic can be slightly faster because it avoids indexing overhead but the difference is negligible.
Printing a String in Reverse Character by Character
In order to print a string in the reverse order we need to start from the last character of the string just before the null terminator \0. And then we need to work backward to the first character. The concept remains similar to traversing the string normally. But here the reverse logic will be applied.
Key Concepts
Finding the End of the String:
- We will use
strlen(s)to determine the length of the string in standard C++. - In another way we can also iterate through the string until we encounter the null terminator (
\0).
- We will use
Print Characters Backward:
- Here we will use array indexing with
s[length - 1]for the last character. - Alternatively we can use pointer arithmetic to decrement from the end.
- Here we will use array indexing with
Approaches for Reversed Character by Character Printing
Here I will discuss two approaches similar to the previous task. In the first approach I will use array indexing and then I will achieve it using pointer arithmetic.
Using Array Indexing
Start from the last character and decrement the index:
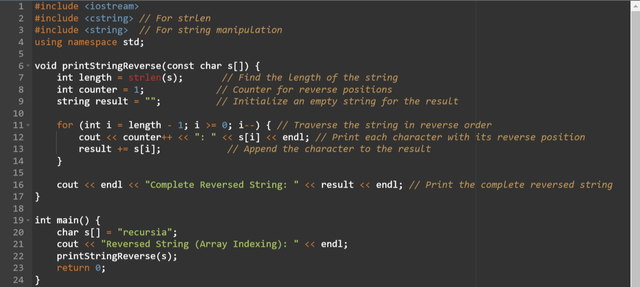

Here:
- The
forloop starts at the last index (length - 1) and moves towards the first index (0). This is the logic for the reverse approach. - Characters are printed one by one along with their reverse positions.
- The reversed string is constructed by pushed characters to the
resultstring. - The program ends by displaying the complete reversed string.
Using Pointer Arithmetic
In this approach we will start from the end of the string. And after each iteration we will decrement the pointer. We will do it until we reach to the first character of the string.
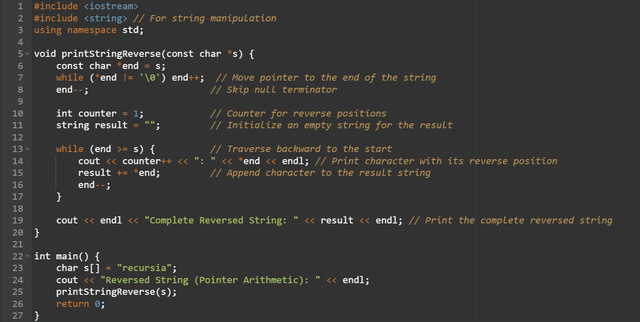

Here:
- The first
whileloop moves the pointer to the end of the string, just before the null terminator. - The second
whileloop iterates backward from the end of the string to the start, printing each character with its reverse position and accumulating it in theresultstring. - The final reversed string is displayed after the loop concludes.
Execution Walkthrough
Given the string char s[] = "recursia";:
Character Positions in Memory
| Index | Character | Address (Pointer) |
|---|---|---|
| 0 | r | s + 0 |
| 1 | e | s + 1 |
| 2 | c | s + 2 |
| 3 | u | s + 3 |
| 4 | r | s + 4 |
| 5 | s | s + 5 |
| 6 | i | s + 6 |
| 7 | a | s + 7 |
| 8 | \0 | s + 8 |
Reverse Printing
- Start from the last character
'a'(ats[7]or*(s + 7)). - Print each character while decrementing the index or pointer.
- Stop when reaching the first character (
s[0]or*s).
Comparison of Approaches
| Method | Description | Performance | Readability |
|---|---|---|---|
| Array Indexing | Uses indices to directly access characters. | Efficient | Simple for beginners |
| Pointer Arithmetic | Uses pointer manipulation to traverse backward. | Slightly faster | Advanced-level |
Note: I have used Onlinegdb Compiler to compile the code in C++ language.