SLC21 Week6 - Programming Games&Puzzles (part 2)
Hello steemians,
Here is my homework for SLC21 Week 6, with the corresponding tasks assigned by @sergeyk!
.png)
What role do random numbers play in the computing world? How can they be transformed from "pseudo-random" to more random?
Random numbers play a crucial role in many areas of computing, providing the unpredictability and diversity essential to diverse applications such as cryptography, simulations, video games and software testing; in cryptography, they are essential for generating secure keys to protect data and ensure secure communications, without this randomness it would be almost impossible to achieve the required level of security, as predictable numbers could easily compromise encrypted systems.
In simulations and modeling, random numbers replicate unpredictable events, creating realistic scenarios that mimic natural phenomena or real-world situations; these numbers are as essential in areas as simple as games or as complex as models scientific data such as weather forecasts, ensuring unpredictable behavior and relevant results.
In video games they improve the experience by introducing varied behaviors, unique environments and unpredictable challenges, making each game different, similarly, for software testing they generate random data, helping to detect bugs by exposing programs to a multitude of unanticipated conditions.
The numbers produced by the algorithms are referred to as "pseudo-random", because they are generated by deterministic formulas that produce predictable sequences if the initial seed is known, while this may be useful for debugging or testing, it limits their usefulness in contexts requiring true chance.
And to make these numbers closer to absolute randomness, we can use a dynamic seed such as the system clock time(0) which produces a single seed based on the current time that guarantees constant variation, we can also combine external sources of entropy such as mouse movements or hardware generators that collect physical noise to produce unpredictable numbers.
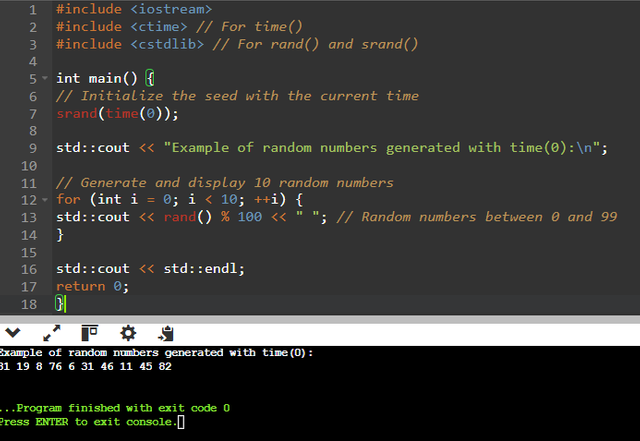
In this example, we use time(0) to initialize the pseudo-random number generation seed, the function srand(time(0)) allows us to initialize the random number generator using the current time As a starting point, this means that each time the program runs, the generated sequence of numbers will be different, unless the program runs at the same second, because time(0) returns the number of elapsed seconds since January 1, 1970. The rand() function is then used to generate pseudo-random numbers, in this example we use the expression rand() %100 to limit the numbers generated to a range of 0 to 99, but this can be adjusted as needed, when the program is run a unique sequence of numbers is produced each time, illustrating how using time(0) adds random dynamics to the generating pseudo-random.
Write a random number generator. Explore it.
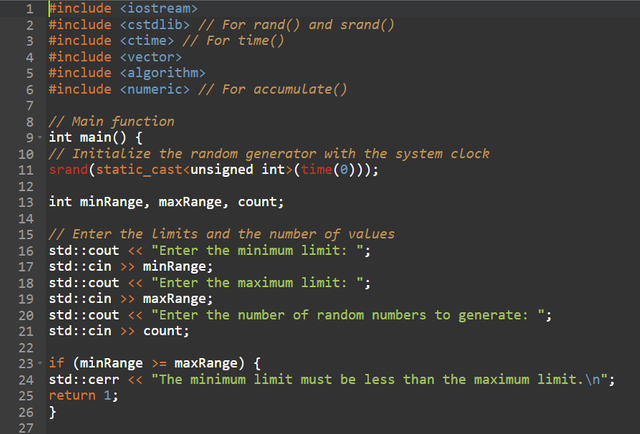
The program starts by including the necessary libraries, including <cstdlib> to use the rand() and srand() functions, and <ctime> to initialize the random generator with the system clock, the user is prompted to enter three values: the minimum limit, the maximum limit and the number of random numbers to be generated, a check is performed to ensure that the minimum limit is much lower than the maximum limit, then a loop generates the random numbers using a formula for the adjust across terminals specified, with these numbers stored in a vector.
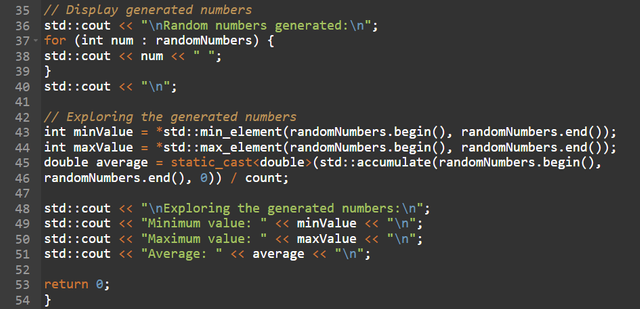
Once the generation is complete, the generated numbers are displayed, the program then explores this data to extract the minimum value, maximum value and average, the minimum and maximum value are obtained using the std::min_element and std::max_element, which traverse the vector, the average is calculated by adding all the numbers in the vector with std::accumulate, then dividing by the number of values generated.

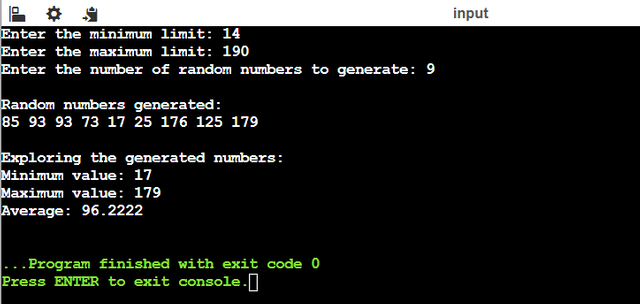
Example of execution
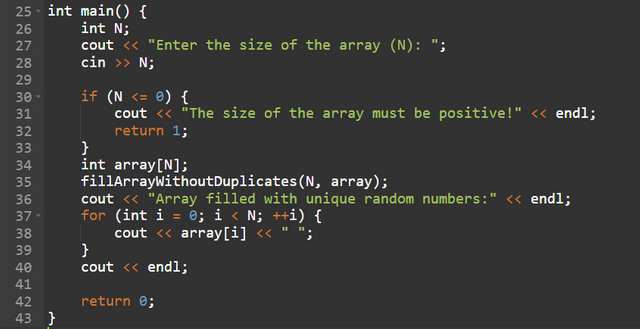
3. "Deck of Cards": Find multiple ways to fill an array 1...N without repetition. (5 points)
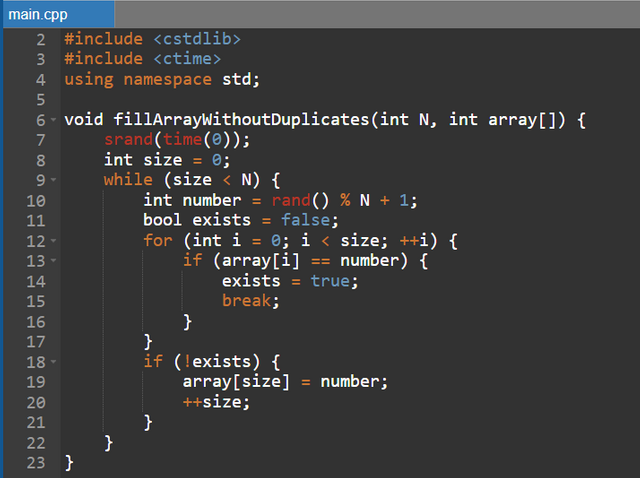
To create an array containing all the numbers between (1) and (N) in random order, the basic idea is to start with an empty or pre-populated array and manipulate the values so that they are arranged randomly without duplicate.
In one approach the array is randomly populated by choosing numbers between (1) and (N), for each new number a check is performed to ensure it is not already in the array, thus avoiding duplicates, this involves iterating through existing elements to see if the new number is already present.
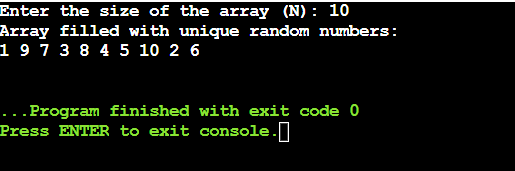
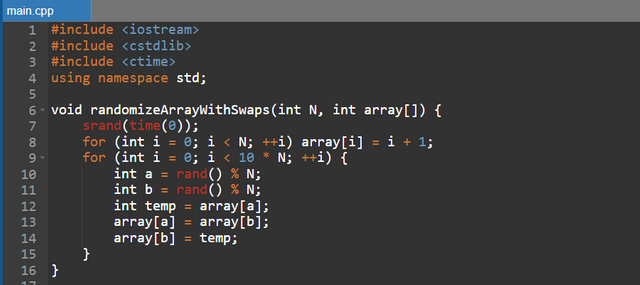
Another approach is to directly fill the table with values from (1) to (N), then, to randomize these values, several exchanges are made between two randomly chosen positions, at each iteration, two indices of the table are selected at happenstance and their values are exchanged.
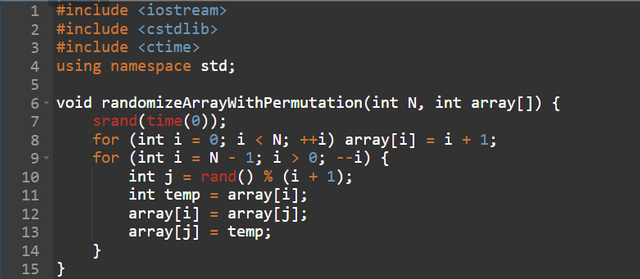
A more structured technique is to iterate through the array from right to left, at each step a random index is chosen and the two values of the current position and the random index are swapped, this ensures that each permutation of the array is equally likely , whilst preserving the uniqueness of values.
Build a table of the number of operations for generating a deck of N cards for your methods.
First Approach
In this method, each number is randomly generated, and its uniqueness is verified before adding it to the deck.
- Random number generation: This operation is performed at every iteration.
- Duplicate checking: For each potential addition, all previously added elements are scanned to ensure there are no duplicates.
- Adding to the deck: Once validated as unique, the number is added to the deck.
The total number of operations depends on the current size of the deck as it fills. For a deck of size ( N ), the total cost can be approximated as a quadratic sum:
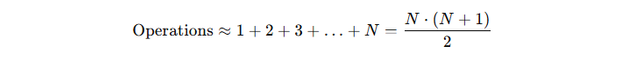
Second Approach
In this method, the deck is first filled sequentially with values from ( 1 ) to ( N ), followed by random shuffling.
- Sequential filling: This step requires exactly ( N ) operations because each position in the deck is assigned a value.
- Random shuffling: The deck is traversed from right to left (( N - 1 ) iterations). At each step:
- A random index is chosen (1 operation).
- The values at the current and random indices are swapped (1 operation).
The total number of operations is:
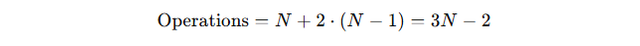
Third Approach
In this method, the deck is filled sequentially with values from ( 1 ) to ( N ), followed by repeated random swaps a fixed number of times (( 10 \cdot N )).
- Sequential filling: Similar to the second approach, this step requires ( N ) operations.
- Repeated swaps: For each swap:
- Two random indices are chosen (2 operations).
- The values at the two indices are swapped (1 operation).
The total number of operations is:
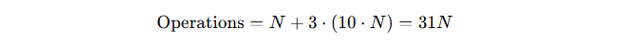
Here is a table comparing the number of operations needed to generate a shuffled deck for values of ( N ) ranging from 4 to 8:
| ( N cards) | Total Operations (First Approach) | Total Operations (Second Approach) | Total Operations (Third Approach) |
|---|---|---|---|
| 4 | 10 | 10 | 84 |
| 5 | 15 | 13 | 105 |
| 6 | 21 | 16 | 126 |
| 7 | 28 | 19 | 147 |
| 8 | 36 | 22 | 168 |
Thank you very much for reading, it's time to invite my friends @analp, @crismenia, @eliany to participate in this contest.
Best Regards,
@kouba01

💯⚜2️⃣0️⃣2️⃣4️⃣ This is a manual curation from the @tipu Curation Project
@tipu curate
Upvoted 👌 (Mana: 2/7) Get profit votes with @tipU :)