Uso de la derivada en el cálculo de costos // Aplicación en la Economía
En el artículo anterior hice referencia a como la derivada da respuesta a los problemas presentes en la física, tal es el caso de los ritmos o velocidades de cambio, y es que no solamente podemos ver evidenciadas una sola aplicación de esta hermosa herramienta matemática como lo es la deriva, también podemos aplicar el uso de la derivada a una infinita serie de problemas, entre los que está el cálculo de costos en el área de la economía.
En economía, la variación de una cantidad con respecto a otra puede describirse mediante el concepto de variación promedio o del concepto de variación marginal.
Concepto de variación promedio y variación marginal
La variación promedio expresa la variación de una cantidad sobre un intervalo de valores de una segunda cantidad.
La variación marginal es la variación instantánea de la primera cantidad que resulta de una pequeña unidad de variación de la segunda cantidad.
Costo promedio y costo marginal
Suponga que C(x) es el costo total para producir x unidades de un artículo. La función C se denomina función de costo total.
En circunstancias normales x y C(x) son positivos. Debido a que x representa la cantidad de unidades de un artículo, usualmente x es un número entero no negativo. Sin embargo, a fin de aplicar el Cálculo, se supondrá que x es un número real no negativo para satisfacer los requerimientos de continuidad de la función C.
El costo promedio de producción de cada unidad de un artículo se obtiene al dividir el costo total entre el número de unidades producidas.
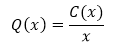 ; Q se conoce como función de costo promedio.
; Q se conoce como función de costo promedio.
Ahora podemos suponer que el número de unidades producidas es 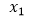 , y que se incrementa en ∆x. Entonces la variación del costo total está determinado por
, y que se incrementa en ∆x. Entonces la variación del costo total está determinado por 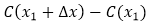 , y la variación promedio en el costo total con respecto a la variación del número de unidades producidas está dado por
, y la variación promedio en el costo total con respecto a la variación del número de unidades producidas está dado por 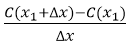 .
.
Los economistas utilizan la derivada para el cálculo de costos, utilizando el término costo marginal para el límite de este cociente cuando ∆x tiende a 0. Suponiendo que el límite existe. Este límite, que es la derivada de C en 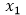 , establece que el costo marginal, cuando
, establece que el costo marginal, cuando 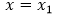 , está dado por
, está dado por 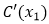 , si existe, La función C' recibe el nombre de función de costo marginal, y
, si existe, La función C' recibe el nombre de función de costo marginal, y 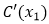 puede interpretarse como la tasa de variación del costo total cuando se producen
puede interpretarse como la tasa de variación del costo total cuando se producen 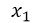 unidades de cierto artículo.
unidades de cierto artículo.
Ejemplo para el cálculo de costo marginal
Una empresa productora de tubos de perforación petrolera fabrica tubos de perforación, el costo total para la producción de esos tubos viene expresada por la siguiente función de costo total (C(x)):
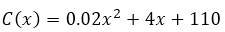
C(x) se mide en dólares. Calcular:
a. La función de costo marginal.
b. El costo marginal por cada tubo de perforación cuando se fabrican 50 tubos.
c. El número de dólares del costo real de fabricación del tubo 51.
a. Para encontrar la función de costo marginal C'(x), solo hay que derivar la función de costo total C(x). La derivada de C(x) la vamos a conseguir aplicando la derivación por las reglas básicas de derivación.
Como la función C(x) tiene la sumatoria de tres términos, aplicamos la siguiente regla básica de derivación:
[U+V+W]'= [U]'+ [V]'+ [W]'
Con lo que quedaría que:
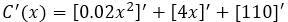
- Para derivar el término
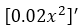 , aplicaremos la siguiente regla básica del múltiplo constante por la derivada de una potencia:
, aplicaremos la siguiente regla básica del múltiplo constante por la derivada de una potencia: 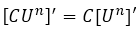 ; donde C= 0.02 y
; donde C= 0.02 y 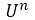 =
=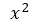 . De esta manera solo nos quedaría saber cuál es la derivada de
. De esta manera solo nos quedaría saber cuál es la derivada de 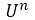 , por lo que es necesario que apliquemos la regla básica de derivación para funciones exponenciales del tipo
, por lo que es necesario que apliquemos la regla básica de derivación para funciones exponenciales del tipo 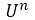 , con lo que podemos decir que
, con lo que podemos decir que 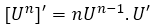 .
.
La derivada del término 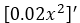 =
= 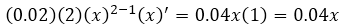
Para derivar el término
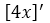 , lo que tenemos que saber es que la derivada de X es igual a 1, y que multiplicado por el múltiplo constante da como resultado igual a 4, lo que implica que
, lo que tenemos que saber es que la derivada de X es igual a 1, y que multiplicado por el múltiplo constante da como resultado igual a 4, lo que implica que 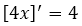
Para derivar el término
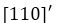 , lo que tenemos que saber que la derivada de una constante es cero, es decir
, lo que tenemos que saber que la derivada de una constante es cero, es decir 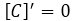 , por lo que
, por lo que 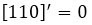 .
.
Finalmente la derivada de la función del costo total es igual a la suma de la derivada de los tres términos, con lo que se deduce que: 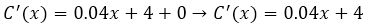
Para lo que podemos concluir que la función de costo marginal (C(x)) está definida por 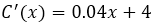
b. Para calcular el costo marginal por cada tubería de perforación que se produce cuando se hayan fabricado 50 tubos, lo que hay es que sustituir x=50 en la función de costo marginal C'(x), ya que x representa la cantidad de tubos fabricados, lo que implica que:
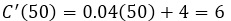
La tasa de variación del costo total, cuando se fabrican 50 tubos de perforación, es de 6 dólares por cada tubería que se fabrica.
c. El costo real de fabricación en dólares de la tubería 51, viene dado por [C(51)-C(50)], con lo que podemos realizar por separado el costo real de la fabricación del tubo 51 y 50, y la resta de los dos será el costo real de fabricación del tubo 51.
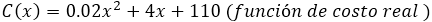
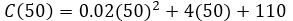
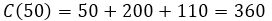
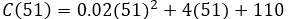
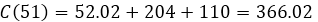
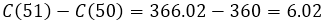
El costo real de fabricación del tubo 51 es de 6.02 dólares, podemos analizar que la diferencia de costo entre la tubería número 51 y 50 es de 0.02 dólares, esta discrepancia es debida a que el costo marginal es la tasa instantánea de variación de C(x) con respecto a una variación de una unidad de x, en consecuencia, C'(50) es el número aproximado en dólares del costo de fabricación de la tubería 51.
Conclusión y consideraciones
Los costos de determinado producto puede depender de muchos factores, entre los que pueden estar los procesos inflacionarios, el costo de los materiales de fabricación, personal involucrado en la fabricación. En el caso de la presente publicación se hace concluyente que los costos de fabricación de determinado producto que varíe con respecto a la producción, son muy importantes de determinar cuándo se tiene una diversidad considerable en los índices de producción, estos costos denominados marginales se analizan de una manera optimizada mediante el uso y aplicación de la derivada.
En el caso del ejercicio expresado en este artículo cabe destacar que la función de costo real total es una parábola que se basa en el modelo de ley de los rendimientos decrecientes, es por ello que nunca veremos una función de costo real total que no sea una función cuadrática.
En consecuencia del costo marginal de producción, este nos proporciona el precio exacto a partir del cual se pueden obtener beneficios en base a lo que a ganancias se refiere, eso sí teniendo en cuenta que el costo marginal alcance el punto muerto o de rentabilidad.
Es importante para todo aprendiz que desee aplicar el uso de la derivada en el costo real y marginal de un producto, que se disponga de la función de costo real total, en caso de no disponerla se puede aproximar por cualquier modelo matemático (completación de cuadrados, Sistemas de ecuaciones, cualquier herramienta algebraica de aproximación de cuadrados) siempre teniendo en cuenta que esta función tiene que ser cuadrática, una vez analizada y entendida la función de costo real es importante poseer la destreza necesaria para poder realizar la derivada de dicha función.
Para el caso del ejercicio de cálculo del costo marginal para cuando se fabricaron 50 tuberías, quiero adicionar el gráfico de la función de costo total de producción, usando el software de geogebra 5.0
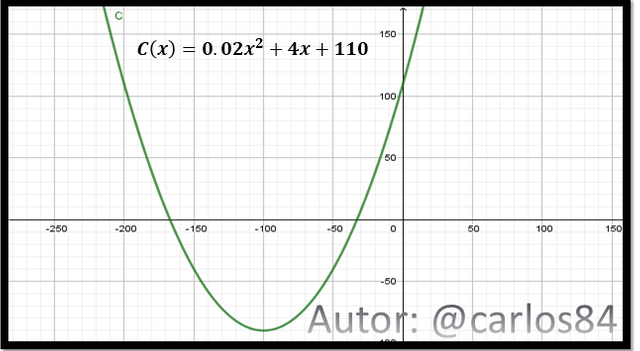
Del gráfico y la función de costo total real se puede hacer varias observaciones, una de ellas es que cuando no se fabrica ningún tubo se tiene un costo de 110 dólares.
- Todas las ecuaciones y fórmulas plasmadas en este artículo fueron realizadas por mi persona utilizando las herramientas de inserción de ecuaciones en Microsoft Word.
Referencias bibliográficas consultadas
Cálculo con geometría analítica. Autor: Ron Larson y Robert P. Hostetler. 8va edición. Editorial Mc Graw Hill. Volumen I. México 2006.
El Cálculo. Autor: Louis Leithold. 7ma edición. Editorial Oxford. México 1998.
"Para toda aquella persona que le apasiona la matemática, física, química, biología, educación e ingeniería, le recomiendo la etiqueta de #stem-spanol, es una comunidad que valora el contenido intelectual y académico de calidad, conservando siempre la originalidad de las publicaciones, por lo que se recomienda a todos aquellos amigos de steemit que deseen publicar utilizando esta etiqueta a no cometer plagio."

¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Hola @carlos84, excelente publicación, en efecto en las escuelas de economía, contaduría el estudio del Cálculo Diferencial e Integral es parte de pensum de estudios obligatorio de los cursantes de estas carreras, en tanto que los saberes de estas áreas de la Matemática les proveen de herramientas necesarias para el estudio de fenómenos asociados a las fluctuaciones del mercado y al mismo tiempo realizar predicciones que generen provecho a la sociedad, de allí la importancia de tu aporte para esta comunidad, que en adición viene a mostrar una de las innumerables formas en que la Matemática apoya a la humanidad y su progreso, te felicito, saludos fraternos!!
Hola mi estimada y apreciada @reinaseq. Gracias por el apoyo brindado, muy acertado y propicio tu comentario, el cálculo diferencial e integral es muy apropiado para aplicaciones en el ámbito económico, muy pronto estare subiendo artículos en el área del cálculo integral. Saludos y en espera de tener la dicha de leer y aprender sobre tus temáticas en matemática.