¿Lógica?
Hola amigos de steemit, a continuación, un poco de lógica.
¿Lógica?
Esta es una palabra que manejamos a menudo, haciendo referencia al sentido común cuando la usamos, pero en realidad abarca mucho más que esto, a tal punto de ser considerada una ciencia.
La lógica es una ciencia formal y rama estricta de la Filosofía y la Matemática, estudia los principios de demostración e inferencias válidas (proceso por el cual se derivan conclusiones partiendo de premisas), falacias, paradojas y la noción de verdad. Se trata de una ciencia que no tiene contenido, pues atiende solo el aspecto estructural de las inferencias, es decir; trata del estudio de los métodos y principios utilizados para distinguir el razonamiento correcto, del incorrecto.
La lógica como disciplina ha sido estudiada a nivel histórico desde civilizaciones antiguas como la India, China, Persia y Grecia. Pero es Aristóteles (384 a.c. – 322 a.c.) quien la define como una ciencia por primera vez, y elaboró leyes para un correcto razonamiento silogístico, quizás por esto es considerado el padre de la lógica, Aristoteles la describe de la siguiente manera:
La lógica es la ciencia de la demostración, porque se preocupa de dar reglas para alcanzar la verdad de evidencia inmediata, que conocemos por medio de la demostración.

Aristóteles aporta a la lógica la introducción del uso de variables, las proposiciones por su cantidad y su cualidad, el raciocinio deductivo, las formalizaciones de la lógica y el desarrollo silogístico. Sin embargo, sus predecesores desarrollaron y cultivaron la inferencia y la prueba en los diferentes debates que por aquel tiempo realizaban los filósofos. A finales del siglo XIX, la lógica tuvo una formalización simbólica relacionándose estrechamente con las matemáticas, a tal punto que ya para el siglo XX paso a conocerse como lógica matemática. El precursor de esta lógica es Guillermo G. Leibniz quien introdujo el cálculo lógico llamado “Mathesis Universalis” que fuese operacionalmente mecánico, inequívoco y no cuantitativo, lo que permitió acabar con todas las disputas y controversias de aquel entonces. También desarrolló el cálculo de la Lógica Proposicional. Euler es otro de los precursores de la Lógica Matemática, introdujo los diagramas que llevan su nombre para ilustrar geométricamente los silogismos.
Su importancia radica en que impulsa la capacidad racional y critica de las personas, ayuda con la correcta interpretación de los contenidos del lenguaje, contribuye a analizar de forma coherente los contenidos científicos, y también en el desarrollo tecnológico en especial con la cibernética e informática.
A continuación les plantearé un enigma, uno que recuerdo de cuando comencé mis estudios universitarios.
Uno de los contenidos a tratar en clase de Algebra (Una de mis favoritas) era este, la lógica, fundamental para un matemático, y en medio de su clase magistral recuerdo que el profesor nos hablo de enigmas, acertijos y paradojas y la importancia de la lógica para solucionar dichos problemas, fueron varios, pero este siempre lo recuerdo, era un reto en aquel entonces, en donde no era muy común estudiar a través de Google o videos de Youtube, jejejeje. Y hoy te lo propongo a ti.
Se trata de un enigma dentro de otro. Espero pienses un poco antes de ver la solución y dejes tu razonamiento al respecto en los comentarios, ¡no hagas trampa! (al finalizar, la solución).
“Los 3 sabios y los 5 sombreros”
A tres sabios consejeros uno de los cuales era ciego, se les propone un enigma para probar dicha sabiduría. De eso dependerían sus cabezas. A éstos los colocan en una habitación de tal manera que cada uno podía visualizar a sus compañeros. Se disponen de cinco sombreros, tres blancos y dos negros. Se les colocara a cada sabio uno de estos sombreros en lo alto de su cabeza, de tal manera que serán capaces de ver el sombrero que lleva su compañero pero no el suyo. A continuación proceden a colocarle los sombreros a cada uno, siendo los tres sombreros utilizados blancos y los otros dos negros fueron guardados.
El reto consiste en decir en un lapso determinado de tiempo el color del sombrero que llevan y justificar como lo han deducido. Esto se haría de forma individual sin que los compañeros restantes puedan escuchar. El primero en acertara terminaría con el reto.
Pues a continuación. Cumplido el lapso de tiempo sacan al primer sabio, quien no supo responder de qué color era su sombrero. De igual forma y en cuestión de minutos, sacan al segundo, quien tampoco respondió. Por último, al preguntarle al tercer sabio (que padecía ceguera), respondió para sorpresa de todos los presentes, dando su respectivo razonamiento y resultando cierta dicha respuesta.
La pregunta para usted es: ¿De qué color era el sombrero? Y ¿Como supo la respuesta correcta?
Y mientras ustedes piensan, seguimos con lo nuestro.
Tipos de lógica
- Existen varias pero nos adentraremos en una en particular más adelante.
- Lógica formal o Aristotélica, lógica antigua y de la cual derivan todas.
- Lógica proposicional, simbólica o matemática, dirigida al estudio de la validez de los argumentos y proposiciones usando un lenguaje formal y simbólico.
- Lógica informal, centrada en el lenguaje y el mensaje de los argumentos, su objeto de estudio es la forma de argumentar para obtener el resultado deseado. La lógica informal da validez a los argumentos lógicos que resultan más coherentes entre otros que tienen una estructura argumentativa más débil.
- Lógica computacional, es la lógica matemática, aplicada a la computación, usada en diferentes paquetes y lenguajes de programación como Prolog
Lógica Proposicional, Simbólica o Matemática
Las ciencias formales están constituidas por un conjunto de proposiciones (enunciados de los que se pueda afirmar su veracidad o falsedad) denominadas analíticas, su veracidad o falsedad dependen de un raciocinio lógico. La lógica proposicional es aquella que estudia las variables proposicionales, sus implicaciones, evaluaciones de verdad y en algunos casos su nivel absoluto de verdad.
Algunas proposiciones suelen ser largas, por lo que resulta tedioso escribirlas. Por ello, se hace uso de un lenguaje simbólico, estas proposiciones se suelen representar por letras como P, Q, R, S, etc.
Existen conectivos u operadores lógicos que permiten formar proposiciones compuestas, aquellas formadas por varias proposiciones. Los operadores o conectores básicos son:

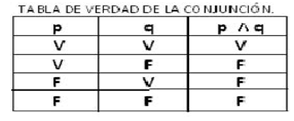
- Conjunción (operador “y”): Se utiliza para conectar dos proposiciones que se deben cumplir para que se pueda obtener un resultado verdadero. Se le conoce como multiplicación lógica y su símbolo es ∧.
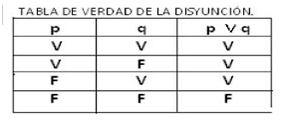
- Disyunción (operador “o”): Con este operador se obtiene un resultado verdadero cuando alguna de las proposiciones es verdadera. Se conoce como suma lógica y su símbolo es ∨.
- Negación (operador “no”): Su función es negar la proposición. Esto significa que sí alguna proposición es verdadera y se le aplica el operador no, se obtendrá su negación (falso) y viceversa, su símbolo es ¬.
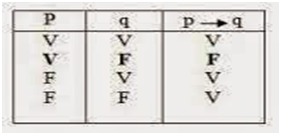
- Condicional o implicación (operador “entonces”): Es aquella que está formada por dos proposiciones (simples o compuestas), de tal manera que una implica la otra, y su símbolo es →.
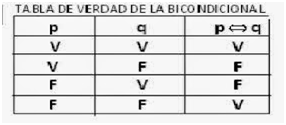
- Bicondicional o doble implicación (operador “si y solo si”) Es una doble implicación, cuyo símbolo es ↔.
Tablas de verdad
También conocida como tabla de valores de verdad, desarrollada por el filosofo, lógico y científico, Charles Sanders Peirce en 1880, es una tabla que muestra el valor de verdad (veracidad o falsedad) de una proposición, es un dispositivo para demostrar ciertas propiedades lógicas y semánticas de enunciados del lenguaje del cálculo proposicional.
Los valores de verdad que se le puede dar son las dos posibilidades que se tiene: verdadera (que se denotará por V y se dirá que su valor de verdad es V) o falsa (que se denotará por F y se dirá que su valor de verdad es F)..El valor de verdad de una proposición compuesta depende exclusivamente de los valores de verdad de las proposiciones simples que aparecen en ella.
A continuación se presentan las tablas de verdad para los conectivos lógicos: Siendo “p” y “q” proposiciones.
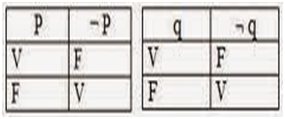
¿Tautología, Contradicción?
Aquella proposición (compuesta) que es cierta para todos los valores de verdad de sus variables, se le denominan tautologías, y son muy importantes en Lógica Matemática ya que se consideran leyes en las cuales se puede apoyar para realizar demostraciones. Mientras que aquella proposición que siempre es falsa para todos los valores de verdad, se le conoce como contradicción.
¿Sabías que?

Howard Gardner, psicólogo estadounidense, planteo la teoría de las inteligencias múltiples, realizando una clasificación de la misma en ocho tipos; entre las cuales se encuentra la inteligencia lógico-matemática, vinculada a la capacidad para el razonamiento lógico y la resolución de problemas matemáticos. La rapidez para solucionar este tipo de problemas es el indicador que determina cuánta inteligencia lógico-matemática se tiene, proporciona método, orden y sentido a nuestras acciones y/o decisiones. Según Gardner, los test de cociente intelectual (IQ) se fundamentan en este tipo de inteligencia. Ésta parece encontrarse principalmente en el hemisferio izquierdo, el hemisferio de la lógica por antonomasia. Se pone en marcha cuando nuestro cerebro debe relacionar datos de manera cruzada y procesarlos para obtener un resultado o una combinación de resultados. Dicha inteligencia se puede ejercitar practicando y analizando problemas exigentes, o simplemente resolviendo sudokus. Los que sobresalen en este tipo de inteligencia, son los científicos, economistas, ingenieros y por supuesto, los matemáticos.
Esperando haber aportado un poco de información útil, y que además haya sido de su agrado, me despido dejándoles por supuesto, con la solución al enigma propuesto anteriormente, espero entiendan y disfruten. ¡Feliz día para todos!
Solución al enigma:
¡Mi sombrero es blanco! Respondió el tercer y último sabio en ser interrogado, siendo veraz dicha respuesta. ¿Como lo supo? Pues él razonó de esta manera:
Hay tres sombreros blancos y dos negros. Si el primer sabio hubiese visto en cada uno de nosotros los dos sombreros negros, habría dicho sin dudar que su sombrero era blanco. Como no respondió, entonces tenía dudas, generando así dos posibilidades:
- Vio dos sombreros blancos. (lo que implicaría que el suyo podía ser blanco o negro).Vio un sombrero blanco y uno negro. (implicando de igual forma que su sombrero podría ser negro o blanco).
De acuerdo a la primera posibilidad, entonces mi sombrero seria de color blanco, exclamo el invidente, siendo correcta mi respuesta. Si tomamos en cuenta ahora la segunda posibilidad, entonces, ¿quién tendría el sombrero negro? Yo no podría tenerlo deduje, pues de ser así, el segundo sabio al ver que el primero no supo contestar, aunado con el hecho de que yo tenía un sombrero negro, hubiese razonado de la siguiente manera:
“Veo que este sabio (ciego) lleva un sombrero negro. Si el mío también es negro, entonces el primer sabio hubiese respondido que el suyo era blanco, pero éste no supo responder, por lo tanto, el mío tiene que ser blanco”.
Pero al no haber respondido éste, entonces dudaba. Por lo tanto, mi sombrero no podía ser negro, y al no haber otras opciones deduje que mi sombrero es blanco. Fin, Jejeje.
vaya esto si es un contenido de calidad no como lo que veo en steemit diariamente Saludos y mis respetos mi apoyo con mi voto.
Buenas tardes, muchas gracias, me tome el atrevimiento de pasarme por su perfil y sus post son un mundo que descubrir, que bueno de verdad lo felicito y gracias por su opinión, es un honor, creo me quede corta.
Congratulations @carolina88! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Gracias. !Que alegría!
Hola, muchas gracias por el apoyo :)
Congratulations @carolina88! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Artículo para leerlo varias veces, y aplicar.
Hola, gracias por comentar :)