En el anterior artículo de La matemática de la música "La ubicación de los trastes", se hizo mención a las diferentes relaciones que existen entre una nota y el resto de las doce que comprenden una octava musical, a tales correspondencias se les llamó relaciones pitagóricas. En el presente artículo desarrollaremos el origen matemático de dichas proporciones.

Fuente de la imagen original

---

Relación pitagórica de las notas musicales.

       Se le conoce como relaciones pitagóricas de las notas musicales, a las establecidas por los seguidores de la escuela fundada por el filósofo y matemático griego Pitágoras de Sames, en el siglo IV a.C. A este grupo de matemáticos se les reconoce en la historia como Los Pitagóricos y fueron los primeros en relacionar la matemática con la música, de hecho, afirmaban que eran cuatros las disciplinas que proporcionaban el saber en su expresión máxima: la geometría como estudio de las magnitudes en reposo, la astronomía como estudio de las magnitudes en movimiento, la aritmética como estudio de los números en reposo y la música como el estudio de los números en movimiento. A este grupo de ciencias les llamaban Quadrivium.

       Vale destacar que la historia no cuenta con pruebas fehacientes de que haya existido Pitágoras, especialmente porque no se conoce una biografía de él realizada por algún contemporáneo, sin embargo quienes contaron su historia siglos después no dudaron de su existencia, por lo que se le atribuyen diversos estudios e invenciones.

       Uno de los trabajos atribuidos a Pitágoras fueron los análisis y descubrimientos realizados con el monocordio, instrumento musical de una cuerda que contaba con un elemento móvil capaz de fraccionar su longitud. Mediante los experimentos realizados con este dispositivo se pudieron determinar diferentes proporciones de longitud de cuerdas que generan notas que se manifiestan en consonancia.

Fuente

       Consonancia y disonancia.

       En armonía musical, se conoce como consonancia al efecto agradable y de correspondencia que causan en el espectador, dos o más sonidos simultáneos pero de distintas alturas, y disonancia a la sensación de tensión o desproporción que pudieran generar otros sonidos dentro de la octava.

       Una octava musical es una sucesión ascendente o descendente de siete notas o sonidos, más la primera que se repite en el otro extremo pero más aguda o grave. En ella se pueden manifestar intervalos (par de sonidos de distintas alturas) con mucha o poca consonancia y disonancia.

       En el ejemplo anterior, se puede apreciar las notas musicales implícitas en la octava de Do, cada una de ellas tiene su octava superior e inferior. Alterando algunas (con sostenidos o bemoles) se obtienen las demás notas que completan los doce sonidos en los que se pueden separar una octava en una escala cromática.

       En el presente video se aprecian algunos ejemplos de intervalos consonantes y disonantes, clasificados los primeros en perfectos e imperfectos, los segundos en suaves y fuertes. Ambas clasificaciones representan la consonancia o disonancia en mayor y menor medida.

       Los intervalos de consonancia perfecta fueron determinados gracias a los experimentos con el monocordio, más aún, las proporciones en sus longitudes y su fundamentación matemática en la aplicación de la media aritmética, media geométrica y media armónica.

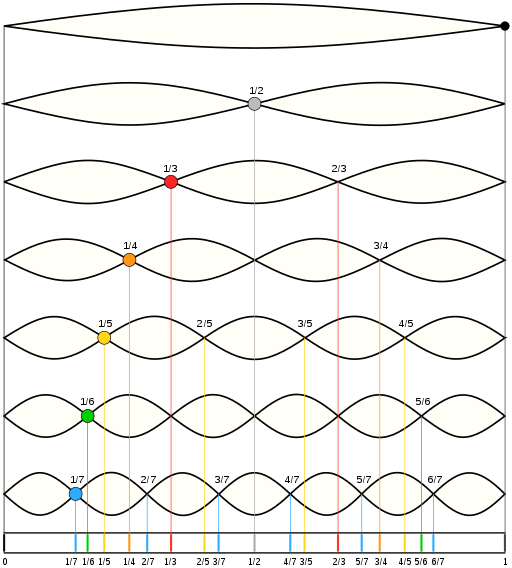
       Variando la longitud de la cuerda vibrante en el monocordio, los pitagóricos pudieron comparar los diferentes sonidos generados y así la consonancia o disonancia entre ellos. Concluyendo que, aquellos que más corresponden a la nota que produce una longitud de cuerda determinada, son los emitidos a 1/2, 2/3 y 3/4 de su longitud. Estos tres fueron llamados respectivamente diapasón, diapente y diatesarón. Actualmente se conocen como intervalo de octava, quinta y cuarta.

Fuente

       Dicha relación entre las longitudes de cuerdas y los sonidos emitidos se mantiene en otros objetos y magnitudes, como el largo de un tubo o tudel en los instrumentos de viento y el volumen de las campanas, además se relata que Pitágoras notó la consonancia y disonancia entre los sonidos que emitían los martillos con sus diferentes masas sobre el yunque de una herrería y de allí se inspiró a realizar los análisis antes mencionados.

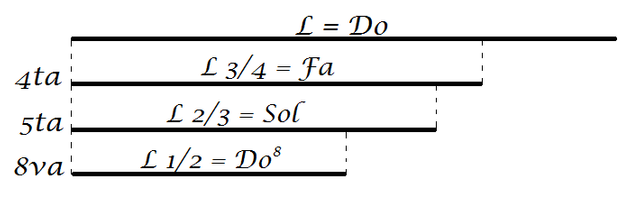
       Lo que la imagen anterior muestra es que si una cuerda de distancia 'L' proporciona un Do por ejemplo, un medio de su distancia producirá un Do pero una octava más agudo, dos tercios de su longitud produciría un Sol que es equivalente a un intervalo de quinta y tres cuartos de la distancia inicial proporciona un Fa que es equivalente a un intervalo de cuarta.

       Los números enteros, en especial los primeros cuatros era muy especiales para los Pitagóricos, el Tetraktys por ejemplo era una figura geométrica que ordenaba cuatro filas de uno, dos, tres y cuatro elementos que en total sumaban diez, representaba para ellos un símbolo místico de mucha importancia.

Fuente

       De tal manera que se hizo igual de relevante el hecho de que los primeros cuatros números enteros bastaran para determinar las proporciones 1/2, 2/3 y 3/4 que determinan los intervalos de mayor consonancia en la octava musical.

       Las relaciones consonantes y su correspondencia con las medias.

       Otro factor que causó impacto es que dichas proporciones son demostrables de forma analítica por la media aritmética, media geométrica y media armónica. Hoy en día conocemos la frecuencia aproximada de la vibración de cada nota musical, mediante estas se puede corroborar dichas proporciones con las medias antes mencionadas.

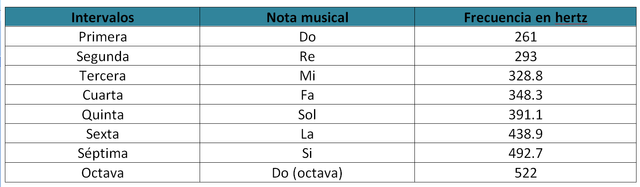
       La media aritmética de una nota y su octava puede determinar el intervalo de quinta, esta se expresa de la siguiente manera:

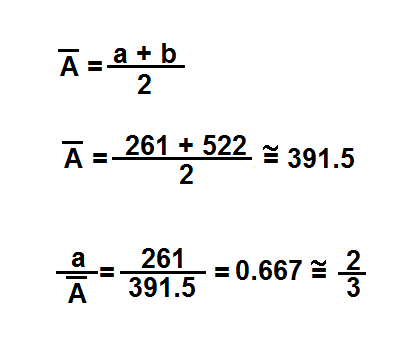
       Sustituyendo 'a' por la frecuencia del Do inferior y 'b' por la de su octava se obtiene un valor muy parecido al de la nota Sol, es decir el intervalo de quinta. De igual manera el cociente entre la frecuencia de una nota (en este caso Do) y su media aritmética representa la relación del intervalo de quinta.

       Como en el caso anterior, la media armónica de la frecuencia de una nota y su octava puede determinar la frecuencia de su cuarta, así como se expresa a continuación:

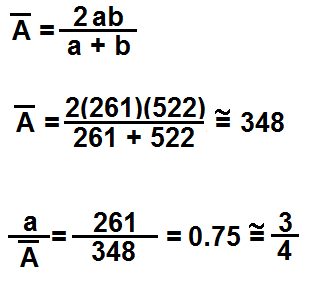
       Sustituyendo 'a' por la frecuencia de Do y a 'b' por la de su octava se obtiene el valor de Fa, es decir la cuarta de Do. De igual manera, el cociente entre Do y el valor de su media armónica representa la relación del intervalo de cuarta.

       La media geométrica es la raíz enésima del producto de n elementos, es decir que aplicado a una nota y su octava, sería la raíz cuadrada del producto entre ambas frecuencias. Pero a su vez esta puede caracterizar la relación entre una octava y otra, de la siguiente manera:

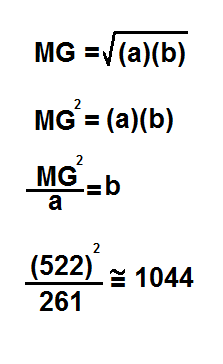
       Sustituyendo 'a' por la frecuencia de Do y 'MG' por la de su octava se obtiene el valor del Do de la octava siguiente. Visto de otra manera:

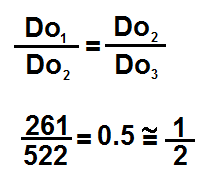
       El cociente entre ambos valores representa la relación del intervalo de octava.

       A partir de las relaciones entre una nota y sus consonantes (cuarta, quinta y octava), los pitagóricos pudieron determinar las proporciones con el resto de las notas que componen una octava musical. En la siguiente entrega se desarrollará más acerca de esto, además se abordará la incompatibilidad que existe entre las quintas y las octavas de una nota y de las complicaciones que esto generó en el sistema de la afinación pitagórica.

Fuente

       Para concluir el presente trabajo se puede mencionar lo poético y maravilloso que pudo haber resultado para los Pitagóricos encontrar tanta armonía (a propósito de música) entre las notas musicales, sus proporciones consonantes, los números enteros y las medias. Todo esto les llevaría a encontrar relaciones incluso con la astronomía, dándole entrada a otras teorías como la de la música de las esferas que bien pudiera tratarse en otro artículo.

       Lecturas Recomendadas:

Pitágoras, las matemáticas y la música

El fundamento matemático de la escala musical y sus raíces pitagóricas

Pitágoras & La música

2,500 años de temperamentos musicales

Semitono y Afinación pitagórica

El sistema pitagórico

Modelos matemáticos del sistema de afinación pitagórico y algunos de sus derivados

---

       Esperando que este artículo haya sido de mucho agrado y provecho para los lectores, me despido cariñosamente desde Apure - Venezuela.

Todas las imágenes expuestas donde no se mencionan las fuentes fueron creadas por @leonardoj333.