¿Por qué se mantienen en equilibrio las bicis en movimiento?
¡Hola Steemers! Con este post quiero demostrarles que la ciencia, además de ser necesaria, también puede llegar a ser interesante y hasta divertida, pero esto dependerá de la actitud de cada quien. Particularmente me encanta buscarle utilidad a todo lo que voy aprendiendo en los libros y en clases, así que hoy voy a hablarles de una de mis cosas favoritas… ¡Bicis!

Dicen que manejar bici es algo que nunca se olvida, ¡¿y cómo podríamos?! Si la bici es un mecanismo tan genial, que tiene sus propios recursos que se activan automáticamente para ayudarnos a mantener el equilibrio. Es decir que, si la bici se inclina hacia un lado, el volante gira automáticamente en esa dirección, y como resultado, la bici se mantiene balanceada. Esto sucede gracias a una serie de factores (entre ellos, el que va montado en la bici) que actúan en conjunto, como la estructura de la bici, a la distribución su peso y a la precesión, que es el tema que voy a abordar a continuación.
La precesión, un fenómeno que pone a prueba el sentido común
Voy a saltarme la definición abstracta de los libros y les mostraré un claro ejemplo de la precesión.

Para esto, voy a tomar la rueda de una bici y la sujetaré con una cuerda atada a su eje de rotación. Si la sostengo verticalmente y luego la suelto, lo lógico es que caiga, volviendo a su posición inicial.
Ahora haré algo similar, pero al colocarla verticalmente, la haré girar y luego la soltaré. ¿El resultado? La rueda se mantiene vertical y girando alrededor del cordón. ¡Así luce la precesión, como magia!

Pero antes de entrar en detalles, repasemos los siguientes conceptos:
-Vectores:
Un vector es simplemente un segmento que dibujamos para representar gráficamente la dirección, sentido y módulo de alguna magnitud física. Cuando hablamos de cantidades vectoriales nos referimos a parámetros que tienen una dirección, un sentido, y desde luego, una magnitud. La aceleración de la gravedad es un ejemplo de vector, su magnitud es aproximadamente 9,8 m/s2 y su dirección y sentido apuntan al centro de la tierra.
-Torque, momento de torsión o simplemente momento:
El torque está relacionado con el giro que es capaz de causar una fuerza. En palabras sencillas, el torque es una cantidad vectorial (porque tiene dirección y sentido) que expresa la facilidad de impartir o alterar la rotación de un cuerpo.
Lo anterior se escribe –matematicamente- así: .gif)

Es lógico pensar entonces que entre mayor sea la fuerza, mayor será el momento, y de igual forma entre mayor sea el brazo, mayor será el momento. Esto explica por qué es más fácil (se necesita menos fuerza) desenroscar una tuerca sujetando la llave por el extremo. (¿Se te ocurre otro ejemplo? Déjamelo en los comentarios)
-Cantidad de movimiento angular:

Ésta cantidad vectorial sirve para expresar de otro modo la rotación de un cuerpo, y se calcula así: 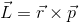
En donde r es el brazo mencionado anteriormente y p es la cantidad de movimiento lineal.
Al igual que el momento, la cantidad de movimiento angular es perpendicular al plano que forman r y p, pero se representa con una línea recta perpendicular a dicho plano de giro.
¡Ahora apliquemos todo esto a la rueda del comienzo!
Si sujetamos la rueda verticalmente y luego la soltamos, ésta cae por su propio peso y ocurren dos cosas: aparece un momento alrededor del eje y que hará que la rueda se balancee de un lado al otro, y además, la cantidad de movimiento angular (que antes era cero) se incrementa (en .gif) ) a medida que la rueda (por acción de su propio peso) tiende a girar en torno a y. Este incremento
) a medida que la rueda (por acción de su propio peso) tiende a girar en torno a y. Este incremento .gif) es perpendicular al plano de giro, así que nos queda lo siguiente:
es perpendicular al plano de giro, así que nos queda lo siguiente:

Pero si antes de soltarla la hacemos girar alrededor del eje x (esto es, alrededor de su eje natural de giro), creamos un momento en dicho eje y por lo tanto, al soltarla, la cantidad de movimiento angular inicial en esa misma dirección no será cero sino L.

Si unimos la información de ambas imágenes, es decir, al considerar el movimiento completo nos queda algo así:

Como tenemos dos componentes para la cantidad de movimiento angular, una sobre el eje x (L) y otra sobre el eje y (dL), la cantidad de movimiento angular total será el vector L+dL
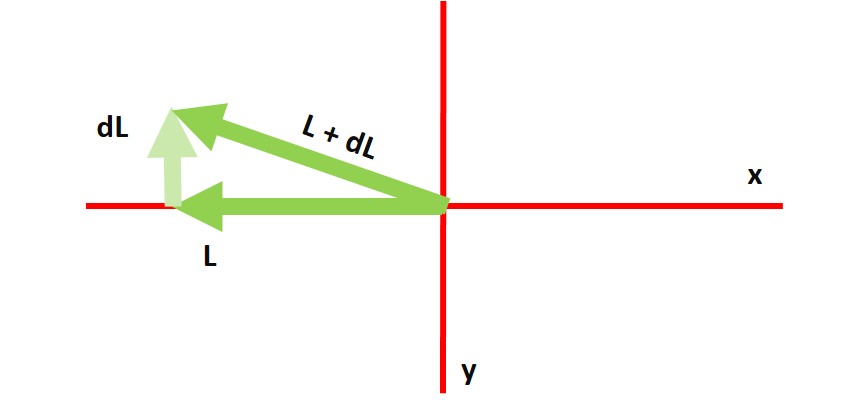
Como se observa en la imagen, la dirección del vector L cambia debido al incremento de dL en un periodo de tiempo dt, y continúa cambiando a medida que transcurren los segundos, hasta que la rueda se detiene debido a la fricción y se acaba la magia. Por esta razón no podemos mantener el equilibrio sobre una bici que no está en movimiento, o al menos no con mucha facilidad.
Así que si no sabes manejar bici aun, no tengas miedo, ¡la física está a tu favor!
Nos leemos en la próxima. Recuerda darle upvote si te gustó y follow para leer contenido similar (:
Aclaratoria: las imagenes son de mi autoría y fueron editadas en Power Point, y las fórmulas las hice gracias a ésta página
Wow, bastante curioso... y me encanta tu post en general, se nota que lo haz trabajado mucho y le haz echado ganas! Sin duda me paso por tu blog!
Gracias! Es halagador.
A mi me encanta la fotografía así que seguro me verás por tu blog también, un saludo (;
No me había hecho esa pregunta nunca pensaba que era por nuestro peso 😵 muy buen post Bro te quedó genial
Me alegra que haya sido de tu agrado y que te hayas aclarado la idea jaja, un saludo.