Diferencia de Conjuntos
Saludos a todos, el día de hoy seguimos estudiando la temática relativa a las Operaciones con Conjuntos, ya faltando muy poco para concluir y dar inicio a otros saberes matemáticos de interés para la comunidad steemiana. En esta oportunidad abordamos la operación Diferencia de Conjuntos que representa un concepto matemático de gran utilidad en la vida diaria de los seres humanos, aunque muchas veces pueda aplicarse de forma natural sin comprender que se hace alusión al mismo, de allí la importancia de ir explicando en las diferentes publicaciones tanto los aspectos teóricos como sus ámbitos de aplicación y/o utilidad.
En este caso, comencemos analizando desde lo habitual a que se refiere el concepto de diferencia y es que seguramente lo primero que se nos viene a la mente tiene que ver con cualidades, aspectos o características en las cuales no se tiene coincidencia, acuerdo o similitud alguna. Esto nos indica que algo o alguien es diferente a otro porque no hay coincidencia en algunos o todos los detalles que lo integran. En el caso de los conjuntos (que ya sabemos por publicaciones anteriores que identifican porciones de la realidad y cotidianidad del ser humano) se presenta por analogía la misma situación, en tanto que se puede determinar tomando en cuenta los elementos que están en uno pero no en el otro.
Ya refiriéndonos a la definición matemática tendríamos lo siguiente: Sean A y B dos conjuntos cualesquiera subconjuntos del Conjunto Universal, se define su diferencia como el conjuntos formado por todos los elementos del universo tales que éstos pertenecen al primer conjunto pero no pertenecen al segundo conjuntos. Simbólicamente se tiene
De la misma manera en la cual es posible precisar la condición que caracteriza los elementos que pertenecen al conjunto diferencia también es posible identificar la cualidad de no pertenencia, esto es, que un elemento cualquiera no estará en el conjunto A-B si no pertenece al primer conjunto o pertenece al segundo, tal como se muestra algebraicamente en la siguiente imagen
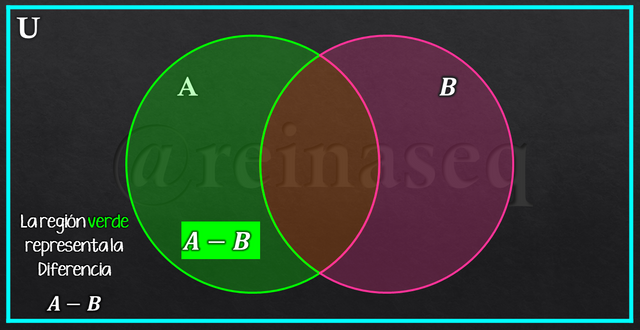
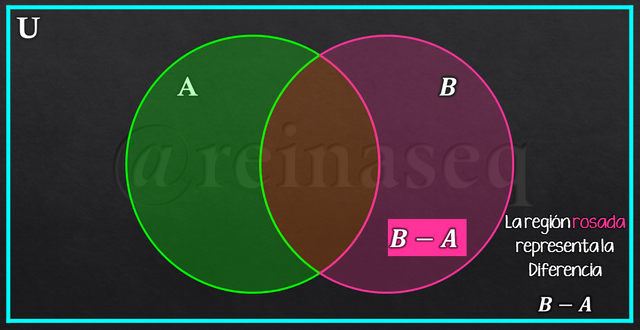
La Diferencia de Conjuntos puede ser representada mediante un Diagrama de Venn tal como se visualiza en las imágenes siguientes
De lo observado, se puede inferir que la Diferencia de Conjuntos no cumple con la propiedad conmutativa, esto es A-B≠B-A.
Antes de estudiar la posibilidad de cumplimiento de otras propiedades habituales en otras operaciones con conjuntos ya analizadas, es importante presentar aquella que puede considerarse la propiedad de mayor importancia, por cuanto que aparte de ampliar las posibilidades de equivalencias con otras operaciones, de igual manera apoya de forma significativa la demostración de teoremas en los cuales en concepto que hoy presentamos estaría involucrado. A continuación se expresará simbólicamente y acto seguido se procederá a la demostración de la misma:
Para la demostración es necesario considerar los siguientes saberes teóricos:
- Definición de Igualdad de Conjuntos (es decir, demostrar la doble inclusión)
- Definición de Diferencia de Conjuntos
- Definición de Complemento de un Conjunto
- Definición de Intersección de Conjuntos
A continuación, desarrollemos la demostración:
i ¿ A-B⊂A∩B'?
∀x∈A-B⇒x∈A∧x∉B , por definición de diferencia de conjuntos
⇒x∈A∧x∈B', por definición de complemento de un conjunto
⇒x∈(A∩B'), por definición de intersección de conjuntos
∴Se demuestra que A-B⊂A∩B', por definición de Inclusión de Conjuntos.
ii ¿ A∩B'⊂A-B?
∀x∈A∩B' ⇒x∈A∧x∈B', por definición de intersección de conjuntos
⇒x∈A∧x∉B, por definición de complemento de un conjunto
⇒x∈A-B , por definición de diferencia de conjuntos
∴Se demuestra que A∩B'⊂A-B, por definición de Inclusión de Conjuntos.
∴ Por i y ii se demuestra que A-B=A∩B', por definición de Igualdad de Conjuntos ∎
Ahora bien, una vez demostrada esta importante propiedad podemos considerar estudiar si es posible el cumplimiento de propiedades que hemos estudiado para otras operaciones. Primeramente comencemos con la Idempotencia, es decir, ¿será posible A-A=A?, bien si nos apoyamos en la propiedad anterior tendríamos el siguiente escenario:
Pero resulta que si analizamos A∩A' nos damos cuenta que estamos en el terreno del complemento de un conjunto y recordamos que no existen elementos en común entre un conjunto y su complemento, por tanto su intersección es vacía. Esto indica que la propiedad de idempotencia no es posible en la operación Diferencia de Conjuntos. En consecuencia, lo que se verifica por el estudio anterior es
En lo que respecta a la posibilidad de verificación de la propiedad asociativa, sería preguntarnos si ¿ (A-B)-C=A-(B-C)? Este cuestionamiento podría ser fácilmente dilucidado si apoyándonos en propiedades de conjuntos vistas previamente (en publicaciones anteriores) desarrollamos por separado ambos miembros de la igualdad. Comencemos:
I) (A-B)-C=(A-B)∩C', por propiedad de diferencia de conjuntos A-B=A∩B'
=(A∩B')∩C', por propiedad de diferencia de conjuntos A-B=A∩B'
Al desarrollar el primer miembro de la igualdad nos damos cuenta que ya llegamos al tope de las posibilidades de manera tal que si se espera que se cumpla esta propiedad la única alternativa sería que al desarrollar el segundo miembro de la igualdad llegáramos exactamente a la misma expresión. Veamos a continuación lo que ocurre:
II) A-(B-C)=A∩(B-C)', por propiedad de diferencia de conjuntos A-B=A∩B'
=A∩(B∩C')', por propiedad de diferencia de conjuntos A-B=A∩B'
=A∩[B'∪(C' )'], por Ley de De Morgan
=A∩(B'∪C), por propiedad involutiva del complemento de un conjunto
Como podemos observar, al desarrollar ambos miembros de la igualdad llegamos a resultados diferentes, razón por la cual se evidencia que en el caso de la operación Diferencia de Conjuntos no se cumple la propiedad asociativa.
Ahora verifiquemos si se cumple la propiedad distributiva, es decir, ¿se cumplirá que A∩(B-C)=(A∩B)-(A∩C)?
Tal como lo hicimos en el caso anterior, desarrollaremos cada miembro de la igualdad haciendo uso de propiedades de las operaciones con conjuntos ya estudiadas, posteriormente comparamos ambos resultados y si éstos coinciden se puede afirmar que si se cumple la propiedad. Procedamos:
I) A∩(B-C)=A∩(B∩C'), por propiedad de diferencia de conjuntos A-B=A∩B'
En este caso, sólo basta con aplicar una propiedad y queda explícitamente desarrollada la expresión. Continuemos con el segundo miembro de la igualdad
II) (A∩B)-(A∩C)=(A∩B)∩(A∩C)', por propiedad de diferencia de conjuntos A-B=A∩B'
=(A∩B)∩(A'∪C'), por Ley de De Morgan
=[(A∩B)∩A']∪[(A∩B)∩C'], por propiedad distributiva de la unión respecto de la intersección de conjuntos
=[A∩(B∩A')]∪[A∩(B∩C')], por propiedad asociativa de la intersección de conjuntos
=[A∩(A'∩B)]∪[A∩(B∩C')], por propiedad conmutativa de la intersección de conjuntos
=[(A∩A')∩B]∪[A∩(B∩C')], por propiedad asociativa de la intersección de conjuntos
=[∅∩B]∪[A∩(B∩C')], por propiedad A∩A'=∅
=∅∪[A∩(B∩C')], por propiedad A∩∅=∅=∅∩A
=A∩(B∩C'), por propiedad A∪∅=A=∅∪A
Como podemos observar, en ambos casos hemos llegado a la misma expresión, esto indica que se cumple la propiedad distributiva A∩(B-C)=(A∩B)-(A∩C) para la Diferencia de Conjuntos.
Es evidente que esta operación se apoya en las propiedades de operaciones ya estudiada, esto es porque su definición guarda cierta relación con el complemento de un conjunto y la intersección de conjuntos. Otra precisión válida de la Diferencia de Conjuntos tiene que ver con el caso de los conjuntos disjuntos, es decir, aquellos cuya intersección es vacía, en tanto que al plantear la diferencia nos encontraremos con lo siguiente:
En este punto, puede causar interés saber cómo aplica el concepto Diferencia de Conjuntos en un caso de la cotidianidad, para lo cual ilustraré con un sencillo ejemplo. Imaginemos dos estudiantes de una carrera de pregrado cualquiera, cada uno con un historial de calificaciones semestral en la asignatura Matemática, específicamente hablando, las calificaciones del primer estudiante forman un conjunto A y las calificaciones del segundo estudiante integran el conjunto B. Como sabemos es posible que entre dos estudiantes cualesquiera existan calificaciones coincidentes, bien sea por la perspectiva evaluativa del profesor o porque se trata de trabajos o producciones grupales en los que ambos reciben la misma calificación. Ahora bien, si quisiéramos saber cuáles son las calificaciones de ambos de forma individual que no coinciden con el otro, tendríamos que determinar A-B (calificaciones del estudiantes 1) y B-A (calificaciones del estudiantes 2). Los conjuntos serían:
A={11,12,14,15,16,17,19}
B={10,12,13,15,17,18,20}
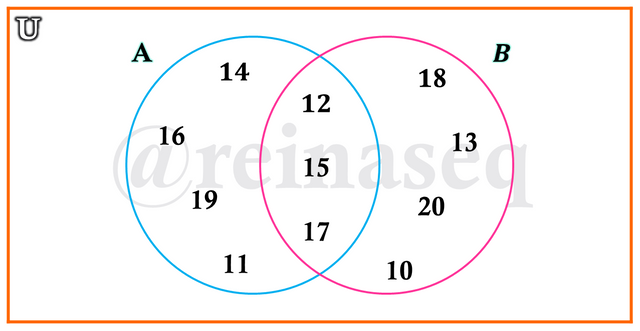
Representando en un Diagrama de Venn tenemos
Para obtener lo solicitado debemos apoyarnos en la definición de Diferencia de Conjuntos, recordamos que un elemento pertenecerá a la diferencia de dos conjuntos si pertenece al primero pero no pertenece al segundo. Esto nos lleva a lo siguiente:
A-B={11,14,17,19} (Calificaciones del estudiantes 1 que no coinciden con el 2)
B-A={10,13,18,20} (Calificaciones del estudiantes 2 que no coinciden con el 1)
Con el ejemplo se logra visualizar que el concepto matemático estudiado es aplicable de forma sencilla en la cotidianidad. Dicho esto, concluyo la temática de hoy, esperando poder leernos en la próxima publicación.

Un matemático que no es en algún sentido un poeta no será nunca un matemático completo - Karl Weierstrass.

Referencia
Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Lipschutz, S. (1970). Teoría de Conjuntos y Temas Afines. Teoría y 530 problemas resueltos. Serie de compendios SCHAUM. Mc Graw-Hill.
Todas las imágenes, separadores y banners de este artículo son de autoría propia.
Artículo Anterior




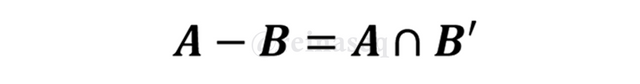
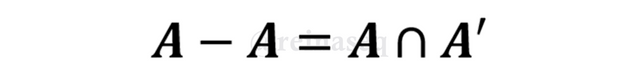
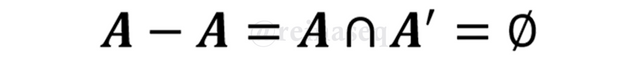

saludos, muy interesante tu post.
Gracias, saludos!!
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by reinaseq from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Que bellos, gracias por la visita, siempre bienvenidos!! Abrazos fraternos!! 🙌✊🎉
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Agradecida por su valoración a mi aporte, saludos y abrazos fraternos a este gran equipo!! 🎓🙌✊🎉🎉🎉
Votado por el trail Team-México @team-mexico
Canal Discord ¡Te esperamos!
Muchas gracias por el apoyo, siempre atentos a la valoración de la comunidad!! Abrazos y saludos cordiales!!
Hi @reinaseq!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Muy agradecida por el apoyo, ya los apoyo como testigo!! abrazos fraternos por su incansable tarea!!
Excelente trabajo @reinaseq. Gracias por compartirlo. Si tienes algún tiempo disponible, te invito a ver mi post sobre la Energía. Saludos.
Muchas gracias por su valoración, aprecio su comentario!! Revisé su trabajo, es un valioso aporte en tiempos de desarrollo sostenible , lo felicito!! Saludos cordiales!!
Resteemed your article. This article was resteemed because you are part of the New Steemians project. You can learn more about it here: https://steemit.com/introduceyourself/@gaman/new-steemians-project-launch