Deducción de la identidad de Euler: La más bella y elegante ecuación de las matemáticas
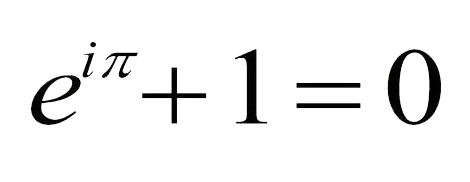
Identidad de Euler

Leonard Euler (1707-1783)
Su manera original y elegante de notación matemática ha trascendido hasta nuestros días, ha sido quien más ha influido en el análisis matemático con su acuciosidad, organización, sistematización y elegancia, al presentar aspectos complejos de la matemática, de la manera más simple y precisa.
La llamada "Identidad de Euler", es un caso especial y particular de una fórmula desarrollada por Euler a partir de series de potencias, que no son más que la representación de funciones a partir de sumas infinitas de términos, a la cuales siempre dispensó una particular atención. Su identidad es un poema matemático sencillo, pues posee 5 números emblemáticos en la historia de las matemáticas:
(número de Euler): Un número trascendente que aparece en muchos fenómenos naturales
(número pi): Un número trascendente que relaciona la longitud de la circunferencia con su diámetro
(número i): Unidad imaginaria, cuyo valor es la raíz cuadrada de -1, y constituye la base de los números complejos
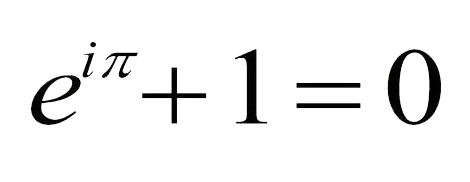 [Identidad de Euler](http://instintologico.com/un-pequeno-homenaje-a-euler/)
[Identidad de Euler](http://instintologico.com/un-pequeno-homenaje-a-euler/)
Euler hizo la deducción de la fórmula que aparece a la derecha, empleando series de potencias a las que era gran aficionado, sin embargo yo particularmente haré primeramente una deducción un tanto más sencilla y fácil de recordar, para luego proceder a hacer de la manera más breve y simple posible la relativamente larga deducción que hizo este gran genio matemático de todos los tiempos.
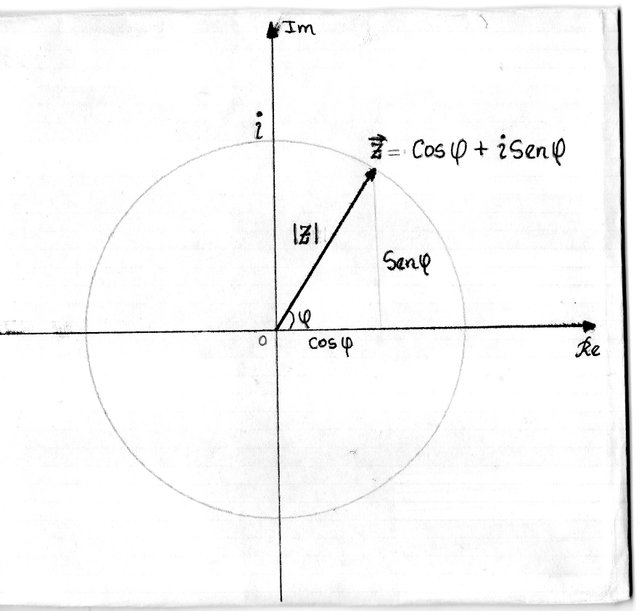
A la derecha observamos el "Plano Complejo". De manera que el vector
suponiendo el módulo nos queda
Luego derivo el vector Z respecto al ángulo (lo que representa la velocidad de giro del vector, cuando barre el área circular)
por tanto la ecuación (a) será:
¡ATENCIÓN! Ahora la genialidad consiste en darse cuenta que:
Sacando factor común i quedará:
ahora podemos observar que lo que está entre paréntesis es:
Ordenando variables a ambos términos de la ecuación:
Aplicando la integral a ambos miembros de la ecuación:
Lo que da como resultado al resolver la integral indefinida:
Esta es la ecuación de Euler en términos generales:
Ahora para el caso particular de
quedaría al sustituir:
y sabiendo que:
Así se vería la ecuación particular.
¡Y de acá!

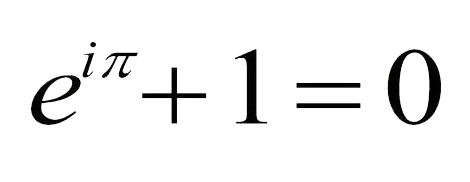
Identidad de Euler
#LeonhardEuler #IdentidadDeEuler #Matematica #AnalisisMatematico #AnalisisNumero #Math #Number #Equation #Mathematicians #GreatMinds #NumericalAnalysis
Derechos de Autor @Sergioddy5 Todos los Derechos Reservados

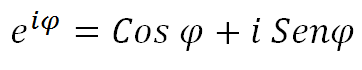
Congratulations @sergioddy5! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - The semi-finals are coming. Be ready!
Participate in the SteemitBoard World Cup Contest!
Collect World Cup badges and win free SBD
Support the Gold Sponsors of the contest: @good-karma and @lukestokes
I want to thank the steemit platform for the follow-up, I have written relatively little in 3 months, I have many interesting things to tell, but I have not had enough time. Soon my number of publications will increase over time.