Y tu ¿Podrás resolver el problema de los puentes de Königsberg? 2º Parte
Hola steemians, como lo prometido hoy les traigo la continuación de mi anterior post (si todavía no lo viste te lo dejo aquí), en donde comente el primer problema que resolví de la rama de la matemática llamada Teoría de Grafos. Básicamente un grafo es un conjunto de objetos llamados vértices unidos por caminos llamados aristas, que te permiten representar y estudiar relaciones binarias entre elementos de algún conjunto y cómo interactúan entre sí. Esto es muy utilizado en ciencias de la computación, por ejemplo: en una red de computadoras o como veremos en el siguiente caso.
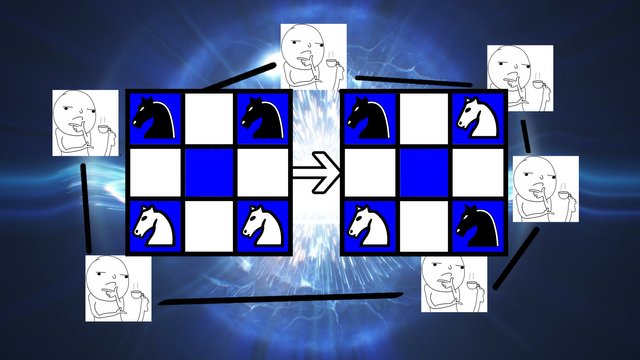

El anterior problema decía lo siguiente:


Respuesta
No es posible, y la manera de demostrarlo es la siguiente:

Primero enumeramos las casillas del tablero 3x3
Luego de eso vemos cada movimiento válido de un caballo dependiendo de la casilla en donde esta, a la que va a ir (ejemplo: 1 -> 6;8 es decir que de la casilla 1 puede irse al 6 o al 8).
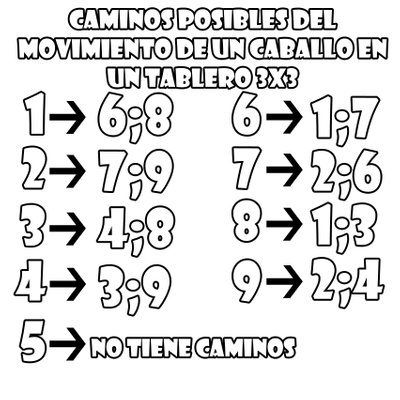
Luego de saber cada movimiento que se puede hacer, esto mismo tiene una restricciòn la cual sigue, lo que significa que hay un camino por donde cada caballo debe de pasar para llegar a una casilla determinada, ahora es el momento de graficar un grafo y quedaría de la siguiente manera:
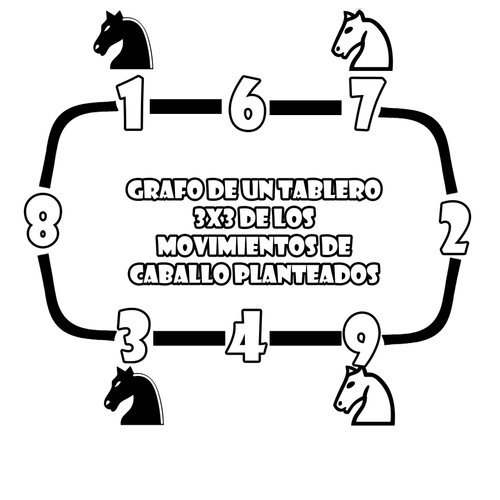
Con este gráfico podemos notar que los caballos blancos siempre iran juntos y los negros de igual manera, es decir, un caballo blanco no puede saltar por arriba de uno negro y para conseguir la segunda configuración el caballo negro debe de estar en el 9 y el blanco en el 3 (imposible) de esta manera se ve que es imposible que llegar a la segunda configuración.

Este fue el método el cual yo utilicé a la hora de resolver el problema, y a usted ¿Se le ocurre otra manera de demostrarlo?
Eso fue todo por este post, no se olviden de votar, comentar y compartirlo!

Usted ha recibido un upvote por la comunidad @inteligentzia y su TRAIL de curadores ya que consideramos su post de información útil y de relevancia creativa.
Si quieres saber más del proyecto aquí te dejamos nuestro post introductorio
También puedes unirte a nuestro canales en el Chat Discord o en nuestro Grupo de Facebook para saber más del proyecto!
Mi voto y el de mi Trail es solo para los usuarios que cuentan con una membresía. Activa la tuya en nuestro DISCORD.