El Dilema de la Secretaria
¿Qué es un dilema? Tal y como comenté en otro artículo recientemente publicado, podemos decir que se trata de una situación que se nos presenta y en la que tenemos que tomar la decisión de elegir entre diferentes opciones o alternativas.
En nuestra vida nos encontramos constantemente con dilemas que tenemos que resolver; por ejemplo una situación típica se da cuando tenemos que salir a la calle y vemos que el tiempo amenaza tormenta. ¿Qué hacemos entonces? Tenemos dos alternativas: llevarnos el paraguas o no llevarlo; si nos lo llevamos y llueve perfecto, pero ¿y si no llueve? ¿y si dentro de un rato sale el sol? En este caso el paraguas puede resultar una molestia e incluso es fácil que nos lo dejemos olvidado en algún lugar.
Lo que he planteado parece una tontería pero sirve como ejemplo para ilustrar situaciones típicas que a diario se nos plantean y que nos obligan a elegir entre diferentes alternativas.
La cosa se complica cuando las situaciones que nos encontramos, y que suponen un dilema, son importantes para nuestra vida. Evidentemente no es lo mismo el dilema que supone elegir si nos llevamos o no el paraguas, al dilema que supone elegir entre dos puestos de trabajo, o todavía más allá, el dilema de elegir pareja.

En muchos casos la elección debe producirse entre solo dos alternativas, así que la probabilidad de elegir la mejor opción siempre va a estar en un 50%. ¿Pero qué sucede si tenemos que elegir entre más de dos alternativas? Aquí la cosa se complica ya que en teoría, a mayor número de alternativas para elegir, menor probabilidad de acertar con la mejor opción.
Pongamos un ejemplo con el que se suele ilustrar este caso: tenemos 3 sobres con dinero de tal manera que cada sobre tiene una cantidad diferente de dinero; tenemos la opción de abrir un sobre al azar y decidir si nos quedamos con lo que hay en su interior, o desecharlo y abrir el siguiente; cada vez que desechemos un sobre ya no lo podemos recuperar. ¿Existe alguna manera de maximizar la mejor elección? Habrá gente que por temor, elegirá la primera opción y se conformará con ella; por el contrario otras personas esperaran a abrir el último sobre pensando que la última opción va a ser la mejor.
En matemáticas existe una teoría llamada “el problema de la parada óptima” que sirve para definir qué momento es el mejor para detenerse y maximizar la probabilidad de tener éxito. ¿Supone esto tener siempre el mejor resultado? Evidentemente no, e incluso podemos llegar a elegir la peor opción de todas, pero de lo que se trata es de tomar la decisión más inteligente que nos permita una mayor probabilidad de obtener la mejor decisión; es lo que en economía se denomina “maximizar las recompensas y minimizar los costes”.
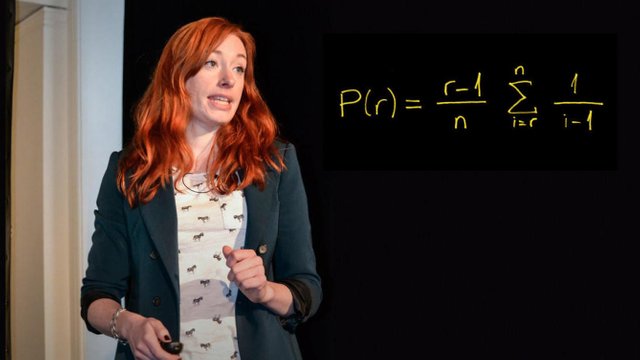
Volviendo al tema de los sobres de dinero, si escogemos uno de ellos al azar tendremos un 33,3% de probabilidades de conseguir la mejor opción. Ahora bien, si partimos del hecho que existe un total de 6 posibles combinaciones entre los 3 sobres, el problema de la parada óptima nos dice que para maximizar las probabilidades de éxito debemos rechazar el primer sobre, tenga la cantidad de dinero que sea, y elegir el siguiente sobre que tenga una cantidad mayor. De esta forma en 3 de las 6 ocasiones obtendremos la mejor opción, con lo cual nuestra probabilidad sube al 50%.
A partir de la teoría del problema de la parada óptima surge el llamado dilema de la secretaria, que plantea una situación en la que un empresario tiene que elegir a su nueva secretaria, y para ello entrevista varias candidatas.
El empresario comenzará a recibir a cada una de forma individual, y tras acabar la entrevista deberá decidir si se queda con ella o la desecha y continúa recibiendo nuevas candidatas. En caso de desecharla ya no podrá volver a llamarla. Hay que tener en cuenta que hay que optimizar el tiempo, y las empresas tienen que tomar decisiones rápidas y eficientes, con lo cual no es práctico entrevistar a todas las secretarias para posteriormente tomar una decisión. Al igual que con el caso de los sobres de dinero, si tenemos tres secretarias entre las que poder elegir, podemos optar por elegir una al azar o bien emplear una estrategia adecuada.

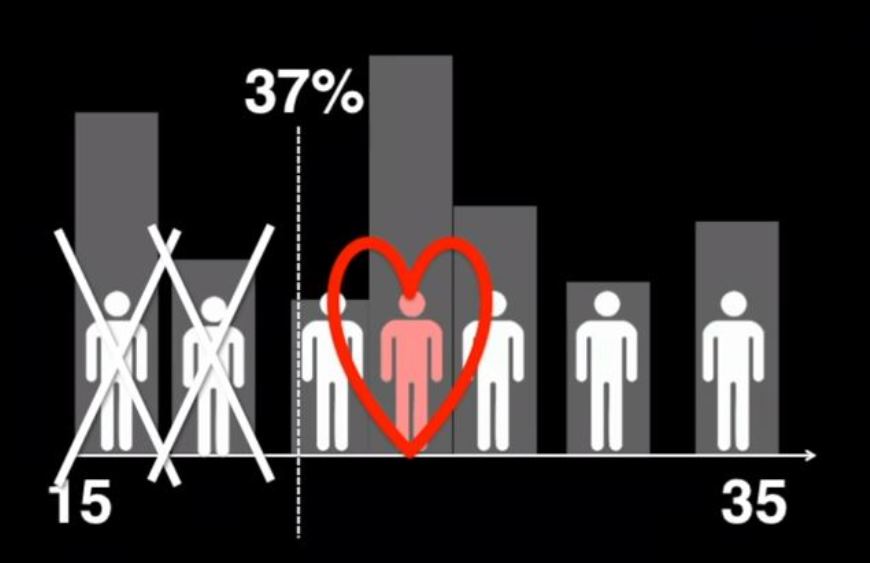
De acuerdo con el problema de la parada óptima, el empresario debe valorar con una puntuación a la primera secretaria, y a continuación rechazarla. A partir de ahí deberá quedarse con la primera candidata que supere esa puntuación, aunque sospeche que la posterior pudiera ser mejor. De esta manera conseguirá aumentar al 50% la probabilidad de escoger la mejor opción ya que en 3 de los 6 casos posibles obtendrá éxito.
En función del número de secretarias que haya para elegir, deberemos optimizar esta táctica; para ello existe una fórmula matemática según la cual habrá que desechar determinado número de candidatas antes de quedarse con la que puntúe más alto que la más alta de las desechadas.
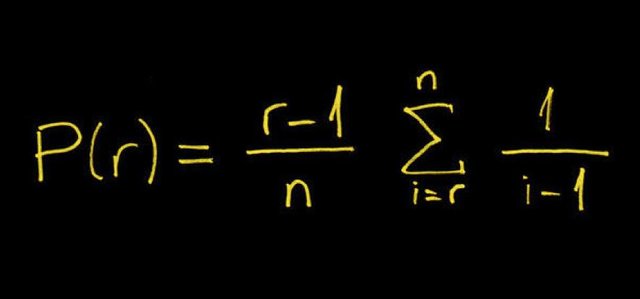
Esta fórmula matemática es un tanto compleja pero se puede resumir diciendo, de forma aproximada, que el número de opciones desechadas debe ser igual al número de opciones dividido por una constante equivalente a 2,71 (a esta constante se la llama número de Euler)
N=M/e
Pongamos un ejemplo; si tenemos 10 sobres con dinero, deberemos desechar los 4 primeros y escoger el primero que sea más alto que el que tenía más dinero de los 4 (N=10/2,71= 3,69)
De igual manera si tenemos que entrevistar a 20 secretarias, y poco tiempo para hacerlo y tomar una decisión, deberemos aplicar dicha fórmula, de tal forma que deberemos desechar a las 7 primeras (N=20/2,71=7,4)
Hay que decir que el dilema de la secretaria y la teoría del problema de la parada óptima son muy utilizados en economía empresarial a la hora de maximizar beneficios, y también es muy utilizada por las empresas a la hora de seleccionar personal.
A modo de curiosidad también se plantea como ejemplo a la hora de elegir pareja; ¿cuántos pretendientes deberemos rechazar en nuestra vida antes de encontrar a nuestra media naranja?


Fuentes:
https://elpais.com/elpais/2017/10/05/ciencia/1507193569_927193.html
https://robologs.net/2018/02/14/el-dilema-de-la-secretaria-o-como-elegir-pareja-con-la-ayuda-de-las-matematicas/
https://blogs.20minutos.es/mati-una-profesora-muy-particular/tag/problema-de-la-secretaria/
http://www.elmundo.es/ciencia/2015/02/14/54df6af6268e3ea3678b4573.html
http://www.disfrutalasmatematicas.com/numeros/e-euler-numero.html

La estadistica y la probabilidad son muy bonitas pero demasiados exactas y predecibles como para aplicarlas a la vida real. Es mi opinión.
No te creas. Tiene mucha utilidad si se sabe aplicar y se combina con la intuición.
Saludos
Interesante. Pero me quedo una duda, que tal si en la primera vez encuentras el valor mas alto? Ya no podrías escoger. Saludos
No puedes saber que ese es el valor más alto. Puedes pensar que es un valor alto pero no puedes saber si posteriormente va a haber otro superior.
Saludos
Excelente para las personas indecisas o que que se le pasan contemplando muchas opciones, y con el ejemplo de los sobres de dinero pues que mas da engañarse usando probabilidades a no poder conocer cual tiene mas dinero. Ojala y hagas una publicación hablando del tema de a cuántas parejas tendremos que rechazara antes de empatar con nuestra media naranja. Saludos.
Uy, eso es complicado. Depende del éxito que tengas con las chicas. Si eres un ligón empedernido y tienes facilidad para relacionarte supongo que podrías extrapolar a un número imaginario y hacer entonces el cálculo. Si es tu caso te recomiendo profundizar en el tema y obtener más datos.
Realmente lo de los sobres y las parejas eran ejemplos que en si mismo no tienen mucha utilidad, pero sirven para comprender el tema.
Donde realmente si se aplica esto es sobre todo en selección de personal. Grandes empresas donde un día tienen que entrevistar 50 candidatos para un solo puesto; la decisión tiene que ser rápida y lo más efectiva posible.
Saludos
interesante amigo siempre las matemàticas al rescate de la falta de informaciòn y la complejidad. Gracias @torkot de nuevo ahora desde ECUADOR.
Gracias a ti viajero. Espero que todo siga bien.
Saludos
Vaya dilema. A veces infravaloramos nuestra capacidad de decisión y esto es un tema tan importante porque en la mayoría de los casos de allí viene el exito. No importa cuan inteligente o talentoso puedas ser, si estás hecho un rollo con tus decisiones y las tomas siempre mal, tu vida será un desastre. Me imagino @torkot que muchos psicólogos ayudarán en ese aspecto a sus pacientes o ¿no?
Excelente post como siempre. Saludos
La psicología sigue estando muy infravalorada; todavía sigue existiendo mucha gente que piensa que solo sirve para tratar depresiones o problemas adaptativos graves, pero no es así. La psicología es muy útil como apoyo orientacional y motivacional para gente muy normal. En otros países es habitual acudir al psicólogo como algo rutinario, igual que pueda ser acudir a un fisioterapeuta.
Saludos
Con razon aun no tengo pareja estable jajajaja, vale este dilema esta enlazado a Teoria de Juegos es muy interesante aunque siempre existen margenes de error altos... Saludos amigo @torkot
Este Post ha sido Votado por el Trail amigos de @sethroot
Si claro. No está planteada como una teoría infalible sino como una teoría que maximiza probabilidades.
Ánimo que te queda poco para conseguir la definitiva.
Saludos
Jajaja si bueno aqui en Peru tendre que buscar una Venezolana jajaja, bueno quien sabe, por otro lado me estoy animando a usar este dilema y el dilema de los maletines de la teoria de juegos, voy a crear un cursito python y usare este tipo de juegos divertidos para aprender :D
Gracias leerte siempre me renueva los animos y me hace pensar en nuevos temas, aunque ando mal vote 70 soles :S
Me agradó tu artículo. Me gusta que implementen conceptos técnicos para contar una historia. Creo que lo subjetivo no puede ser evaluado en parámetros objetivos. Aplico la probabilidad a eventos, no a personas. Saludos.
De acuerdo pero a menudo lo objetivo y lo subjetivo van de la mano y se complementan.
Muchas gracias!
Eso no se pone a discusión. Espero leerte pronto. Por nada y saludos.
Tiempo sin leerlo mi amigo, espero seguir viendo mas publicaciones suyas, saludos.
Un placer tenerte otra vez por aquí.
Saludos!
Hola amigo la controversia de un dilema es formada por dos conceptos distintos el cual está es formada por una situación en duda " la secretaria tendrá mala fama y porque"
Gracias por el aporte.
Saludos