"SLC-S22W1/Variables and Expressions"

Designer by Pixellap
Hello fellow steemians,today I'll be participating on SLC S22W1//Variables and Expressions by @khursheedanwar.
According to @khursheedanwar variable is a symbol which is used for representation of a value which can alter, modified or changed ,variables are presented by using any alphabetical letters like x, y or z.
Then expression is a group of variables, constants and mathematical operations which combine together. expressions can be represented by including variables, constants and mathematical operations.
E.g
y3+7
In this case
"y" is a variable because it can change at anytime
"3,7" are constant because they can't be change
"+" Is a mathematical symbols
TASK 1 |
|---|
In today's lecture we learnt about dependent and independent variables, and they are different types of variables based on the branch and aspect you want to talk about, so I'll be pointing out continuous and controlled variables .
- Continuous variable: This is a type of variables that can take on an infinite number of value within a give range. Continuous variable can assume any value within an interval ,which means that there are no gaps or jumps between possible values.
For e.g within 1 ,2, 3 ,there are infinite number that you will count after 1 before counting 2 and to 3
E.g 1.111,1.9,2.45,2.86,2.9 and then 3
- Controlled variables: controlled variables is a mathematical variables which is used in experiments or study in other courses. It's a variable that values are kept constant and unchanging to ensure it doesn't affect it outcome . They controlled variables is also known as constant variables in most cases.
E.g
This is example of controlled variables in quadratic equation
y=ax²+bx=c
EXPRESSION |
|---|
- Rational Expression: A rational expression is a fraction in which the numerator and/or denominator are polynomials. It is similar to a rational number (a fraction of integers), but instead of integers, it involves polynomials.
e.g of rational expression are
3x+4x
|
|
e.g of a rational expression |
- Trigonometric Expression:Trigonometric Expression is a mathematical expression that are often used to describe relationships between angles and sides in a triangle. In Trigonometric Expression we can use formula like Pythagoras theorem to solve problems
The Pythagoras Theorem is a fundamental principle in geometry that applies to right-angled triangles. It comes in relationship between the lengths of the three sides of the triangle.
Formula for Pythagoras theorem
c²=a²+b²
c=the hypotenus of the right angle
a and b=the other two side
In solving trigonometric problems we can also use they SOHCAHTOA protocol to solve problems on right angle triangle. SOHCAHTOA is an abbreviated word used to remember the three basic trigonometric ratios for a right-angled triangle: Sine, Cosine, and Tangent.
Stating that
SOH
sin=opposite/hypotenuseCAH
cos=adjacent/hypotenuseTOA
tan=opposite/adjacent
TASK 2 |
|---|
Solving an algebraic expression it's something that one need to be very careful and concentrate on following a guided process or procedure to derive at he or her answer. In my primary school days I was taught on how to use the BODMAS protocol which can be applied in solving an algebraic expression .
So the law states that :
- B-BRACKET:whenever you see any bracket in an equation the first thing you need to do is to open the bracket, but how ?. you need to solve anything that's inside the bracket by doing this you've opened the bracket
e.g (2×4)-3+3
So the first thing we need to do is to solve what's inside the bracket by multiplying 2 by 4 , which is 8 , then our bracket will automatically be open
Our equation will now be written as 8-3+3
And also take note there's a situation whereby there's figure standing beside the bracket for e.g 4(5-2x), how do we open the bracket? Take note in any equation that a figure stand close to a bracket with a mathematical sign ,it simply means that there's an invincible multiplication sign there
You'll just need to multiply 4 by 5 which will give us 20
So our bracket is open to 20-2x
- O-Order: the next steps here is order ,the order simply means power that's usually found in an equation especially the square,cubes . So the law states that solve any power or roots
For e.g 2²+³3³
So you'll need to get rid of the squares and cubes
4+9
- D-Division: After you're done with orders the next rules is division, so division here have to do with division of numbers , and it's just so easy
For e.g
(4-2)+4²÷4
So first we'll open our bracket 4-2=2
So 2+4²÷4
Then we'll then looking into order which is 4²=16
2+16÷4
And now we'll then divide 16 by 4 =4
So our equation will be now be written as 2+4
- M-Multiplication: After the division rules its over to multiplication rules , so in an equation after the division solved , you'll also need to multiply any figure with multiplication sign
For instance 6÷3×4
You'll first divide 6 by 3 =2
2×4
And now we'll be multiplying 2 by 4 =8
- A-Addition: Addition is the addition of numbers, so in an equation after you're done with the multiplication you'll also need to add any figure with addition sign
For e.g 2×4÷2+8
So we'll divide 4 by 2 =2
2×2+8
And now it's multiplication, 2×2=4
4+8 =12
So 12 is our ans
- S-Substraction:after the addition it's substraction,so the same process will be used in substraction also
2×2-12÷6
Firstly we divide 12 by 6 =2
2×2-2
Then we'll multiply 2 by 2 = 4
And now it's substraction 4-2=2
4-2
TASK 3 |
|---|
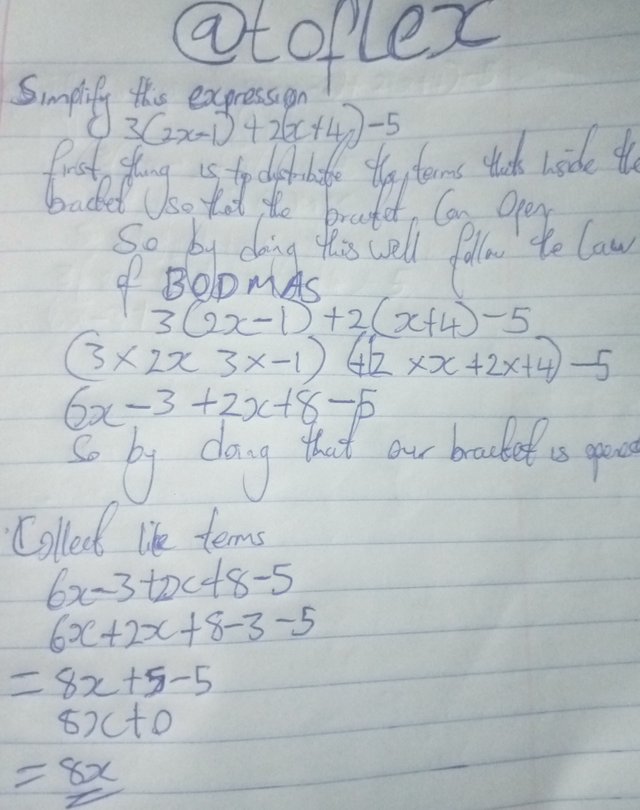
I started by expressing the expression
3(2x-1)+2(x+4)-5
Then after I was done I applied BODMAS to get rid of the brackets
3(2x-1)+2(x+4)-5
So at this point you'll distribute all what that's inside the bracket
(3×2x,3×-1) (+2×x,+2×4)-5
So by doing you've distribute what's inside the bracket and our bracket is open
So our expression will now be written as
6x-3+2x+8-5
Then we'll be collecting like terms
6x+2x+8-5-3
8x+0
=8x

Given that
(x²+2x-3)/(X+1) When x=2
I firstly o substituted 2 to be x
(2²+2(2)-3)/(2+1
Then solved the numerator
(2²+2(2)-3)
The square of 2=4 and I multiplied 2 by what's inside the bracket
4+4-3
=5
Then I calculated the denominator
So our denominator is (2+1)
Which is equals to 3
So therefore
(2²+2(2)-3)/(2+1)
=5/3
And that's our final answer
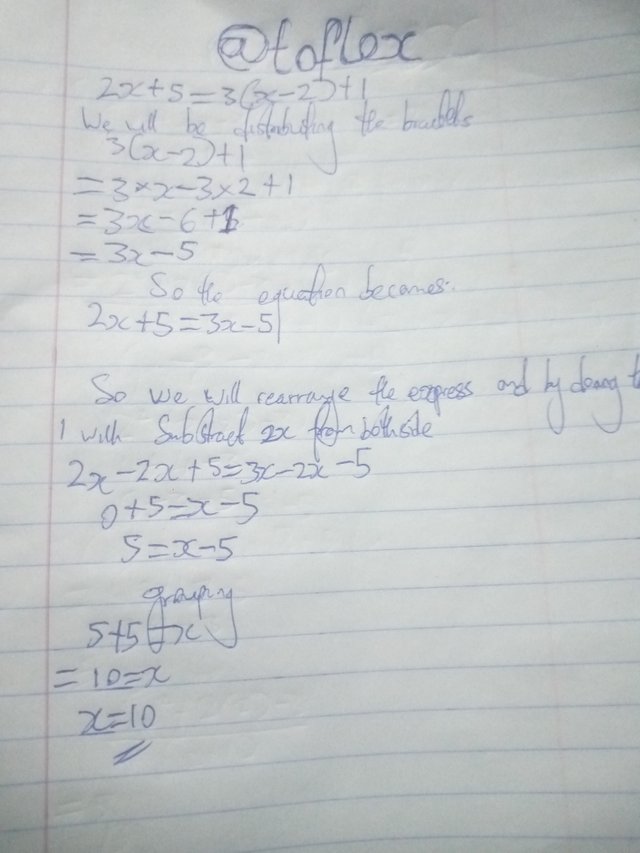
Given that
2x + 5 = 3(x - 2) + 1
I started by opening the bracket at the right hand
(3×x,3×-2)
3x-6+1=3x-5
So the equation will now be
2x+5=3x-5
Then I subtracted 2x from both side
5=x-5
Grouping
5+5=x
X=10
TASK 4 |
|---|
SCENARIO 1
a. Suppose there's a bakery selling a total of 250 loaves of bread per day. They are selling whole wheat and white bread loaves with numbers of whole wheat loaves sold being 30 more than the number of white bread loaves. If x is representing number of white bread loaves sold out and bakery is making a profit of $0.50 for each white bread loaf and $0.75 for each whole wheat loaf then please write an expression for representing bakery total daily profit
SOLUTION |
|---|
To write an expression representing the bakery's total daily profit, I'll be breaking down the information given:
Let's say "x" is the number of white bread loaves sold.
White bread=x
since the number of whole wheat loaves sold is 30 more than the number of white bread loaves, then the number of whole wheat loaves sold can be expressed as X + 30.
Wheat loaves =X+30
the total number of loaves sold is 250. Therefore, we can write the equation as;
X(white loaves)+(x+30) (whole wheat)=250
Now we can it in equation as
x+x+30=250
2x+30=250
2x=250-30
2x=220
We'll divide both side by coefficient of x
X=110
Therefore, the total number of white bread loaves sold is 110. Since;
White bread = X, and X = 110
White loaves = 110
Then, substituting 110 into the equation, Wheat loaves = X + 30, we can then find the number of whole wheat loaves sold has;
Wheat loaves = X + 30, where X = 110,
X + 30 = 110 + 30 = 140.
Therefore, the total number of Wheat bread loaves sold is 140.
Next, we can now calculate the profit:
From the question, the profit from white bread loaves is $0.50 per loaf, so for X white loaves, the profit is 0.50 x X.
And since the profit from whole wheat loaves is $0.75 per loaf, so for (X + 30) whole wheat loaves, the profit is 0.75 x (X + 30).
Now, we can write the expression for the total daily profit as;
Total Profit = Profit from white loaves + Profit from whole wheat loaves
Total Profit = 0.50 x X + 0.75 x (X + 30).
where X = 110
Therefore, substituting x = 110 into the expression gives us;
Total Profit = 0.50 x 110 + 0.75 x (110 + 30)
Total Profit = 0.50 x 110 + 0.75 x 140
Total Profit = 55 + 105
Total Profit = 160.
Therefore, the expression for the bakery's total daily profit is 0.50 x X + 0.75 x (X + 30), and the total profit is $160.
SCENARIO 2
b.Suppose that cost of renting a car for a day is re-presented by the expression 2x + 15 and here x is the number of hours in which car is rented. If the rental company offers a package of 3x - 2 dollars for customers who take car at rent for more than 4 hours then write an expression for the total cost of renting the car for x hours and show how you simplify it.
SOLUTION |
|---|
To write an expression for the total cost of renting the car for x hours, we need to consider two scenarios based on the number of hours rented.
For x hours less than or equal to 4, the cost is given by the expression 2x + 15. i.e., the expression from the question for daily rentage.
Then, for x hours greater than 4, the rental company offers a package deal, which costs 3x - 2.
Now, we can express the total cost based on the value of x:
i.e.,
If x ≤ 4: Total Cost = 2x + 15. and,
If x > 4: Total Cost = 3x - 2.
To simplify the expressions, we'll look at each case:
Case 1: when x ≤ 4
Total Cost = 2x + 15.
This is because the expression 2x + 15 is already simplified.
Case 2: When x > 4
Total Cost = 3x - 2.
This is also because the expression 3x - 2 is also already simplified.
Now, we have two expressions depending on the value of x:
Therefore to rent the car for 4 hours or less, the total cost is 2x + 15.
To rent the car for more than 4 hours, the total cost is 3x - 2.
I'll be inviting @jozzie90,@mirinda1 and @bessie2023 to participate on this SLC
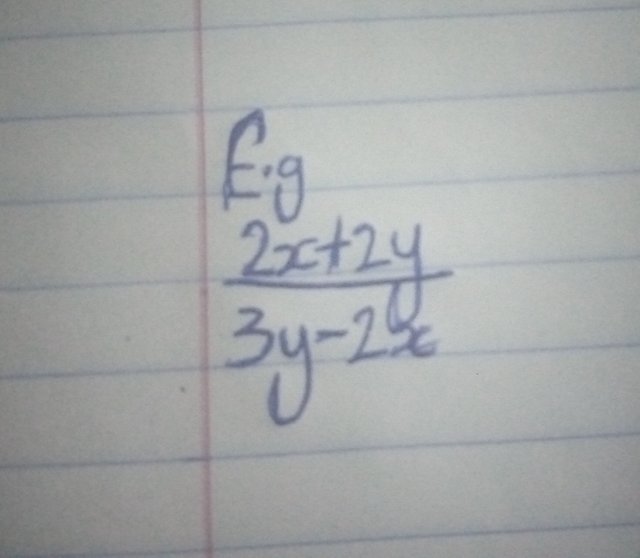
My twitter promotion Link
Nice post my dear friend
Thank you so much dear,I really appreciate the wonderful comments