Mathematics for children (part I): Theory of Mathematics.

gene20 (50)in #steemiteducation • 6 years ago (edited)

In the case of mathematics, mathematics is present in the most diverse situations in our daily life. The meaning of this phrase is great and exhaustive since it affirms that mathematics is present in the most diverse situations in our daily life. This science turns to the study, understanding, and systematization of phenomena modeled by numbers, expressions, algorithms, and geometric shapes. Man, over the years, used Mathematics as a tool to facilitate the organization and structuring of processes, from the banal act of counting sheep in a field to the act of calculating the diameter of the planet Earth.

Mathematics is a science sustained by the correlations we make. An example of this is the decimal numbering system, which was conceived in base 10 because we have 10 fingers on the feet and also on the hands. Mathematics also determines and proves the existence or non-existence of a certain phenomenon or situation. We can cite as an example the criterion of the existence of a triangle, in which the measurements of the sides of that geometric shape cannot occur in a random way.
For a triangle to exist, it must obey the following condition: one of its sides must always be greater than the difference of the other two sides and smaller than the sum of the other two sides.

)
source

In mathematics, for an argument to be true, it must present a mathematical model that guides it. This argument will be defended or answered by means of axioms (absolute truths), theorems, hypotheses, these, and deductions.

There is no exact date for the origin of mathematics because this science has been conceived over many years. Their discoveries were motivated by humanity's needs throughout histories, such as the control of time and the understanding of the cycles of the moon and the frequency of the tides, among many other facts that were vital for the progress of society.

In today's world, understanding mathematics as something implicit or explicit in diverse contexts makes the individual capable of planning and organizing diverse situations.

Mathematics is inserted in the group of exact sciences and has the following objectives:

)
source

Do with what the individual transforms the world around him;

Develop the ability to solve problems;

Stimulate interest and curiosity;

Develop qualitative and quantitative * skills, establishing appropriate relationships;

Identify and organize situations to issue a critical opinion;

Establish mathematical communication through the instruments that science uses.

Mathematics can present divisions and subdivisions in different ways. One of those ways is to divide it into four large groups, which are:

)
source

Space and form: We study geometric shapes and structures by learning how to calculate and size them.

The contents related to space and form are divided as follows:

Location, two-dimensional and three-dimensional figures;

Property of the triangles;

Relations of the quadrilaterals;

Calculation of the area and perimeter of geometric figures;

Identification and operations with angles;

Property of polygons;

Cartesian coordinates;

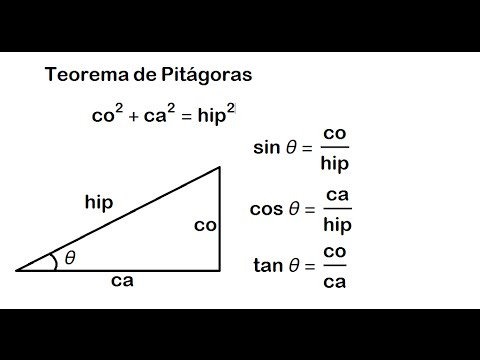
Metric relations of the triangle, the circle and the circumference;

Trigonometric relationships

source

Magnitudes and measures: Used to determine measurement patterns for various types of magnitudes, such as speed, time, capacity, density, volume, among others.