Potential and Kinetic Energy
Potential and Kinetic Energy
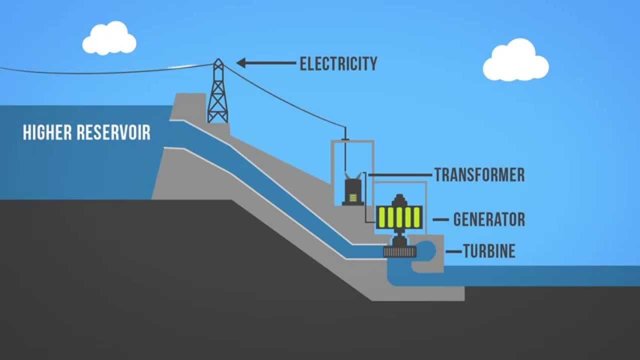
In a hydro-power plant, there is a water reservoir at a certain height. Water flows from pipes and goes into the turbine to rotate it. Through it, we can produce renewable and pollution free electricity which is called hydroelectricity.
When we first know this process, what we are interested in is giving them name and quantifying them. The water reservoir at certain height is causing flow of water which is doing work at the turbine. Energy is the ability to do work and has the SI unit, Joules (J) .The water reservoir at the top and the water flowing through the pipes both have the ability to do work. So, they both possess energy. But, they are in different forms. The water reservoir at the top is static. Let us define this energy as potential energy. If the water reservoir was at a lower level, the ability to do work would be less. Hence, potential energy depends on position. Water flowing in the pipe is in motion. Let us define energy contained as kinetic energy.
Now, we defined what are kinetic energy and potential energy. We will try to quantify them. We already know that energy depends upon the ability to do work. So, there should be a proper notion of work.
The first thing that comes in mind when I listen to the word "work" is a farmer working in a field. But in physics, it is defined differently. The ordinary sense of work doesn't work. If the direction of constant force and displacement are at a certain angle θ with each other, it is given by the product of force along the direction of the displacement and the displacement itself. Force (F) and displacement(S) are vectors. We should be careful about their directions.
Work done = force along direction of displacement × Displacement
= F cos θ × Displacement
= FS cos θ
If direction of force and direction of displacement is same then, cos θ = 1 then,
Work done(W) = FS
Now here are two examples which will convince you that work done in general sense and physical sense are different.
i. Imagine you are holding a box at a certain height. In general sense you are doing work and you will be exhausted after some time. But, the force is due to the weight of the object but there is no displacement of the object in this case. Hence, the physical sense of work done is zero.
ii. Imagine you are holding a box on your back and walking forwards. You are doing work in general sense. The force is due to the weight of object which is vertically downward. You are moving straight so, the force and displacement are perpendicular.
Work done = FS cos(90°) = 0
hence, in physical sense no work is done.
Work done can be defined for more general cases in which force is not constant and displacement is along a curve. In that case, we should use calculus to find the work done. But, to find expressions for kinetic energy and potential energy, we can express it using this simple case.
Potential Energy
Potential energy is the energy possessed by a body by virtue of its shape or position. Consider an object of mass 'm' at ground level. We lift it up to height x above the ground.
Work done = Force × Displacement
Force and displacement are in the same direction.
Force is due to the weight of the object, F = mg
Displacement, S = x
So, work done = FS = mg x
This amount of work done on the object is stored as potential energy in the object. Since the work is done against gravity, the energy is called gravitational potential energy. Potential energy can be elastic potential energy, electrostatic potential energy etc.
It is generally denoted by V and it is function of position; V = V(x).
Kinetic Energy:
Kinetic energy is the energy possessed by a body by the virtue of its motion. Consider an object of mass 'm' initially at rest. We apply force F and displace it by a displacement S with a constant acceleration a in straight line. Let final velocity be v.
Work done = Force × Displacement
According to Newton's second law of motion, F = ma
Displacement, S = s
From law of motion,
v^2 = u^2 + 2as
or, v^2 = 0^2 + 2as
or, v^2 = 2as
or, as = v^2/2
Now,
Work done = F S
= F s
= ma s
= m v^2/2
It is the expression for kinetic energy. Kinetic energy is defined as amount of work done on the object to increase its motion from rest to a given state of motion.
Generally, it is denoted by T.
References




As a science enthusiast, I find this very interesting.
Good job. Keep it up!!
Thank you
Glad you like it