Length of smallest subarray with a sum greater than or equal to S
Problem Statement
Given an array of positive numbers and a positive number ‘S’, find the length of the smallest contiguous subarray whose sum is greater than or equal to ‘S’. Return 0, if no such subarray exists.
Example 1:
Input: [2, 1, 5, 2, 3, 2], S=7Output: 2
Explanation: The smallest subarray with a sum great than or equal to '7' is [5, 2].
Example 2:
Input: [2, 1, 5, 2, 8], S=7Output: 1
Explanation: The smallest subarray with a sum greater than or equal to '7' is [8].
Example 3:
Input: [3, 4, 1, 1, 6], S=8
Output: 3
Explanation: Smallest subarrays with a sum greater than or equal to '8' are [3, 4, 1] or [1, 1, 6].
One simple solution is the brute force solution as seen in the previous blog
but it's not effective, so this problem is another example of sliding window pattern and can be solved using the same approach as before.
Efficient solution:
This problem follows the Sliding Window pattern and we can use a similar strategy as discussed in Maximum Sum Subarray of Size K. There is one difference though: in this problem, the size of the sliding window is not fixed. Here is how we will solve this problem:
- First, we will add-up elements from the beginning of the array until their sum becomes greater than or equal to ‘S’.
- These elements will constitute our sliding window. We are asked to find the smallest such window having a sum greater than or equal to ‘S’. We will remember the length of this window as the smallest window so far.
- After this, we will keep adding one element in the sliding window (i.e. slide the window ahead), in a stepwise fashion.
- In each step, we will also try to shrink the window from the beginning. We will shrink the window until the window’s sum is smaller than ‘S’ again. This is needed as we intend to find the smallest window. This shrinking will also happen in multiple steps; in each step we will do two things:
-
- Check if the current window length is the smallest so far, and if so, remember its length.
- Subtract the first element of the window from the running sum to shrink the sliding window.
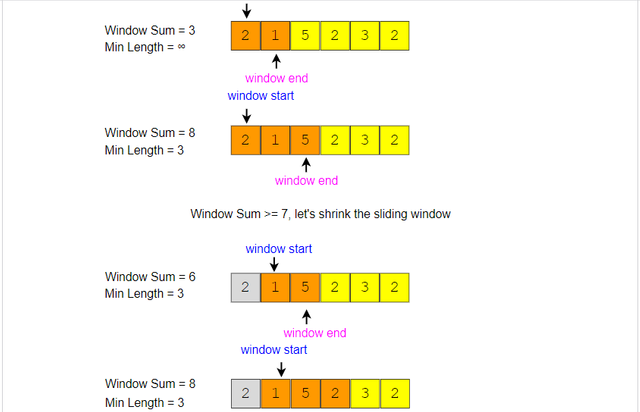
Here is the visual representation of this algorithm for the Example-1

minsum-subarray
Javascript code below:-
<script>
const smallest_subarray_with_given_sum = function(s, arr) {
// TODO: Write your code here
var windowStart = 0;
var minLength = Number.MAX_SAFE_INTEGER;
var windowSum = 0;
for (var windowEnd = 0; windowEnd < arr.length; windowEnd++) {
windowSum += arr[windowEnd];
while (windowSum >= s) {
minLength = Math.min(minLength, windowEnd - windowStart + 1);
windowSum -= arr[windowStart];
windowStart++;
}
}
if (minLength === Number.MAX_SAFE_INTEGER)
return 0;
return minLength;
};
document.write(Smallest subarray length: ${smallest_subarray_with_given_sum(7, [2, 1, 5, 2, 3, 2])}<br/>);
document.write(Smallest subarray length: ${smallest_subarray_with_given_sum(7, [2, 1, 5, 2, 8])}<br/>);
document.write(Smallest subarray length: ${smallest_subarray_with_given_sum(8, [3, 4, 1, 1, 6])}<br/>);
</script>
Time Complexity
The time complexity of the above algorithm will be O(N)O(N). The outer for loop runs for all elements and the inner while loop processes each element only once, therefore the time complexity of the algorithm will be O(N+N) which is asymptotically equivalent to O(N).
Space Complexity
The algorithm runs in constant space O(1).
Posted from my blog with SteemPress : https://www.golibrary.co/length-smallest-subarray-with-a-given-sum/
He said, 'Stop doing wrong things and turn back to God! The kingdom of heaven is almost here.'(Matthew 3:2)
Bro. Eli Challenges Atheism Belief, There is No God
Watch the Video below to know the Answer...
(Sorry for sending this comment. We are not looking for our self profit, our intentions is to preach the words of God in any means possible.)
Comment what you understand of our Youtube Video to receive our full votes. We have 30,000 #SteemPower. It's our little way to Thank you, our beloved friend.
Check our Discord Chat
Join our Official Community: https://steemit.com/created/hive-182074