steempress # 2 "info" APPLICATIONS OF ELASTIC Avior of Arts
APPLICATIONS OF ELASTIC Avior of Arts
The elastic behavior of materials plays an
Important role in everyday life. All engineering
designs require precise knowledge of the elastie
behaviour of materials. For example while
designing a building the structural design of
the columns, beams and supports require
knowledge of the strength of materials used. Have
you ever thought why the beams used in
construction of bridges, as supports etc. have
cross-section of the type Why does a heap of
sand or a hill have a pyramidal shape! Answers
to these questions can be obtained from the
study of structural engineering which is based
on concepts developed here.
Cranes used for lifting and moving heavy loads
from one place to another have a thick metal rope
to which the load is attached. The rope is pulled
up using pulleys and motors. Suppose we want
10 tonnes or metric tons (1 metric ton 1000
to make a crane, which has a lifting capacity of
ko. How thick should the steel rope be? We
obviously want that the load does not deform the
rope permanently. Therefore, the extension
should not exceed the elastic limit. From Table
9.1. we find that mild steel has a yield strength
(S) of about 300 x 10 Nm. Thus, the area of
cross-section (A) of the rope should at least be
A2 W/S, Mg/S, (9.15)
= (10 kg x 10 ms/300 x 108 Nm)
= 3.3 x 10 m
corresponding to a radius of about 1 cm for the rope of circular cross-section. Generally, a large margin of safety (of about a factor of ten in the load) is provided. Thus a thicker rope of radius about 3 cm is recommended. A single wire of the ropes are always made of a number of thin this radius would practically be a rigid rod. So in the manufacture, flexibility, and strength wires braided together, like in pigtails, for ease A bridge has to be designed such that it can withstand the load of the flowing traffic, the force of winds and its own weight. Similarly, in the design of buildings use of beams and columns overcoming the problem of bending of the beam under a load is of prime importance. The beam is very common. In both the cases, the and supported near its ends as shown in consider the case of a beam loaded at the center should not bend too much or break. Let us A bar of length breadth b, and depths when loaded at the center by a load W sags by an amount given by us an
= W 13/(4bd3Y)
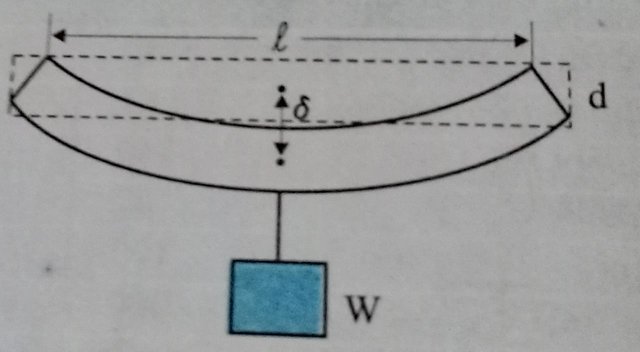
This relation can be derived using what you have already learned and a little calculus. From Eq, we see that to reduce the bending for given load, one should use a material with large Young's modulus Y. For a given material, increasing the depth d rather than the breadth bis more effective in reducing the bending, since is proportional to d-3 and only to b (of course the length l of the span should be as small as possible). But on increasing the depth, unless the load is exactly at the right place (difficult to arrange in a bridge with moving traffic), the deep bar may bend as shown in Fig. This is called buckling. To avoid this, a common compromise is the cross-sectional shape shown in This section provides a large load bearing surface and enough depth to prevent bending. This shape reduces the weight of the reduces the cost. beam without sacrificing the strength and hence
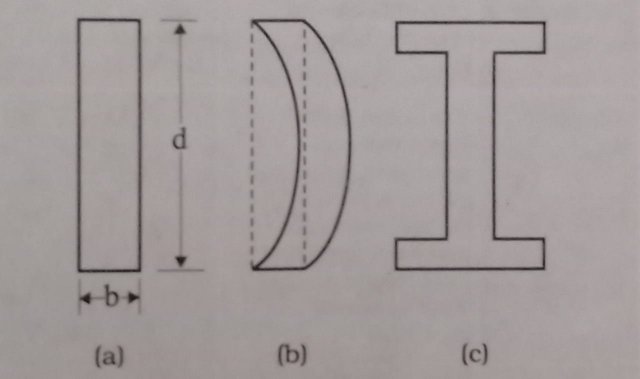
This relation can be derived using what you have already learned and a little calculus. From Eq. we see that to reduce the bending for given load, one should use a material with large Young's modulus Y. For a given material, increasing the depth d rather than the breadth bis more effective in reducing the bending, since S is proportional to d-3 and only to b (of course the length l of the span should be as small as possible). But on increasing the depth, unless the load is exactly at the right place (difficult to arrange in a bridge with moving traffic), the deep bar may bend as shown in Fig. This is called buckling. To avoid this, a common compromise is a cross-sectional shape shown in This section provides a large load bearing surface and enough depth to prevent bending. This shape reduces the weight of then reduces the cost. beam without sacrificing the strength and hence
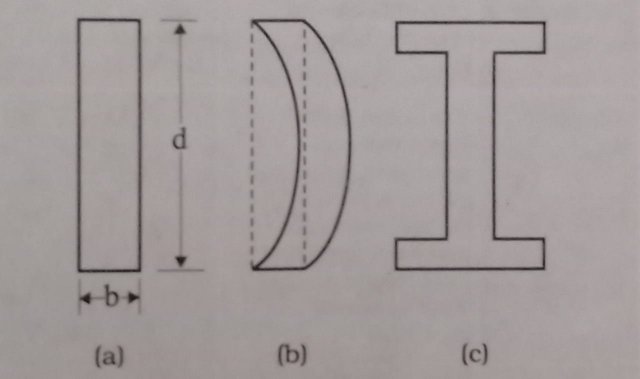
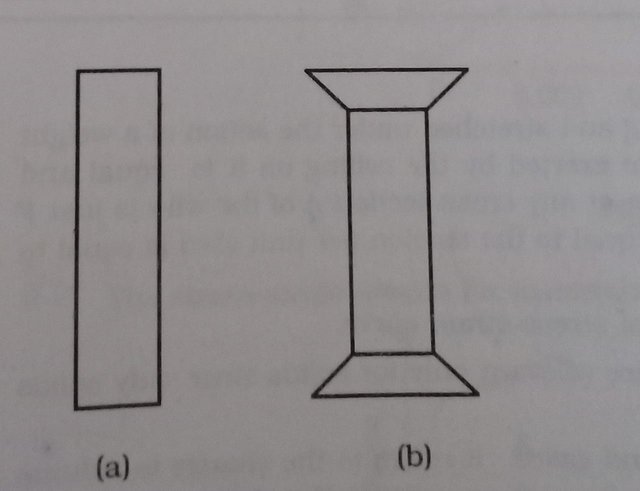
Use of pillars or columns is also very common in buildings and bridges. A pillar with rounded ends as shown in supports less load than that with a distributed shape at the ends The precise design of a bridge or a building has to take into account the conditions under which it will function, the cost and long period, the reliability of usable materials etc.
The answer to the question why the maximum height of a mountain on earth is -10 km can also be provided by considering the elastic properties of rocks. mountain base is not under uniform compression and this provides some shearing stress to the rocks under which they can flow. The stress due to all the material on the top should be less than the critical shearing stress at which the rocks flow.At the bottom of a mountain of height h, the force per unit area due to the weight of the mountain is hpg where p is the density of the material of the mountain and g is the acceleration due to gravity. The material at the bottom experiences this force in the vertical direction and the sides of the mountain are free. Therefore this is not a case of pressure or bulk
compression. There is a shear component approximately hpg itself.
Now the elastic limit fora typical rock is 30 x 107 N m2. Equating this to hpg, with
p =3 x 103 kg m-3 giveshpg = 30 x 107 Nm". Or
= 10 km
h = 30 x 10' N m/(3 x 10 kg mºx 10 ms)
which is more than the height of Mt. Everest
Posted from my blog with SteemPress : http://127.0.0.1:89/wordpress/2018/06/08/steempress-2-info-applications-of-elastic-avior-of-arts/
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://www.scribd.com/document/249635536/CBSE-class-12-physics-part1