Modelos Matemáticos | Ecuación de Difusión

Saludos queridos lectores, bienvenidos nuevamente a mi Blog. Cuando hablamos de Matemáticas la primera reacción es de temor, terror, desagrado para las personas que no les interesa el tema, más sin embargo, las Matemáticas es parte fundamental para muchas ciencias y sobre todo de la ingeniería. Estudiar las Matemáticas, requiere hacer uso del razonamiento lógico, para lograr en la práctica el desarrollo del razonamiento riguroso con objetos y estructuras puramente abstractos. Así, en esta oportunidad hablaremos acerca de la Ecuación de Difusión como modelo matemático. Las ecuaciones de convecció--difusión presentan numerosas aplicaciones en Ingeniería y Ciencias aplicadas. Por ejemplo, los procesos de convección natural se modelan a través de dichas ecuaciones. Estos procesos se originan cuando en un fluido se producen variaciones de temperatura, originando variaciones espaciales de densidad, lo que ocasiona que el fluido esté sometido a distintas fuerzas gravitatorias que pueden originar su movimiento. Los procesos de convección natural presentan numerosas aplicaciones en diversas situaciones, por ejemplo, cuando se tratan problemas de climatización en arquitectura, de contaminación marina (las más importantes suceden en la dinámica del océano y la atmósfera), de diseño de ventanas de doble cristal, en mecánica de fluidos, transferencia de calor, finanzas, entre otros.

Esta publicación esta dirigida a estudiantes, profesionales e investigadores en específico en el área de las Matemáticas Aplicadas e Ingeniería, y público interesado en estos temas interesantes para el entendimiento de buena parte del medio que nos rodea día a día. Estoy abierto a sus comentarios y dudas que puedan surgir dentro del tema. Sin perder más tiempo, comencemos.

Es importante recordar que para problemas del tipo hiperbólicos y elípticos, donde para una ecuación de segundo orden existen dos o ninguna dirección característica en cada punto respectivamente. Ahora bien, el tercer tipo de problemas, donde sólo existe una dirección característica, se denomina parabólico, y si esta dirección característica viene dada por t = C, donde C es una constante, entonces de la ecuación general lineal de segundo orden, podemos reducirla a la ecuación de la siguiente forma:

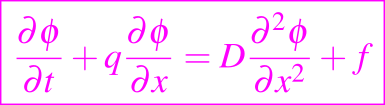
donde q, D y f son funciones que depende de x y t

Esta ecuación modela muchos fenómenos de la ciencia, donde normalmente a la variable t la asociamos con la variable del tiempo, de modo que t aumenta, y adicionalmente los datos iniciales son dados en t = 0. Para muchos problemas los coeficientes q y D son constantes, y se les denomina velocidad convectiva y coeficiente de difusión. En general, le valor de D será positivo, y por lo tanto puede ser escalado a uno; también para muchos problemas q = 0 y así se puede obtener la ecuación de difusión

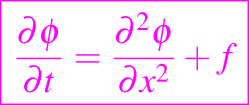
En un espacio de más dimensiones, la derivada parcial de segundo orden, es reemplazada por


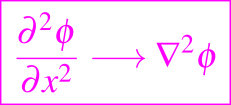
y la ecuación de difusión en estado estacionario se reduce a la ecuación de Poisson.

El ejemplo más común de difusión es la conducción de calor en un sólido, donde la conservación de energía con q = 0 conduce a la ecuación siguiente:

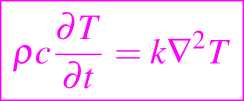
la cual es comunmente llamada la ecuación de conducción de calor.

Para un sólido en movimiento, la velocidad q, o para la conducción de calor en un fluido incompresible con una viscosidad insignificante, entonces el término convectivo

y la ecuación de difusión-convección dada al inicio es el modelo apropiado (con f = 0). Otro ejemplo de la mecánica de fluidos es el de un flujo viscoso unidireccional q = [0, 0, w(x, y)] como en una tubería o canal. Entonces la ecuación siguiente se satisface


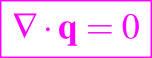
y así la ecuación siguiente


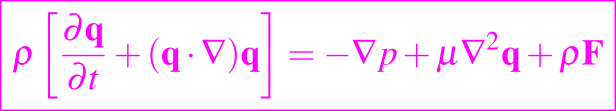
se reduce a


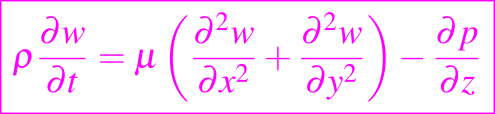
donde la derivada parcial de p con respecto a z es una función que solo depende del tiempo.

También se muestra fácilmente que en un flujo bidimensional la vorticidad

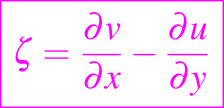
satisface la ecuación de difusión.

Un ejemplo más interesante es el de la difusión molecular, en la que dos sustancias coexisten en un elemento macroscópico de volumen en cada punto y sus proporciones relativas varían en el espacio y el tiempo. En el caso más simple, una de las sustancias, llamada matriz, es fija y la otra se difunde a través de ella con una concentración dada por c(x, t). Algunos ejemplos son un tinte en un líquido, humo en la atmósfera y humedad en un sólido seco; otros ejemplos son cualquier mezcla de sustancias como un soluto disuelto en un líquido o gas, y un material secundario en un metal que forma una aleación. Si estas mezclas están en equilibrio con la constante c, existe una relación termodinámica entre la temperatura, la presión y el potencial químico A(T, p, c) de la mezcla, de modo que la concentración de equilibrio se prescribirá en términos de p y T. Si hay equilibrio termodinámico pero c varía espacialmente, entonces el material secundario o el soluto se difundirá, y para pequeñas concentraciones c, el flujo difusional es j = -α grad A, donde α es positivo. Así j = -D grad c, donde

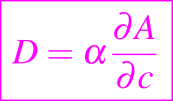
y a menudo se supone que es constante. Luego para la conservación del soluto tenemos


que es una ecuación de difusión. Nótese que en un líquido con convección de soluto j = cq -D grad c, y el término convectivo div(cq) aparece en la ecuación (1); para un líquido incompresible esto se reduce a


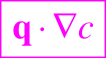
y c satisface la primera ecuación con f = 0.

Se pueden obtener condiciones suficientes para un problema de valor en la frontera bien planteado para la ecuación de difusión

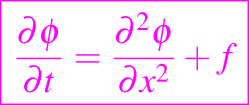
a partir del teorema del valor máximo para el dominio mostrado en la Figura siguiente


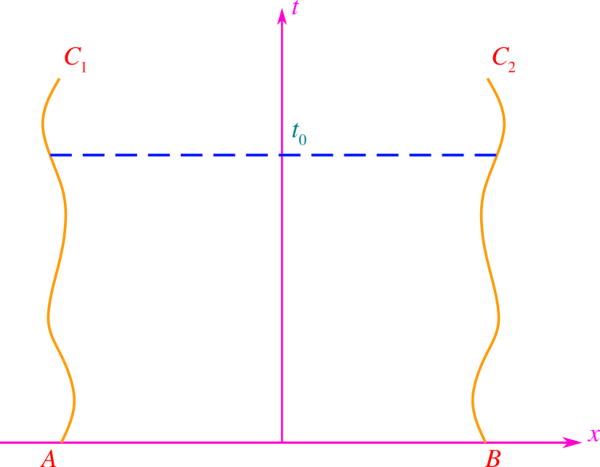
_{Dominio para problemas parabólicos bien planteados. Elaborada por @abdulmath, con Inkscape.}
con fronteras t = 0, t = t₀ > 0, C₁ y C₂, donde cada una de las curvas C₁ y C₂ intersecta líneas de constante t sólo una vez.

El teorema establece que para f menor o igual a cero, la función φ toma su valor máximo en t = 0, C₁ ó C₂. Para f mayor o igual a 0 hay un teorema de valor mínimo correspondiente, y un resultado de unicidad para el problema de Dirichlet siguiente: para φ = g(x) en t = 0, φ = h₁(t) en C₁ y φ = h₂(t) en C₂ (Si hubiera dos soluciones, su diferencia tendría un valor máximo y un valor mínimo de cero en la frontera y, por lo tanto, sería idénticamente cero). Además, las cotas de los pequeños cambios en los valores de la frontera para φ serán las cotas de los cambios consiguientes de φ en el interior de D. Por lo tanto, si las soluciones al problema de Dirichlet existen con los datos dados en la frontera abierta, entonces son únicos y dependen continuamente de los datos, por lo que el problema está bien planteado.

Para datos en fronteras más generales, tales como

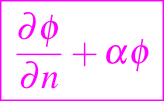
dados en C₁ y C₂, la unicidad sólo se puede establecer para α mayor igual a cero. También hay que tener en cuenta que si hubiéramos intentado resolver la ecuación de difusión en t < 0, es decir, hacia atrás en el tiempo, con datos dados en t = 0, el teorema del valor máximo permitiría que ocurriera un máximo en C₁, C₂, ó t = -t₀ < 0, y no seguiría ningún resultado de unicidad.

Para la ecuación de Poisson definimos la función de Green por la ecuación

pero para la ecuación de difusión, que no es autoadjunta, es más sencillo adoptar la definición dada por la ecuación


Así, G(x, t, ξ, η) satisface la ecuación adjunta en las variables ξ y η de modo que tenemos la siguiente ecuación:


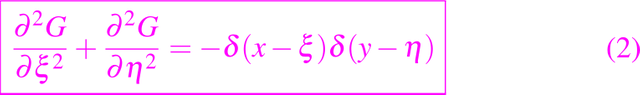
con G = 0 en C₁ y C₂ y cuando η tiende a infinito. Esta última condición de que G = 0 cuando η tiende a infinito, implica que G = 0 para η > t (usando el teorema de unicidad en la ecuación de difusión hacia atrás), y puede ser reemplazado por G = δ(x - ξ) en η = t donde ahora


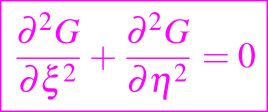
en η < t. Aplicando el teorema de Green en el dominio delimitado por C₁, C₂, η = 0 y t,


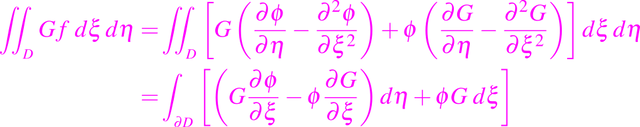
Evaluando esta integral de línea obtenemos


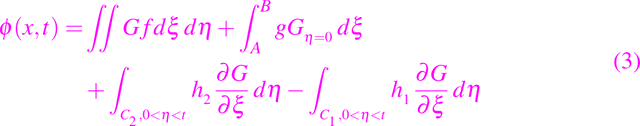
Esto da una expresión explícita para φ en términos de los datos de la frontera y de la función G de Green, que puede demostrarse que existe y que es única (para ello el lector intersado puede ver Stakgold (1979)). Muestra claramente que la solución en el momento t depende sólo de los datos dados en momentos anteriores.

La función G será singular en x = ξ, t = η es importante obtener la forma precisa de esta singularidad, que debe ser independiente de las condiciones de contorno C₁ y C₂. Así podemos considerar el problema en el medio espacio -∞ < ξ < ∞, η < t, y el problema para G es equivalente a resolver

si reemplazamos t - η por t y x - ξ por x. En un problema de conducción de calor esto modela la distribución de la temperatura en una barra infinita debido a un punto caliente localizado en x = 0 y t = 0, y a menudo se llama la distribución instantánea de la temperatura de la fuente de calor.

Encontramos φ tomando la transformada de Fourier en x dada por

Así


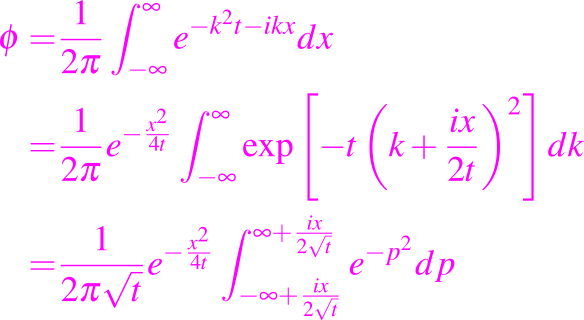
donde p = k + ix/2t.

Por el teorema de Cauchy esta integral compleja es equivalente a la integral a lo largo del eje real, porque la línea

no contiene ninguna singularidad del integrando, y tiene el valor raíz cuadrada de π. Así la solución fundamental de la ecuación de difusión es


que implica que el comportamiento singular de G cerca de x = ξ, t = η viene dado por

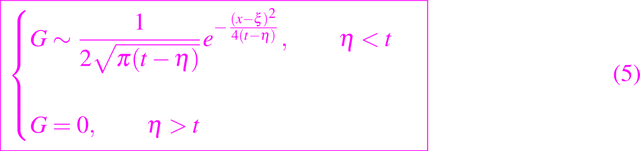
Con fronteras fijas hay muchos métodos numéricos disponibles que utilizan diferencias finitas tanto en x como en t, y marchan en el tiempo utilizando la propiedad de que la solución sólo depende de lo que ha ocurrido antes. En este sentido, los problemas parabólicos son más fáciles de resolver mediante métodos de diferencia finita que los problemas elípticos, en los que la solución depende de los valores en ambos extremos de cualquier malla en diferencias finitas.

El humo, que es una mezcla de gases y partículas, se difunde desde cualquier chimenea de altura h hacia la atmósfera y es conveccionado por los vientos dominantes. Se requiere un modelo que permita predecir la concentración del humo a nivel del suelo; y de particular interés, por razones de seguridad, es el valor máximo de la concentración de contaminante en el suelo. Los efectos de la gravedad no son importantes, y hay una capa de inversión en la atmósfera inferior a una altura d a través de la cual no hay transporte de humo. Tanto la velocidad del viento como el coeficiente de difusión variarán de punto a punto de forma aleatoria, pero consideramos escalas de longitud tales que estas cantidades toman un valor medio y cambian sólo con la altura. La ecuación de difusión convectiva de estado estacionario para la concentración c con coeficiente de difusión D es la siguiente

donde U es la velocidad media del viento que está en la dirección x, y z se mide verticalmente hacia arriba de modo que U y D son funciones de la variable z La concentración c debe desaparecer cuando y tiene a mas o menos infinito y buscamos la concentración transversal media


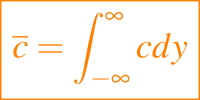
que al integrar la ecuación (1) se satisface


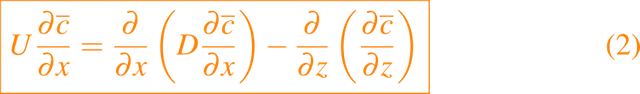
Las condiciones de frontera son


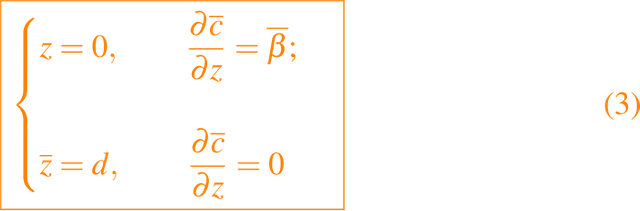
junto con


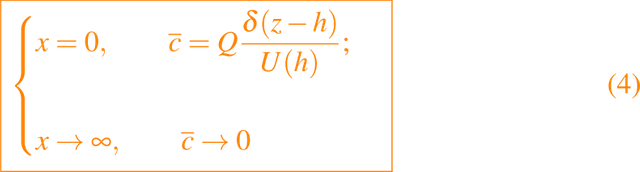
donde Q es la fuente de fuerza que emana de la chimenea. Si resolvemos este problema para c barra entonces una forma de evaluar c es asumir, debido a los movimientos aleatorios del aire, que hay una distribución normal de c en la sección transversal; es decir,


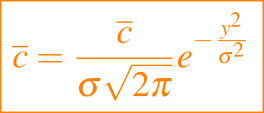
donde σ debe determinarse mediante experimentaación y puede esperarse que varíe lentamente con x y z.

Simplificamos aún más el problema bidimensional examinando la solución en una escala de longitud x que es grande en comparación con la altura de la chimenea h, y obviamos las segundas derivadas con respecto a x en comparación con aquellas con respecto a z para que la ecuación dada en (2) se reduzca a

y no se dan condiciones cuando x tieneda a mas o menos infitio. Esto ahora define un problema parabólico bien planteado para c donde x ha reemplazado a t como la variable del tiempo, y buscamos soluciones bajo diferentes supuestos para d, β, U y D. El problema más simple es tomar β = 0, d tendiendo a infinito y asumir que U y D son independientes de z. Entonces, con variables adecuadamente escaladas, el problema del valor en la frontera es


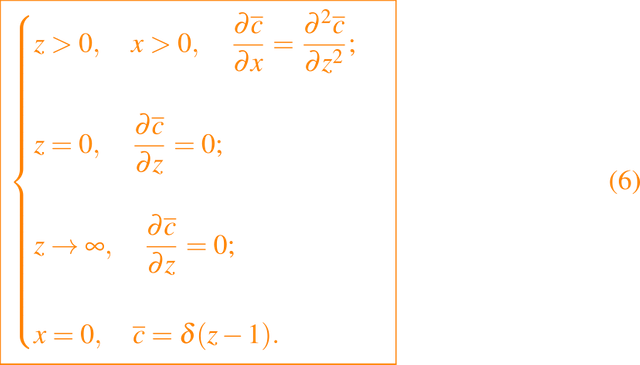
La solución se puede obtener utilizando una transformación Laplace en x, también se puede llevar a cabo en el caso de d finito. Más importante es considerar el caso cuando la tasa de deposición β no es insignificante. Para concentraciones pequeñas, la tasa de deposición será proporcional a la concentración, de modo que


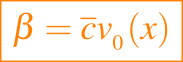
donde v₀(x) es la velocidad de deposición que varía con el terreno. El problema ya no puede ser resuelto por una transformación Laplace en x y se busca una solución en términos de una función de Green.

Queridos amigos y lectores, espero hayan disfrutado de una nueva publicación donde las matemáticas tienen sus aplicaciones en otros campos de la ciencia los cuales son de mucho interés en general. Espero que la misma haya sido de su agrado, y pueda servir de una ventana de apoyo para visualizar las estrechas relaciones que existen en particular entre las ciencias, así como se puede contextualizar las mismas teorías en la ingeniería, gracias por tomar un poco de su tiempo y poder disfrutar un poco más del maravilloso mundo de las matemáticas y las ciencias básicas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

1. Bender, C. M. and Orszag, S. A. Advanced mathematical methods for scientists and engineers. McGraw-Hill, New York. 1978.
2. Courant, R. and Hilbert, D. Methods of mathematical physics, vol. I. Interscience, New York. 1976.
3. Landau, L. D. and Lifshitz, E. M. Fluid mechanics. Pergamon, London. 1963.
4. Stakgold, I. Green's functions and boundary value problems. Wiley-Interscience, New York. 1979.

La imagen de fondo de la portada es una imagen de libre uso tomada de Pixabay y editada con GIMP por @abdulmath. Las imágenes son todas de libre uso, tomadas de Pixabay y editadas y tratadas con GIMP. Los títulos, imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, LaTeX2e, Inkscape y GIMP.

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.