Saludos y bienvenidos. Anteriormente en la primera parte hablamos de la representación del punto en doble proyección ortogonal y de cómo a partir de dos puntos conocidos podemos trazar una recta en el espacio y representarla en doble proyección ortogonal (a partir de ahora doble proyección ortogonal=DPO) a través de sus proyecciones horizontal y vertical.

Se acostumbra a denominar las rectas con una letra minúscula (Osers et al 2012). No debemos olvidar la nomenclatura específica para puntos (letra mayúscula) y rectas (letras minúsculas), además de utilizar siempre en DPO el superíndice “h” o “v” para cada punto o recta en su respectiva proyección (horizontal o vertical respectivamente).

Una recomendación importante a lo largo del estudio de la Geometría Descriptiva es adquirir el hábito de darle una denominación a cada elemento nuevo que se obtenga (recta, punto, plano, etc), ya que suele ser más difícil pensar en elementos que carecen de denominación (Osers et al 2012). Establecer un nombre a cada elemento ayuda a entender mejor su representación en la DPO y su ubicación en el espacio.

Rectas

Una vez conocidas las proyecciones horizontal y vertical de dos puntos podemos obtener una recta. En su defecto basta con conocer un punto y una dirección específica. Existen varios tipos de rectas dependiendo de su dirección y posición en el espacio. Algunos de estos tipos de recta más allá de poseer alguna particularidad geométrica, poseen aplicaciones importantes en procedimientos para resolver problemas métricos, por lo que también estos tipos de recta pueden ser vistos como herramientas que deben de comprenderse para poder utilizarse con efectividad.

Una recta cualquiera es el caso genérico, y consiste en una línea recta con dirección cualquiera tal como se observa en la Figura N°1.

_{Figura N°1: recta “a” cualquiera en el espacio y en DPO.}

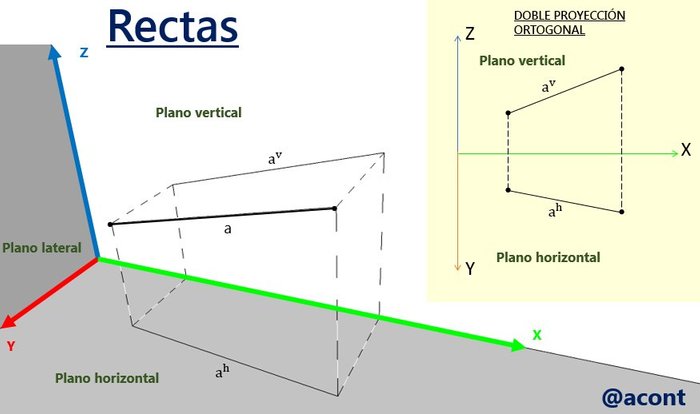
En el caso de una recta cualquiera representada en la DPO, cuyas proyecciones horizontal y vertical son conocidas, si se quiere hallar la proyección desconocida de un punto sobre esta recta conocida la restante, simplemente se traza una línea de referencia vertical hasta cortar la otra proyección de la recta (Figura N°2). Lógicamente, si un punto se encuentra sobre una recta en el espacio, en la DPO las proyecciones de dicho punto también estarán sobre las proyecciones de dicha recta.

_{Figura N°2: conocidas las proyecciones de la recta “a” y la proyección horizontal del punto “A”, para hallar la proyección vertical de “A”, se traza una línea de referencia hasta cortar la proyección vertical de la recta.}

Rectas horizontal y frontal

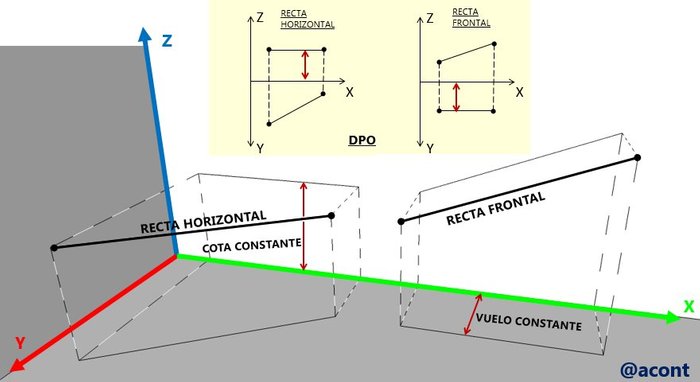
Estos tipos de rectas poseen una propiedad importante: en el caso de la recta horizontal, todos sus puntos poseen una cota constante; y en el caso de la recta frontal todos los puntos sobre ella poseen un vuelo constante. Es indispensable para el estudiante familiarizarse con los términos vuelo y cota. En la Figura N°3 observamos la situación en tres dimensiones y también representada en la DPO.

_{Figura N°3: rectas horizontal y frontal.}

Recta en el plano horizontal y recta en el plano frontal

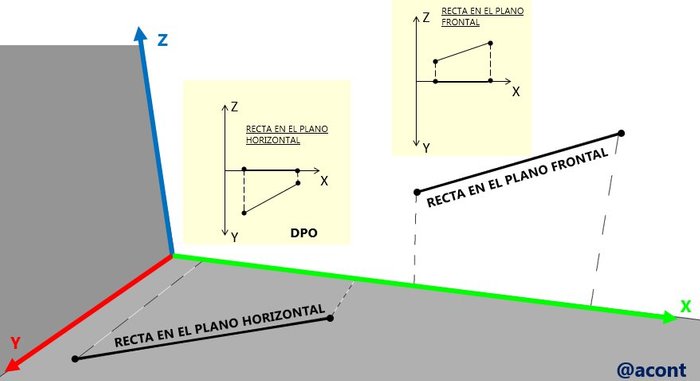
Más que otro tipo de recta, corresponden a un caso particular de las rectas anteriores. La recta en el plano horizontal es una recta horizontal de cota igual a cero. La recta en el plano frontal es una recta frontal con vuelo nulo. Es decir, cada una de estas se encuentran directamente sobre cada uno de sus planos (Figura N°4).

_{Figura N°4.}

Recta de punta y recta vertical

La recta de punta es paralela al eje Y, cuando se representa en la DPO, su proyección sobre el plano vertical será tan solo un punto, mientras que será totalmente vertical su proyección horizontal. La recta vertical es lo contrario, su proyección horizontal en la DPO es tan solo un punto. Podemos ilustrar claramente esto en la Figura N°5.

_{Figura N°5.}

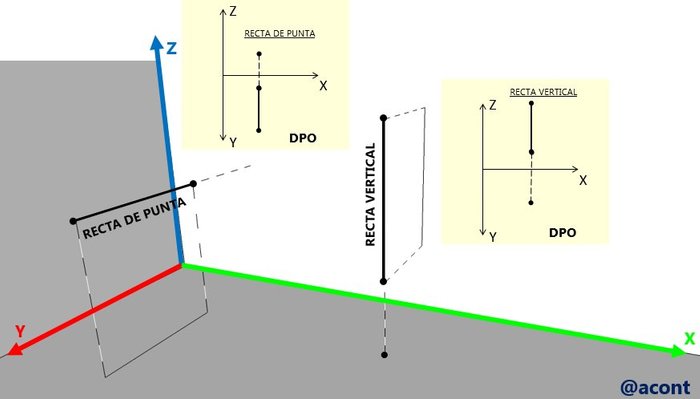
Cada una de estas rectas son un caso particular de las rectas horizontal y vertical respectivamente.

Recta paralela a la línea de tierra (eje X)

Esta recta es paralela al eje X (línea de tierra) por lo que en la DPO ambas proyecciones también lo serán (Figura N°6). Es un caso particular de las rectas frontal y horizontal.

_{Figura N°6}

Recta de perfil (recta lateral)

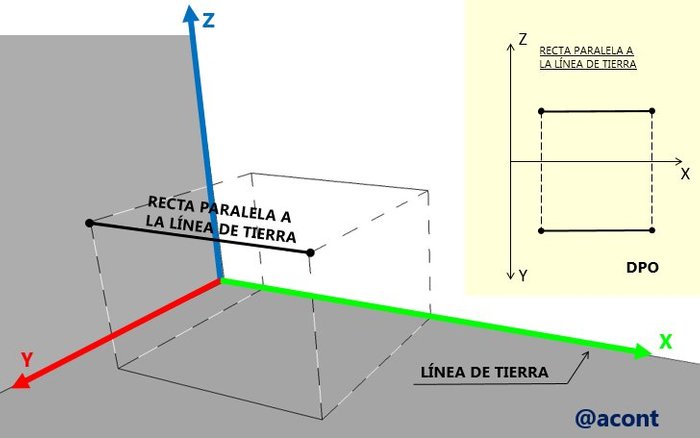
Este tipo de recta se caracteriza por ser paralela al plano lateral de proyección, por consiguiente, en la DPO se observará como una línea vertical ya que ambas proyecciones serán verticales. Un ejemplo de este tipo de recta se observa en la Figura N°7.

_{Figura N°7: recta de perfil.}

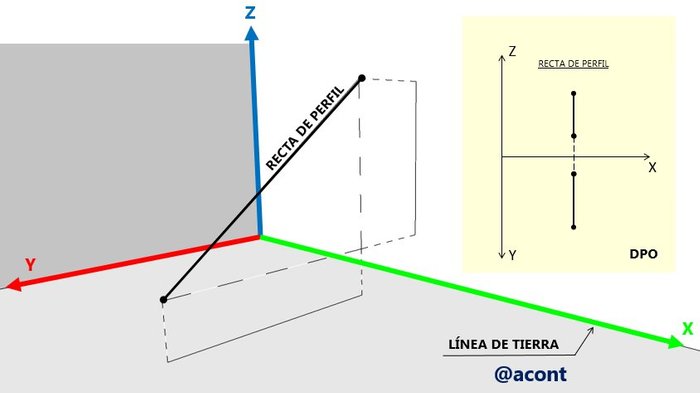
Al poseer cierta inclinación, es indispensable conocer al menos dos puntos sobre ella para poder definirse en el espacio a partir de la DPO. Es decir, su DPO no brinda información visual acerca de su inclinación, solamente al conocer dos puntos sobre ella podemos conocer su dirección a través del procedimiento que veremos a continuación, el cual se le suele llamar movimiento de puerta o cierre de puerta.

Supongamos que conocemos dos puntos “A” y “B” sobre una recta de perfil y queremos obtener una representación visual de su dirección en la DPO. Si representamos esta recta en el espacio, su dirección se puede observar claramente, mientras que en la DPO esto no es así (Figura N°8).

_{Figura N°8.}

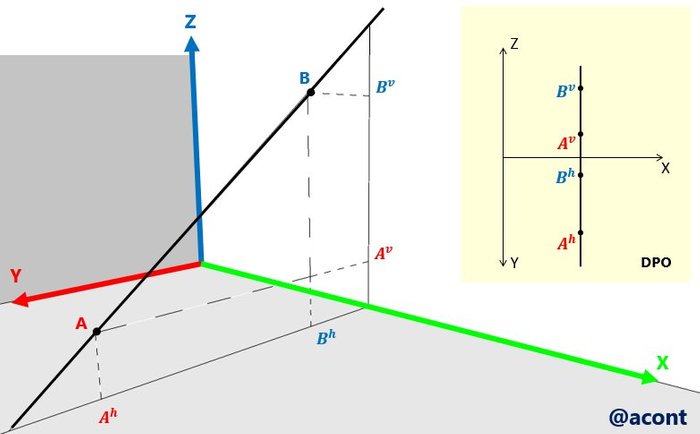
El procedimiento del cierre de puerta, consta de hacer girar la recta de perfil alrededor de un eje determinado para así ver su proyección en uno de los dos planos de proyección (horizontal o vertical). En este ejemplo, haremos girar la recta alrededor de una recta vertical en el plano vertical. En la Figura N°9 observamos una ilustración de este “cierre de puerta”.

_{Figura N°9}

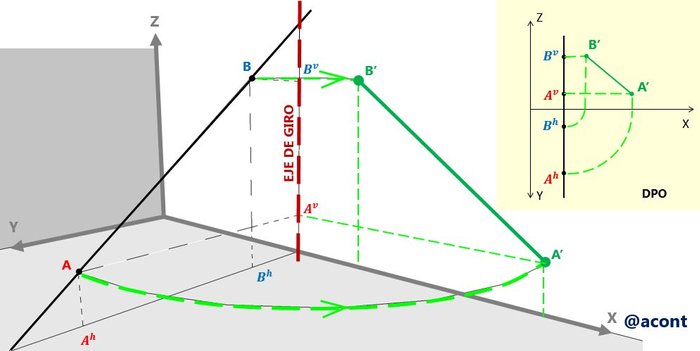
De esta manera hemos ubicado la recta de perfil en el plano vertical de proyección. En la DPO podemos observar claramente la recta de perfil representada sobre el plano vertical, de esta manera podemos apreciar su inclinación. No obstante, no debemos olvidar que esta no es la ubicación real de esta recta sino más bien una vista de la misma desde el plano lateral.

Si conocemos la proyección vertical de un punto “C” sobre esta recta de perfil y queremos ubicar su proyección horizontal debemos aplicar el mismo procedimiento, pues debemos primero reflejar la proyección vertical de “C” sobre la recta “girada” y luego seguir una trayectoria paralela a la de los puntos “A” y “B” hasta cortar con la proyección horizontal de la recta de perfil, encontrando así la proyección horizontal del punto “C” (Figura N°10).

_{Figura N°10}

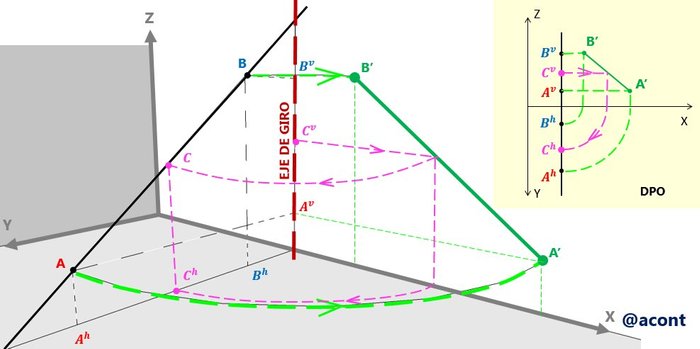
Cabe destacar que el “giro” de la recta de perfil pudo haberse efectuado alrededor de una recta de punta en el plano horizontal, el procedimiento sería similar solo que el movimiento se daría al revés. No necesariamente el ángulo de rotación debe de ser un ángulo recto y el eje de rotación tener vuelo o cota cero (Osers et al 2012). Esto último se refiere a problemas particulares de rectas de perfil.

Trazas de una recta

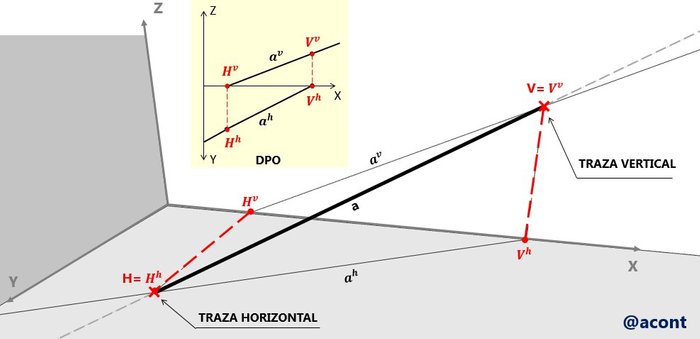
Las trazas de una recta corresponden simplemente al punto de corte de una recta con cada uno de los planos de proyección. La traza horizontal “H” es el punto de corte de una recta con el plano horizontal de proyección. Lo mismo para la traza vertical “V” con el plano vertical de proyección. En la DPO, el uso de estos dos puntos es importante en ciertos procedimientos, por lo que se debe tener claro que representan las trazas de una recta y como ubicarlas. En el artículo anterior se abordó la representación de las trazas “H”, “V” y ”L” de una recta dada. La traza lateral ”L” no suele utilizarse en la DPO. Para ubicar las trazas de una recta “a” en la DPO, se debe ubicar el punto donde cada proyección de la recta corta con la línea de tierra (eje X).

_{Figura N°11}

Cuadrantes que una recta atraviesa

Nos referiremos al ejemplo de la recta anterior (Figura N°11). En la Figura N°12 podemos observar en el espacio los cuadrantes que dicha recta atraviesa. Una recta en el espacio puede atravesar como mínimo 3 cuadrantes (Osers et al 2012). De esta forma, dependiendo de la ubicación de los puntos de dicha recta en la DPO podemos observar que cuadrantes atraviesa la misma (ver Figura N°6 de la Parte I de la presente publicación).

_{Figura N°12}

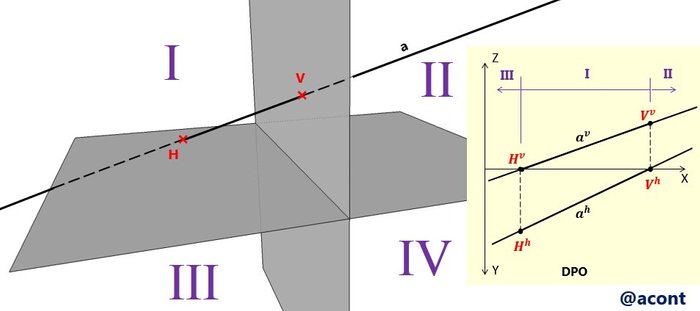
En la DPO los puntos de la recta “a” cuya cota y vuelo son positivos se encuentran en el primer cuadrante. Los puntos de dicha recta que tienen vuelo negativo y cota positiva están por detrás del plano vertical de proyección, es decir, el segundo cuadrante, puesto que esto ocurre a la derecha de la traza vertical “V” en la DPO. Finalmente, los puntos de la recta que se encuentren a la izquierda de la traza horizontal “H”, tienen cota negativa y vuelo positivo, indicando que la recta atraviesa el tercer cuadrante a lo largo de este sector de la misma.

Aportes de esta publicación

Se aporta material que nos ilustra las propiedades y tipos de rectas en Geometría Descriptiva a través de ilustraciones que abarquen la situación tanto en tres dimensiones como en el plano, logrando así comprender de manera más efectiva la doble proyección ortogonal.

---

Referencias Bibliográficas

Osers et al (2012). Estudio de Geometría Descriptiva (14va Edición). Editorial Torino. Caracas._{Fuente para consulta (doceava edición)}

Material recomendado

Di Pietro, Donato (1985). Geometría Descriptiva. Editorial Alsina. Buenos Aires.

Izquierdo Asensi, F (1957). Geometría Descriptiva. Editorial Paraninfo. Madrid.

---

Imágenes de autoría propia, realizadas mediante el programa SketchUp 8 y posteriormente editadas con Microsoft PowerPoint.

---

Publicado mediante SteemSTEM.io