[Let's learn math #2] Discussing Bounded and Unbounded sequence....
Bounded and Unbounded sequence

What are Bounded sequence??
A sequence is bounded if we can restrict the size of all its terms....
In field of real analysis a sequence {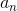.gif) } is bounded if :
} is bounded if :
- It is bounded above i.e. there exist a real number
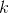.gif) such that:-
such that:-
.gif)
where 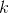.gif) is called upper bound of sequence {
is called upper bound of sequence {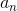.gif) }
}
- It is bounded below i.e. there exist a real number
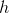.gif) such that:-
such that:-
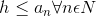.gif)
where 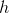.gif) is called lower bound of sequence {
is called lower bound of sequence {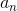.gif) }.
}.
So a sequence is bounded if it is bounded above as well as bounded below i.e. there exists two real numbers 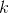.gif) and
and 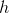.gif) such that:-
such that:-
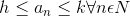.gif)
What are Unbounded sequence??
A sequence {
} is said to be unbounded , if it is not bounded.
In field of real analysis, a sequence {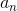.gif) } is said to be unbounded if given
} is said to be unbounded if given 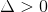.gif) , however large, there exist
, however large, there exist 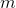.gif) belongs to natural number such that:-
belongs to natural number such that:-
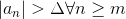.gif)
Graphical difference between Bounded and Unbounded sequence
Graphically we can say that a sequence will be bounded below if we draw a horizontal line such that all the points representing the sequence stay above from that line. Similarly, a sequence is said to be bounded above if we can draw a horizontal line such that all the points representing the sequence stay below from the line.
Now a sequence is said to be bounded if it is closed between two horizontal lines of bounded above and bounded below and a a sequence is said to be unbounded if only one line i.e. either bounded above or bounded below exist or non horizontal line exist.
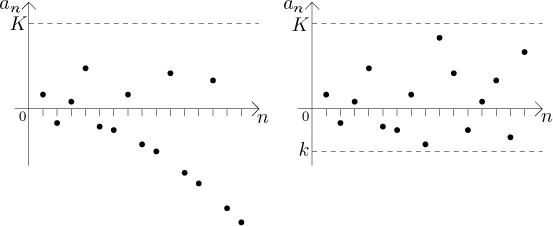
It is clear from the above image, left side graph is bounded above ( see a dotted horizontal line ) but is not bounded below, so left graph is showing an example of Unbounded sequence and the right side graph is both bounded above as well as bounded below ( see one horizontal dotted line above points representing as bounded above and one dotted horizontal line below points representing bounded below) so the right side graph is an example of Bounded sequence.
What is least upper bound and greatest lower bound
The number which is smallest from all upper bounds is called as least upper bound whereas the number which is greatest from all lower bounds is termed as greatest lower bound.
The least upper bound is called as Supremum whereas greatest lower bound is called as Infimum.
Solving problem on Bounded sequence
Problem:-1) Prove that the sequence {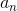.gif) } = {
} = {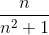.gif) } is bounded.
} is bounded.
Solution:- So according to simple definition of bounded sequence, a sequence is bounded if we can restrict the size of its terms.
So , here we will try to do so:-
Given:- {.gif) } = {
} = {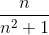.gif) }
}
which implies,
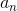.gif) =
= 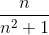.gif)
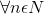.gif)
Therefore,
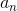.gif) =
= 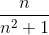.gif) =
= 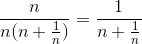.gif)
Now
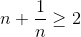.gif)
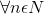.gif)
Therefore,
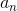.gif) =
= 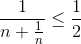.gif)
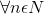.gif)
Also
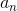.gif) =
= 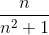.gif) >0
>0 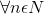.gif)
Therefore, we restricted the size of sequence i.e.
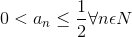.gif)
Here 0 is lower bound and 1/2 is upper bound of given sequence, hence proved that given sequence is bounded.
Solving problem on Unbounded sequence
Problem:2) Prove that the sequence {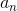.gif) } = {
} = {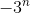.gif) } is unbounded sequence..
} is unbounded sequence..
Solution:- Here
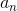.gif) =
= 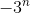.gif)
Let 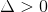.gif) , however large :-
, however large :-
Now
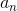.gif) | = |
| = |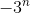.gif) | =
| = 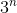.gif)
Now
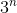.gif) >
>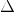.gif)
if
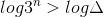.gif)
if
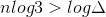.gif)
if
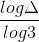.gif)
Therefore, |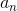.gif) | >
| > .gif)
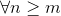.gif) >
> 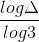.gif) where
where .gif)
Hence proved that given sequence is Unbounded.
Citations:-
(https://pixabay.com/en/math-blackboard-education-classroom-1547018/) background image of 1st image.
Definition of bounded and unbounded sequence(http://math.feld.cvut.cz/mt/txta/1/txe3aa1b.htm)
(http://math.feld.cvut.cz/mt/txta/1/txe3aa1b.htm) graphs are taken from here only first graph.
Problems are taken from a book not available online, whereas solutions are mine.
Oh, i just read this when it is almost midnight here and now I feel confused with this info!
So what is confusing you friend???