Lorentz Transformation
Lorentz transformation (Hendrik Anton Lorentz, 1853-19289)

Source
The invariance of the speed of light openly contradicts the laws of Newtonian mechanics and constitutes the starting point of the theory of relativity, formulated by Einstein. In Newtonian mechanics, it is stated that all coordinate systems are at rest or animated by a rectilinear movement that is uniform in relation to each other and, therefore, governed by the same physical laws; that is to say, that the laws of mechanics present the same form in all the inertial or Galileo systems of this genre. It will be seen now what modifications have to be introduced in the laws of classical mechanics to accept the new experimental facts.
Two observers E and E' are considered. The first, E, in a system of fixed axes, with origin in O; and the second E', in a system of moving axes, O', which moves in the direction of the x axis to the velocity v.
At the initial instant, O and O' are assumed to coincide. At any time, the origin O' is defined by the abscissa O on the moving axes and vt on the fixed axes. On the other hand, the origin O is defined by the abscissa -vt in the moving axes and by O in the fixed axes.
Any point P is defined, at time t, by its abscissa x (measured by E ), or by its abscissa x' measured by ED'. According to classical mechanics, x and x' are linked by the relationship, at first glance evident:
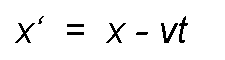
That is:
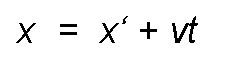
This relationship is called Galileo transformation and is based on the assumption that the clocks of the two observers are not influenced by the relative movement they present with respect to each other so that at all times it is:
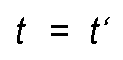
According to the Galileo transformation, the light should not have the same propagation velocity for E as for E ' . But the experience strongly contradicts such a consequence, deduced from classical mechanics. As Einstein pointed out, the correct interpretation of the facts obliges us to admit that t ≠ t ' ; that is, the movement of an observer, without his being able to realize it, affects the progress of his watch. The problem of replacing the Galileo transfer with another that satisfies the invariance condition of the speed of light c is presented, so that it is:
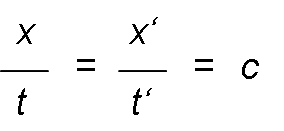
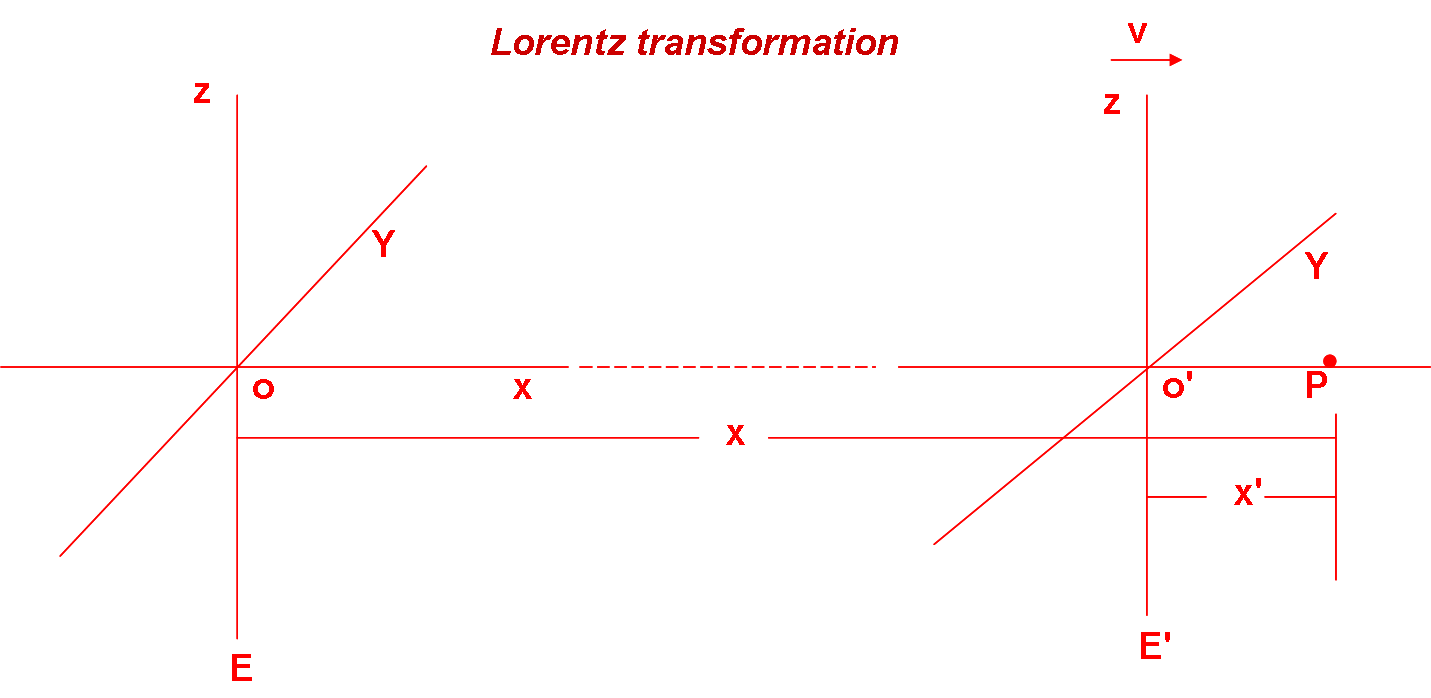
In summary, we try to calculate x ' and t', data observed by E ' and that define the situation of an event in space and time, from the data x and t measured by the fixed observer E about its event.
It will be admitted that there is no privileged observer, so that the transformation formulas must be invariant, to pass the data from E to E ' and vice versa. Just change the sign of the relative velocity v. The relations that define x ' and t' constitute the so-called Lorentz transformation (Hendrik Anton Lorentz, 1853-19289) and are the following:
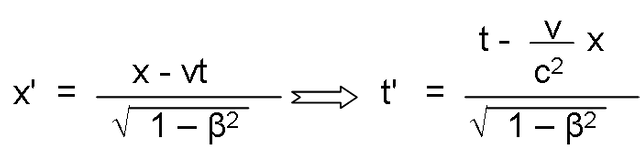
Being:
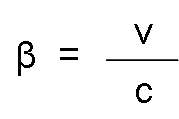
Where c is the speed of light.
In the aforementioned Lorentz transformation, three details immediately come into view: first, a length in the direction of the coordinate axis x ' is, relative to the coordinates x, "contracted" by the contraction factor:
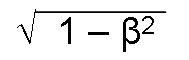
Second, a contraction of time produced by the fact that the passage of time is different in the two systems; and finally, that the velocity v can never be greater than c, since the expressions x ' and t' would then be imaginary.
References:
- http://hyperphysics.phy-astr.gsu.edu/hbase/Relativ/ltrans.html
- https://users.physics.ox.ac.uk/~smithb/website/coursenotes/rel_A.pdf
- https://newt.phys.unsw.edu.au/einsteinlight/jw/module4_Lorentz_transforms.htm
- https://thecuriousastronomer.wordpress.com/2013/03/10/derivation-of-the-lorentz-transformations-from-first-principles/

Congratulations @anarangel! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP