Maxwell's Demon: Violation of The Second Law of Thermodynamics
One of the major law of nature is the second law of thermodynamics. Actually, there are altogether four laws of thermodynamics but the second law is the most interesting one. This article is about a thought experiment which seems to violate the second law of thermodynamics! Yes, you heard me right. This sounds like something a flat-earther would say but this thought experiment was devised by none other than the famous physicist, James Clerk Maxwell.

First, Let's get familiar with the second law of thermodynamics.
The total entropy can never decrease over time for an isolated system.
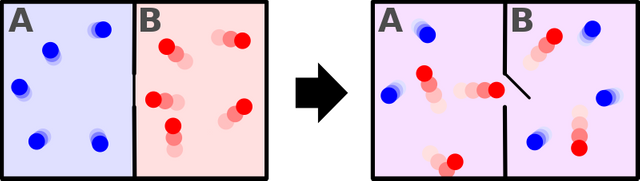
There are many ways of stating the second law but I will stick to this one. The statement above means that heat energy will never flow spontaneously from a cold object to a hotter one. Take a look at the picture below, there are two compartments each with air at a different temperature. The compartments are separated from each other by a thermally insulated wall with a small door, which is closed for now. let's say the blue one is at 10 °C and the red is at 50 °C. What happens when we open the door connecting the compartments? General intuition tells us that the air at 50 °C loses its heat energy to the other one until the system acquires a thermal equilibrium. This "General Intuition" is, in fact, the second law of thermodynamics. The second law is all about the direction of the flow of heat energy. From entropic point of view, the system changes from an ordered state to a disorder one. Up to now, we haven't violated any laws but will the disordered state go back to the ordered on its own? The second law tells us that it won't but Maxwell's demon tries to defy the second law. Yes, in the thought experiment devised by Maxwell, the entropy increases! Before we dive into the thought experiment, we need to understand a bit about the concept of temperature.
Temperature
We relate temperature with hotness and coldness but from a scientific perspective, the words don't have any meaning. A summer day at 40 °C feels hot for us but in comparison with the temperature of the sun, our summer day is too cold. To avoid this relative conundrum, we use a scientific definition of temperature. Quantitatively, we define temperature as:
The measure of the average kinetic energy of molecules.
Molecular vibration of a segment of protein alpha helix by Greg L,CC BY-SA 3.0
Kinetic energy is the measure of the vibration and movement of the molecules of a system. In the case of a solid object, the molecules are constantly vibrating and higher the temperature, higher is the amplitude of vibration. Similarly, for a gas, the temperature is the measure of movement of the molecules. This is described by the kinetic theory of gases. The universal scale of temperature measurement, which is the Kelvin scale, is based on this definition of temperature. As the temperature decreases the vibration/movement of molecules decrease and eventually we reach a state when the vibration completely ceases. This temperature is the zero Kelvin.
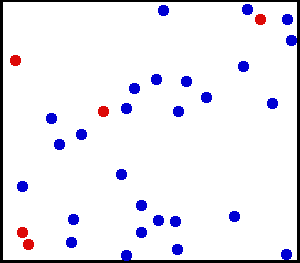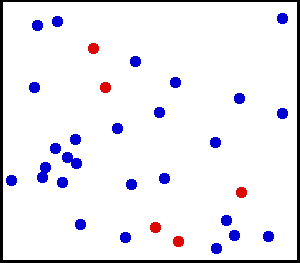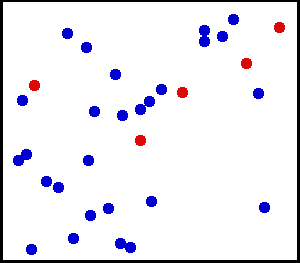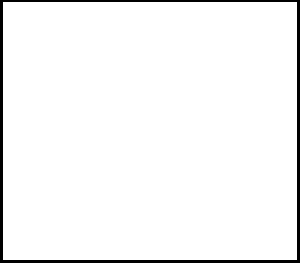
Motion of gas molecules by Greg L, CC BY-SA 3.0
If you look closely at the definition of temperature, we have used the term average kinetic energy of molecules. This plays a crucial role in our thought experiment, pay more attention to this :) Let's say we have air at 25 °C. Since the temperature is above zero kelvin, there will be movement of molecules and the molecules have a certain amount of kinetic energy but do all molecules have the same kinetic energy, i.e. do all molecules move with the same velocity? The answer is no, they don't. Look at this gif picture of gas molecules constantly moving and colliding with each other. The movement and collision are random processes and the molecules have different velocity at each instant. There are countless numbers of molecules, so how can we know the velocity of each molecule? For this, we use the Maxwell–Boltzmann distribution
Maxwell–Boltzmann distribution
We have established the fact that gas molecules don't move with the same speed and now we want to know the speed of those molecules. Is it possible though? There may be millions of molecules and we don't have any deterministic way to find the velocity of each molecule. To solve this, Maxwell and Boltzmann ( independently) formulated a statistical method. I won't go behind the mathematics of Maxwell-Boltzmann distribution but a graph of the distribution will be enough to understand the general principle.
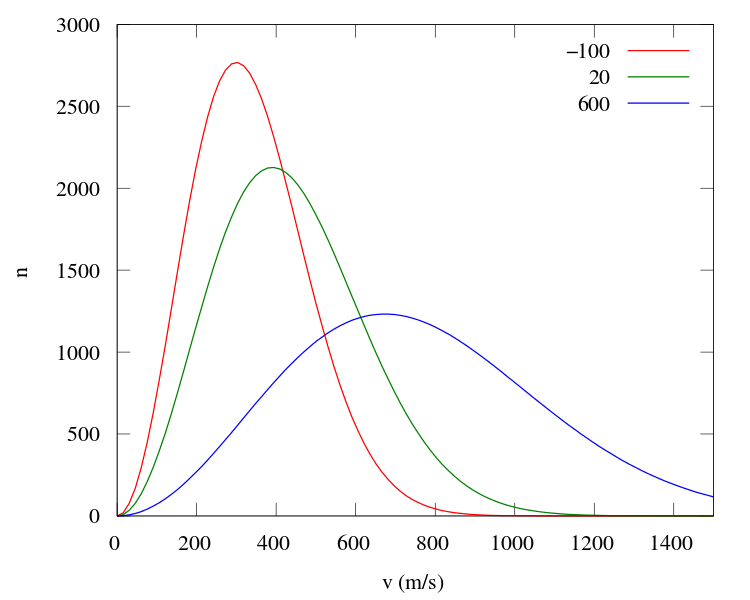
The horizontal axis shows the speed of Oxygen molecules, the vertical axis shows the number of Oxygen molecules and the three different coloured plots are for three different average temperature.
Red: -100 °C
Green: 20 °C
Blue: 600 °C
This is actually a probability distribution and it gives us a probability of finding molecules at a specific temperature range. Let's look at the red one. The average temperature of the red is -100 ° C. At this temperature the average speed of the molecules is 338 m/s but we know that all molecules won't move at this speed. Since the peak is at 300m/s, we will find most molecules moving at this speed but there are also those molecules which are moving much slower or faster than the average speed. For example, there are around 100 molecules moving at 800 m/s, which is much faster than the average speed. There are also slow-moving molecules. The fact that not all molecules move with the average speed is the key concept used in Maxwell's thought experiment.
Maxwell's Demon
In his book Theory of heat (1872), Maxwell wrote about a being that could violate the second law of thermodynamics:
... if we conceive of a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are as essentially finite as our own, would be able to do what is impossible to us. For we have seen that molecules in a vessel full of air at uniform temperature are moving with velocities by no means uniform, though the mean velocity of any great number of them, arbitrarily selected, is almost exactly uniform. Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower molecules to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics.
Theory of heat, p. 338 [1]
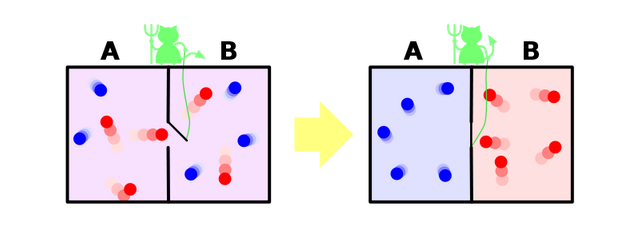
This being was later dubbed as "demon" by Lord Kelvin because it would cause serious havoc by breaching one of the fundamental laws of nature [2]. Look at the picture below. There are two compartments each with air at the same temperature, let's say 50°C. There is a molecular-sized mass less door connecting the two compartments and the demon is in control of the door. This so-called demon isn't something you would see in movies or paintings. The demon is actually an entity that has the ability to know the temperature of each molecule. Think it as a nano-scale sensor. We have already established the fact that there are molecules which move much slower or faster than the average speed. Now comes the role of the demon. Since the demon has the ability to know the temperature of each molecule, it will open the door in a such a way that fast molecules(reds) will travel to the right compartment and slower molecules (blue) will travel to the left compartment. In the end, we have a system of two compartments with air at an unequal temperature and the demon did this without using any external source of energy. The second law doesn't allow this. Think about the refrigerator, it transfers heat from a hot region to a cold region but it uses electric power to do this. On the other hand, the demon did the same thing without using any source of energy. Voila! We violated the second law of thermodynamics. This means free energy! we can finally have perpetual machines, no more environment unfriendly fossil fuels. Sadly no, we won't have any perpetual machines. We can't let a demon defy our precious second law, and finally the exorcism.
Exorcism
I would love to see a perpetual machine but mother nature won't let that happen. The second law has to be true, so where did the thought experiment fail? Before going into exorcism we should know that Maxwell never intended it to breach the second law practically. He wanted to convey an idea that through molecular manipulation one could fail the second law. Without further ado, let the exorcism begin! The first argument that comes to mind in the existence of the demon. Can a molecular level demon capable of measuring the temperature of each molecule even exist? Practically such thing doesn't exist but we are more concerned with the measurement of temperature with such precision rather than the size of the demon. During our whole analysis, we haven't talked about the work done by the demon to measure the temperature. No matter how the demon measures the temperature, energy has to be used. The measurement of temperature increases the entropy by more amount than the demon could decrease the entropy by switching the molecules. Physicists were confident that measurement process would generate entropy and they assumed the demon to be dead.
The demon was revived when Leo Szilard (in 1929) developed a hypothetical engine in which a demon appears to lower the entropy of a heat engine with a single molecule as working fluid [3] I will briefly explain about the Szilard's engine.
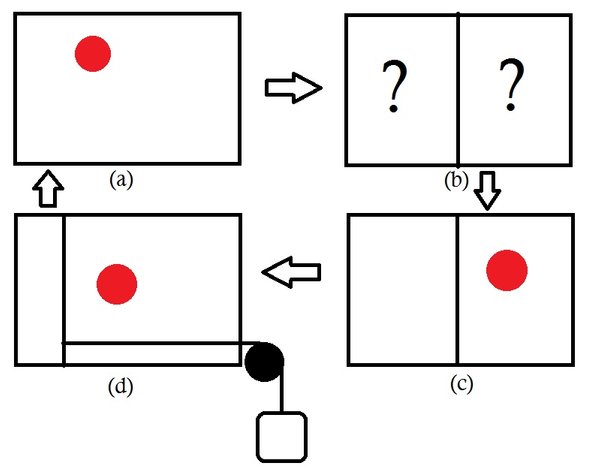
The engine consists of a single molecule as a working fluid and of course, there is a demon (a). The job of the demon is to figure out in which half of the box is the molecule located(b). Let's say the demon finds that the molecule is on the righthand side, now the demon quickly places a partition and attaches a piston on the righthand side(c). Due to the presence of molecule on the righthand side, the piston moves to the left and work is done on the load attached to the piston. Finally, the piston can be removed and the system is back to the original state(d). In this cyclic process, the engine extracts some heat energy and converts it to an equal amount of work (It can be shown that the amount of heat generated is kTln(2) ). Out of nowhere, the engine converted the thermal energy of the molecule into mechanical energy (work). The second law doesn't allow this, so one has to be wrong. Is it the second law or the Szilard's engine? You may argue that the work has to be done to insert and remove the piston. Yes, in practice work has to be done but in principle such processes can reversible and no entropy will be generated. The only option left to save the second law is again the measurement of the position of the molecule. Brillouin showed that entropy is generated to measure the position of the molecule via light signals [4]. Brillouin argued that the work generated by the engine is used to measure the position of the molecule and this is enough to save the second law. This turned out to false sigh the demon hasn't died yet. You may also wonder what's so special about the Szilard's engine? Technically, it's not much different than the original Maxwell's demon but the observations made by Szilard later turned out to be the foundation of information theory. The driving force behind the Szilard's engine is the information of the position of the molecule and the decision made by the demon is a binary operation. In a way, we can say that Szilard related information with the binary operation long before the existence of modern computers.
Finally, the last exorcism was done when R. Launder (in 1961) published his paper, Irreversibility and Heat Generation in the Computing Process [5]. Szilard had only considered the entropy generation during the measurement process but overlooked the role of memory of the demon. The Szilard's engine completes its cycle by returning to its initial state but the memory of the demon hasn't returned to its original state! The demon has to erase its memory before the next cycle begins. Launder showed that the process to erase a memory generates entropy. He also calculated the entropy generated to erase a bit of information to be k ln(2). Finally, Bennett applied this to destroy the century-old demon. Bennett (in 1973) proved that the measurement process can be reversible, so no entropy is generated in measurement[6]. Actually, the work generated by Szilard engine is employed in the memory erasure, not the measurement process. Finally, at the age of 101, the demon died. One thing to note is that although information erasure is not a reversible process, information transfer is reversible. We battled with the demon for over a century and the most important principle that we discovered from that is:
When we erase information, heat energy is generated.
Information is Physical
A striking conclusion was later by Launder in his famous statement, Information is a Physical Entity [7]. This may sound counterintuitive because we always think information as an abstract entity. His argument was that information is physical because it is always stored in a physical medium and is bound by the possible restrictions of the physical universe. We store information in a physical system, whether it is a piece of paper or a solid state drive, and the laws of physics (both classical and quantum) govern the properties of these devices, which in turn limits our capabilities for information processing. Launder himself related entropy with information, and just like entropy, information is a physical quantity that is governed by the laws of physics. The fact that information processing capabilities differ in two realms of physics, i.e. Classical and Quantum, sparkled the Quantum information theory.
Final words
Everything we have discussed so far is completely in theoretical realm but scientists have actually verified it through experiments. Back in 2010, Japanese Physicists generated energy out of information! They created their own version of Szilard's engine and using a high-speed camera (the demon), they made a molecule climb up a spiral staircase. I won't explain the working principle of their apparatus but you can read more about it here.
Maxwell would have never imagined the impact his demon made on the way we understand entropy and information. Maxwell's idea of the demon was to illustrate the statistical nature of a thermodynamic system but the demon lurked for a century to haunt generations of physicists.
References:
1. Maxwell, J. C. (1908). Theory of Heat.
2. Thomson, W. (1966). The Kinetic Theory of the Dissipation of Energy. Kinetic Theory.
3. Szilard, L. (1964). On the decrease of entropy in a thermodynamic system by the intervention of intelligent beings. Behavioral science.
4. Brillouin, L. (1951). Maxwells Demon Cannot Operate: Information and Entropy. I. Journal of Applied Physics
5. Landauer, R. (2000). Irreversibility and heat generation in the computing process. IBM Journal of Research and Development.
6. Bennett, C. H. (1982). The thermodynamics of computation—a review. International Journal of Theoretical Physics.
7. Landauer, R. (1999). Information is a physical entity. Physica A: Statistical Mechanics and its applications.
8. Bennett, C. H. (1987). Demons, engines and the second law. Scientific American.
9. Hemmo, M., & Shenker, O. R. (2012). The Road to Maxwell's Demon. Cambridge: Cambridge University Press.
10. Information Processing and Thermodynamic Entropy

SteemSTEM is a community project with the goal to promote and support Science, Technology, Engineering and Mathematics on the Steem blockchain. If you wish to support the steemSTEM project you can:
Contribute STEM content using the #steemstem tag | Support steemstem authors | Join our curation trail | Visit our Discord community | Delegate SP to steemstem
Very well written and explained. I liked the metaphor of the Demon, and a bit of science history.
Thanks! Demons are quite popular in physics. There is another famous demon called Laplace's demon which is as interesting as this one.
Excellent post This is very interesting, I am Mechanical Engineer and I really liked your article. I will follow you
Thank you :D
That is a very interesting thought experiment.
I kept thinking how this hypothetical being (Maxwell's Demon) would need energy in order to observe, perceive, decide and perform all those tasks (processing information - opening and closing the gate etc).
Even if we could create some sort of artificial intelligence, with say all technical requirements and equipment necessary to observe and measure the precise temperature and speed of molecules, wouldn't it still need some sort of external energy source in order to operate? Just a few thoughts.
Thank you for this wonderful read.
@lordneroo, Excellent question!
Yes, the process of measuring the temperature and opening/closing of the door requires some finite amount of energy. There are two aspects of this, energy consumption and entropy generation. Let's tackle them separately.
In principle, there isn't a theoretical limit for the energy required to open/close the door and for the measurement. The door can be made arbitrarily small and with appropriate material, its mass can be close to zero. Let's say the demon generates a thermal potential energy of 50 Joule by switching the molecules but in principle, the energy required for opening/closing the door (and of course the measurement) can be less than 50 J. There isn't any law of physics that doesn't allow this to happen. Hence, the second law fails (if we don't consider the role of the demon's memory).
Entropy generation is another problem of door opening/closing and measurement process. The second law tells us that either entropy has to remain constant or it has to increase. The demon lowers the entropy of the system by reducing the disorderness. So according to the second law, at least an equal amount of entropy has to increase to compensate the entropy reduced by the demon. Naturally, we think that the mechanical operation of door opening/closing and the measurement process increases the entropy. In real life, those operations indeed increase entropy but in principle, we can do those operations without increasing any entropy! Again the second law fails( if we don't take consider the entropy generated to erase the demon's memory).
Thanks for passing by. I love your Cartography series :)
Hey @anevolvedmonkey, thank you so much for taking the time to leave such a detailed, lengthy response. I truly appreciate that! Thanks for clarifying things and keep up the quality work.
PS: Thank you so much for your kind words regarding my work. The same goes to you of course!
Take care ! :)
Sincerely, i never understood the second law of thermodynamics until now (hated physics class back in school), this post presented it at its simplest, and after understanding it, i became even more intrigued that the law could be violated...., maxwells demon seemed great..., but then, ouch, the demon was exorcised.
Anyways, i'm glad i read this post, i love it when i finally understand something i thought i'd never get to understand. Thanks for enlightening me
Yes, the concept of entropy and the second law are one of the most confusing topics in classical physics. I am glad that this post helped you understand them more closely. Thanks for passing by! :)
Excellent post, and definitely worthy of the Steemstem resteem! I hadn't seen the entropy of changing a bit explicitly spelled out before (even though I guess it follows naturally from S = k*lnW). Thanks for the well-thought-out post!
Thanks, @proteus-h! Yes we can get the entropy generated from the erasure of a single bit from Boltzmann equation( S=kln(W)). In Szilard's engine, if we consider the microstates of the molecule to be 2, i.e W=2. Hence, S=kln(2). Another approach is to calculate the work done by the molecule (isothermal expansion), which equals to kTln(2). Do you know that the Boltzmann equation is inscribed on Boltzmann's gravestone! Actually, it's not just Boltzmann, the Schrödinger equation is also inscribed on Schrödinger's gravestone.
:)
I searched for equations. You disappointed me. < :( | :P > But greatly done.
Hehe. Thanks, man. You already know what happens when we bombard the post with equations :D
Content type: Long, popular.




Awarded 4 out of 6 owls:
Details: The spelling and grammar owl was not awarded since there are a number of errors (First, Let's -> First, ... now. let's say ...-> now, Let's say , separated from each by -> separated from each other by, General Institution -> General Intuition (auto correct?) , an information -> information etc.). The originality owl was not awarded since it requires the science to be explained in a novel/creative way.
Whoa, the sexy science owl! I didn't get that last time. I need to work on my grammar skills. Thanks for pointing out the errors, I have made some corrections (only those which I could discern) :)
Just a keyword (that I gave to someone else too some time ago): Maxwell's zombies (this will be for your next post :D ).
Great post! :)
Thank you so much for taking the time to read and comment on my post :) Well, I haven't thought much about my next post but yeah, Maxwell's zombies is a great idea. Thanks again! :D
My pleasure. For some reason, it is the second time I mention this idea, but no one never wrote on it (or I just missed the post :p )
I learned about Maxwell's demon a few years back (Our physics professor made us write a paper on Maxwell's demon and information theory) but tbh this is the first time I am hearing the word "Maxwell's Zombie". I couldn't find anything about the term maxwell's zombies except for a short Wikipedia page. The wiki categorises Duncan's paradox as Maxwell's zombie. I know there are lots of challenges to the second law since it doesn't have any general proof. So, can all the challenges to the second law be called as maxwell's zombie?
(sorry for the late reply, i have been a bit busy this week) :)
I actually don't know much about them myself. Just that this exists. I have heard about them for the first time during a job interview, found the wikipedia page too, but never been further (time is what it is: not extendable).
The laws of thermodynamics are so interesting.. I remember taking thermodynamics in school. But your experiment or analysis on this law is awesome man.! It takes good understanding to write something like this.
Yes indeed the laws of thermodynamics are interesting and we get more interesting results when we try to violate them. Thank you so much,my fellow mechanical engineer :)
Information is physical. Never came across that in my life. You perfectly explained this that I find it literally so easy to understand. Looking forward to your next post man.
Job well done !
Thanks, buddy. Happy to see a biochemist appreciate my physics article ;)