Series: How did James Clerk Maxwell change our world? [ part 2: Beauty of the Maxwell's equations ]
In previous post part 1: Life and time I introduced the biography of James Clerk Maxwell, and that his classical theory of electromagnetism as presented in four sets of field equations underpins vastly many of our modern technological advances.
These equations paved way for all great accomplishments in telecommunications, electrical engineering and physics. This day, the relationship between electricity and magnetism, accompanied with the wave nature of light and electromagnetic radiation as a whole is encoded in the four Maxwell equations by Oliver Heaviside shown below in point form.
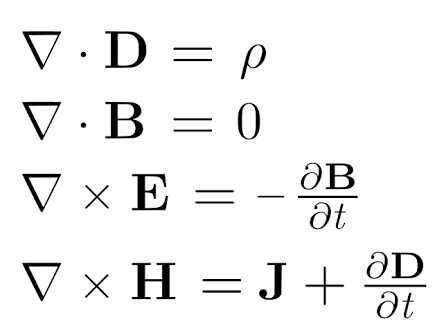Image credit: Wikimedia Commons, Figure Maxwell'sEquations by YassineMrabet CC BY 3.0
- The Four Governors
1. Gauss's Law for Electricity
∇• D =ϱ [Equation 1]
∇ - divergence operator
D - electric field displacement
ϱ - electric charge density
This is the first of Maxwell's equations which shows how the electric field behaves around electric charges. This equation is in point form that is it is true at any point in space. This means that if there exists electric charge somewhere, then the divergence of the Electric Flux Density "D" at that point is non zero, otherwise it is equal to zero. To have a broader understanding of Gauss's law, check Gauss's law in integral form.
• Significance of the Law
Gauss's Law for electricity states that the electric flux round a closed surface is proportional to the total charge enclosed within the surface. This means that electric charges act as sources or sinks for electric fields. The integral form of Gauss's laws is applied in calculating the electric field around a charged object. To show that this law is consistent with Coulomb's law, it is best practised to apply Gauss's law to the electric field of a point chargeLet's think of this using water analogy. As water flowing out of the end of a tube in a basin, if we enclose the source of water in any kind of surface the total amount of water flowing out through the surface will always be same regardless of whatever surface you put around it.
Image credit: Wikimedia Commons, Figure EM_dipoles by Maschen CC0 1.0
2. Gauss's Law for Magnetic Field
∇• B = 0 [Equation 2]
B - magnetic flux density
Comparing this Magnetism Law with the first law of electric fields, we can see that they are the same with the exception that the divergence of the Magnetic flux density is zero that is net flux through the surface is always zero (check integral form of this law for broader understanding).
We could as well have said that the divergence of B is equals to the "magnetic charge density", but this is not just the case as no one has ever found magnetic charge, not in a laboratory or anywhere. Thus, until this hypothetical magnetic charge is found, the right hand side of Gauss's Law for Magnetism is set to zero.
• Significance of the Law
Gauss's Law for Magnetic fields states that there are no existence of magnetic monopoles.That means the net magnetic flux bounded by any surface is zero. This law suggests that while we have found electric charges, we have never found the magnetic equivalent (magnetic charges or monopoles).3. Faraday's Law
Image credit: Wikimedia Commons, Figure Area_Faraday by Michael Lenz CC0 1.0
∇× E = - ∂B/∂t [Equation 3]
× - curl
This law dictates that an electric field will be created round a time varying magnetic field. It proves how we can use magnets to generate current, in devices such as dynamo and transformers in power station. Maxwell derived that perpendicular varying electric and magnetic field could form wave, and the outcome turned out to be very close to the speed of light. For the first time, light was hypothesized as an electromagnetic phenomena.
Significance of the Law
This law states that the line integral of the electric field round a closed path is equal to the negative of the rate of change of the magnetic flux through the area bounded by the path.It establishes that if an electric current results in magnetic fields, then a magnetic field can result in electric current.
4. Ampere's Law
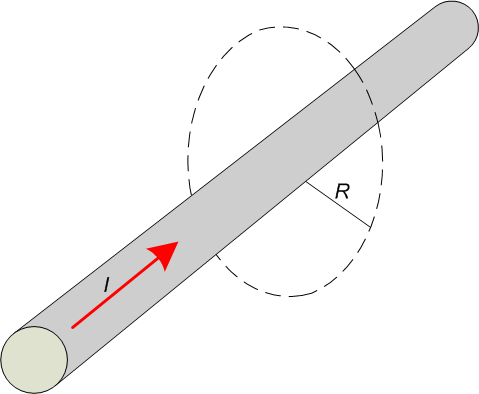.png)
Image credit: Wikimedia Commons, Figure Amper1 by RokasT CC BY 3.0
∇× H = J + ∂D/∂t [Equation 4]
H - magnetic field strength
J - conduction current density
D- electric displacement
This law renders how loops of magnetic field are formed by current or varying electric field through a loop. This depicts how to make electromagnets and calculate field strength in a solenoid.
• Significance of the Law
This law states that the line integral of the magnetic field around a closed path is equals to the total steady current passing through any surface bounded by that closed path. This renders that a flowing electric current results to a magnetic field that circles the current.Today we expanded and learned how James Clerk Maxwell changed the world with his powerful set of equations finding vast applications in physics, telecommunication and electrical engineering. Until next time, keep steemSTEM!
References & Further reading
IEEE Spectrum
For more scientific-related contents check #steemSTEM and #stemng. Follow at @steemSTEM and @stemng. Follow me if you like my posts and you want to read some more. If you have any thoughts/suggestions feel free to leave a comment!
This really brings back some memories.
I've always been fascinated by these laws but I always thought somebody should be able to explain them in absolute layman terms.
I think I understand some of the concepts but many parts of these equations are still very obscure to me.
To start with:
Sorry if all of these questions sound a bit lame but I feel like these equations are pivotal to so many applications I would love to truly understand them.
Maybe an idea for posts in the future would be to explain each equation, one at a time, for people with no or little backgrounds in mathematics/physics?
Thanks for all the hard work.
Wow. Loads of questions you got there. These laws are all embodiments of mathematics.
• Divergence in this context is a mathematical vector operator. Think of "divergence" this way : the measure of the amount of flow out of a specified volume minus the flow into that volume. That is "amount leaving" minus "amount entering" a given volume, the resultant is your divergence.
• Think of "Electric field displacement" this way:
Think of a these charges moving from point to point in a surface or field.
Their movement from point to point cover distances which is "displacement". The entities doing the movement are the charges. So we say electric field displacement that is charges per unit area that would be displaced(moved) across a layer of a conductor placed in an electric field(region where you have current flowing).
• YES! flux same analogy with water example you stated. this way electric field displacement is another way of saying electric flux density both having same symbol " D".
• Conduction current density; conduction current that is currents being conducted. Density; mass per volume.
So conduction current density is the amount of conducting current flowing on a surface( which definitely has a mass and volume) in a time.
• magnetic field intensity (H) is simply the strength of that magnetic field. Meaning how intense is the field?. While "J" is conduction current density not induction field.
Induction field: think of a generator engine. The cores where you have the magnets and coils. That's an induction field.
Trust this helps @irelandscape
I have the same thoughts too. Thank you for listing it.
OK, thanks for the explanations. I'll reread careful your post with that in mind when I have a chance.
BTW, I think there is potentially almost a lifetime of deeper understanding into these laws. I wonder how many trained people are out there who know these laws, can apply them but don't fully understand them.
@irelandspace, I think you replied the wrong person (me) :)
You are right @irelandscape. We just have to keep digging and learn more. Others take up from where others stopped. I believe no one knows it all.
Interesting read, if you could break it down into more straightforward article devoid of scary integral equations, it would be easier to grasp. Good effort here. Thank you.
Thanks.
our tutors did not break it down for us in layman's language. Na so we see am. Lol. Just for laughs😂
I guess you'd have to do better than that. We all attended the same standards of schools, but we try to learn more after school so that we can explain most complicated things in the easiest ways possible. Thank you.
Was kidding. I said "just for laugh".
Oh, it's all good then.
Being A SteemStem Member