EL PROBLEMA DEL ÁREA EN LA MATEMÁTICA GRIEGA (PARTE II)

La parte I de esta secuencia de posts nos dejó analizando cómo fue posible para los griegos, estudiar el asunto del área de las figuras planas sin disponer del concepto de número real, tan necesario para nosotros al abordar este mismo problema. El texto clave para esta interpretación es Elementos de Euclides, puesto que es la obra resumen de casi toda la matemática conocida hasta el momento de su redacción. El "casi" deja por fuera el tema de las cónicas, para el cual el propio Euclides escribió un tratado, hoy perdido. Por fortuna, poco tiempo después el gran geómetra Apolonio escribió su genial obra Cónicas, en la que recogió este conocimiento y añadió resultados de su propia cosecha.

Pero volvamos al área en Euclides y sus Elementos. Recordemos del post anterior que, desde la proposición I.4, el alejandrino usó el concepto de igualdad entre figuras con la idea de congruencia, pero las nociones comunes 2 y 3, le permitieron ampliar esta concepción hasta lo que hoy llamamos con rigurosidad figuras de igual área; Euclides simplemente diría figuras iguales. Podemos ver la aplicación de las nociones comunes 2 y 3 con un sentido lúdico, según el cual actuarían como criterios para mudar de sitio las piezas de un rompecabezas cambiándole la forma, pero manteniendo el área del mismo.

Todo este movimiento comienza en la proposición I.33. Según el historiador Proclo esta proposición es, al mismo tiempo, un cierre y una apertura: cierra la teoría de las paralelas iniciada en I.27 (donde se aplica por primera vez el famoso quinto postulado) y abre la teoría de los paralelogramos y su relación con los triángulos, es decir, la comparación de sus áreas. La proposición I.33 dice:

Las rectas que unen por (los extremos que están en) el mismo lado a (rectas) iguales y paralelas son también ellas mismas iguales y paralelas.

Estoy usando la traducción de M. L. Puertas C. para el teorema que hoy solemos enunciar en la forma: paralelas entre paralelas son iguales (por supuesto que hablamos de los segmentos incluidos entre las paralelas). Proposición con la que Euclides prácticamente define el término paralelogramo, siguiendo su línea teórica constructiva, según la cual un objeto no existe si no damos un procedimiento efectivo mediante el cual pueda construirse. Volvamos de nuevo a M. L. P. C. para revisar esta vez la proposición I.34:

En las áreas de paralelogramos los lados y los ángulos opuestos son iguales entre sí, y la diagonal las divide en dos partes iguales.

(Vale la pena comentar que M. L. P. C. usa la palabra diagonal donde otros traductores usan diámetro.)

Es muy rico el comentario de Proclo acerca de esta última proposición. De hecho, es la primera en la que el geómetra usa la palabra paralelogramo, mostrando además las tres propiedades que lo definen:

1. Igualdad de lados opuestos.
2. Igualdad de ángulos opuestos.
3. Igualdad de los triángulos definidos por cualquiera de las dos diagonales.

La demostración que hace Euclides aprovecha su teoría de las paralelas (igualdad de ángulos alternos internos) y la proposición I.33 para conducir hacia la proposición I.4 que -como comentamos en el post anterior- es nuestro actual postulado LAL de congruencia de triángulos; la presencia de los triángulos congruentes garantiza las tres igualdades comentadas.

Aparte de ello, nos convence Proclo de que la misma palabra paralelogramo proviene de la musa euclidiana; según él se la debemos al alejandrino, y con la cual quiso abarcar solo figuras cuadriláteras aunque hubiera podido incluir otras como, por ejemplo, el hexágono o el decágono regulares.

Caracterizados de esta manera los paralelogramos, procede el texto a mostrar sus propiedades de área. La proposición I.35 dice:

Los paralelogramos que están sobre la misma base y entre las mismas paralelas son iguales entre sí.

La lectura de la demostración, en la redacción arcaica del texto de los Elementos, oculta al lector moderno el sentido profundamente lúdico de la propia demostración. Se puede consultar a M. L. P. C. o a Heath, pero la ilustración que sigue fue elaborada según el principio lúdico comentado.

Son cuatro copias de la misma ilustración de Euclides. El autor se propone demostrar la igualdad de los paralelogramos ABGD y EBGZ, quienes comparten la base común BG y están entre las mismas paralelas. La primera copia es idéntica a la del texto. En la segunda y la tercera se destacan en amarillo dos triángulos (ABE y DGZ) de los que se demuestra (por teoría de paralelas) que son iguales (congruentes). Peros ambos tienen una zona común: el triángulo DEH, destacado en naranja en la cuarta copia. Al quitar este triángulo naranja a los dos triángulos amarillos lo que queda son los paralelogramos en estudio, que son iguales (tienen la misma área), por aplicación de la noción común 3, descrita en el post anterior. ¿No es como armar un rompecabezas? ¿Entiendes por qué hablo de lúdico? Pero sigamos con lo que sigue, es decir, vamos hacia la proposición I.36:

Los paralelogramos que están sobre bases iguales y entre las mismas paralelas son iguales entre sí.

Es una situación como la indicada en la figura anterior para los paralelogramos amarillos a la izquierda (ABGD y EZHT): no comparten la base, pero están entre las mismas paralelas y sus bases (BG y ZH) son iguales entre sí. La demostración es harto sencilla, pues basta con conseguir un tercer paralelogramo (el anaranjado EBGT) que comparte base con cada uno de los dos separados y está entre las mismas paralelas. En este caso, Euclides hace uso de la noción común 1:

Las cosas iguales a una misma cosa son también iguales entre sí

Le toca ahora el turno a los triángulos. Las dos proposiciones anteriores pueden parafrasearse idénticamente cambiando paralelogramos por triángulos. Es el contenido de las proposiciones I.37 y I.38:

Los triángulos que están sobre la misma base y entre las mismas paralelas son iguales entre sí.

Los triángulos que están sobre bases iguales y entre las mismas paralelas son iguales entre sí.>

La primera

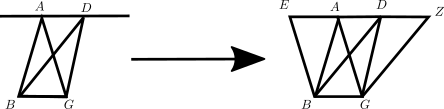
convierte la figura de la izquierda en la de la derecha, es decir, de cada triángulo produce un paralelogramo simplemente desplazando uno de los lados del triángulo paralelo a sí mismo hasta llegar al vértice opuesto. Por ejemplo del triángulo AGB se obtiene el paralelogramo AGBE, por desplazamiento del lado AG hasta BE. Al tener los paralelogramos, aplica la proposición I.35. La I.38 procede de manera similar, reduciendo el caso a la I.36, con un diagrama como el siguiente:

Con las proposiciones I.39 y I.40 se acaban los rompecabezas y comienza una matemática de algo más de exigencia, pues es la hora de las proposiciones recíprocas:

Los triángulos iguales que están sobre la misma base y en el mismo lado, están también entre las mismas paralelas.

Los triángulos iguales que están sobre bases iguales en el mismo lado, están también sobre las mismas paralelas.

Las proposiciones recíprocas exigen una herramienta de alta estimación para el matemático griego: la reducción al absurdo. Por ejemplo, la primera de las dos anteriores, usa la siguiente figura:

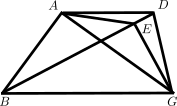
en la que los triángulos de la hipótesis son ABG y DBG, supuestos iguales por hipótesis, sobre la misma base BG y cuyos terceros vertices están del mismo lado de dicha base. La demostración supone que la recta AD no es paralela a BG y marca el punto E donde la paralela (supuesta) corta a BD. Al aplicar I.35, los triángulos ABG y EBG resultan iguales; por esta razón la hipótesis hace que EBG y DBG sean iguales, cosa contradictoria pues al ser el primero interior al segundo es menor. Para la demostración de I.40 te invito, lector, a que intentes tú mismo el diagrama antes de revisar el texto de Euclides.

Las proposiciones I.41 y I.42 establecen la relación específica entre paralelogramos y triángulos. La primera dice:

Si un paralelogramo tiene la misma base que un triángulo y está entre las mismas paralelas, el paralelogramo es el doble del triángulo.

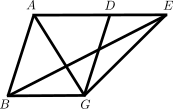
Para la demostración se comparan el paralelogramo ABGD y el triángulo EBG, que comparten la base BG. La solución la da la recta auxiliar AG, diagonal (diámetro) del paralelogramo que produce el triángulo ABG, quien comparte base con EBG y está entre las mismas paralelas. Son iguales por I.37, pero ABG es la mitad del paralelogramo ABGD.

La proposición I.42 es un problema:

Construir en un ángulo rectilíneo dado un paralelogramo igual a un triángulo dado.

Esta es la primera construcción de área en todo el tratado. Precisamente la carencia del concepto de número real, obligaba a que estos problemas se plantearan en términos de comparación de figuras. La figura más usada para comparación fue el cuadrado, razón por la cual aun hoy al problema de conseguir el área de una figura plana se le llama cuadratura. El enunciado de I.41 establece que el triángulo es la mitad del paralelogramo que tiene su misma base y altura, resultado que a posteriori resumirían las fórmulas

Ahora bien, I.42 plantea no solo la construcción del paralelogramo que tenga igual área que un triángulo dado; exige, además, que en el paralelogramo los lados estén inclinados según un ángulo también dado. La ilustración para la demostración es esta:

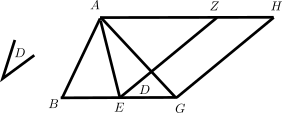
en la que el triángulo dado es ABG y el ángulo D. La solución se consigue trazando la recta AE, del vértice al punto medio E de la base BG. Esa recta divide al triángulo en dos triángulos iguales (¿por qué?). En el punto E se copia el ángulo D sobre la recta EG y su otro lado se prolonga hasta Z en la paralela AZ. Desde el vértice G se traza la paralela GH a EZ, hasta encontrar la prolongación de la recta AZ en H. Pues bien: ZEGH es el paralelogramo buscado. (Acá también, lector, debes contestar por qué. O si prefieres lo lees en el propio texto de Euclides, quien no deja afirmación sin justificación.)

En cuanto a los objetivos de este post, el cierre lo representa la proposición I.43:

En todo paralelogramo los complementos de los paralelogramos situados en torno a la diagonal son iguales entre sí.

Obligados estamos entonces (Euclides no lo hace) a explicar qué son los complementos. Tomemos para ello una réplica de la figura usada por el alejandrino para demostrar la proposición:

El paralelogramo de la hipótesis es ABGD y trazamos su diagonal AG. Por un punto K cualquiera de ella, tomado como referencia, trazamos dos rectas paralelas a las bases del paralelogramo: EZ y TH. Esa construcción produce la figura en escuadra que hemos coloreado en la réplica izquierda; a esa figura completa la llamará posteriormente gnomon y será un elemento importante a la hora de demostrar algunas proposiciones del libro II. La esquina superior del gnomon contiene un paralelogramo semejante al paralelogramo original (AEKT), que representamos en anaranjado; los dos paralelogramos en amarillo son los llamados complementos y son los objetivos de la proposición: debemos demostrar que son iguales entre sí.

Para la demostración nos ayudamos con la segunda réplica a la derecha. En ella destacamos en naranja los dos paralelogramos internos semejantes al paralelogramo original. Ambos son cortados por la diagonal en dos partes iguales. Eso es suficiente para hacer la demostración, apoyados en las nociones comunes. Pero yo voy a seguir el ejemplo de Descartes y no te voy a privar, lector, del placer de que completes los detalles tú mismo o, en su defecto, los leas directamente de la obra original.

REFERENCIAS

1. Euclid. The thirteen books of the Elements. (Translated with introduction and commentary by Sir Thomas L. Heath. 3 volumes.) Edit. Dover. New York. 1956.

2. Euclides. Elementos. Traducción y notas de Marı́a Luisa Puertas Castaños. Edit. Gredos, Madrid, 1991. (Tres volúmenes).

3. Douglas Jiménez. El problema del área en los Elementos de Euclides. Boletín de la Asociación Matemática Venezolana, Vol. XVII, No. 2 (2010). Págs. 179-207.

4. Douglas Jiménez. Historia de la matemática: Pitágoras y el pitagorismo. CreateSpace.com. 2013.

5. Proclus. A commentary on the First Book of Euclid's Elements. (Translated with Introduction and notes, by Glenn R. Morrow). Princeton University Press. New Jersey. 1970.

Notas aclaratorias. Las ilustraciones de este post fueron realizadas por mí, usando el programa de software libre Inkscape. Voy a hacer promoción de estas entradas por mi twitter de Historia de la Matemática, @HistoMat. Mi twitter personal (para cosas distintas a HM) es @dougjimenez.

Nota de disculpa. Aun queda material para varias entregas más en este tema, pero voy a estar algunos días fuera de circulación. Me esperan, no se vayan a ir.

Nota de protesta. Continúo en mi insistencia de que los desarrolladores de steemit, incluyan en el front end las facilidades de markdown para el uso de LaTeX. Eso nos aliviará muchísimo la vida a quienes queremos escribir matemática en esta red.