Ancient Knowledge: How did the Romans do math?
Ancient Knowledge: How did the Romans do math?
Maybe for many, as for me, it is very interesting to know how ancient civilizations worked, that is why today while I was reading an article about the Roman Empire and its incredible power and scientific advances, I could not help but wonder, how could that great civilization did the mathematical calculations ?.
For many, it will be more than obvious that the simplest answer would be to say that they used an abacus. And they are right that was the fundamental tool for calculations ... But beyond the abacus, the Romans also made manual calculations. Calculations that were not easy to perform by Roman numerals, compared to Arabic numerals that were simpler for the time.
That's why today I wanted to change a bit the subject of my post (which usually revolve around chemistry) and give an explanation as clear as possible of how these complex operations were carried out
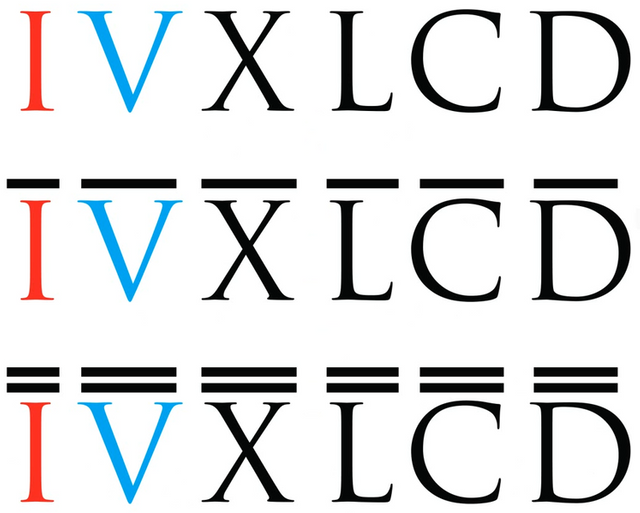
Source
CC BY-SA 4.0
The Roman numeral system.
Assuming we all know the Roman numeral system, I will explain something about it. The Roman numeral system is basically a non-positional mathematical system since it establishes values for certain letters.
As we can see in the first image, at the time the Romans did not have symbols with which to symbolize quantities greater than 1000, although some modern alterations add a bar on top of each of the letters to symbolize the product of its value per thousand. That is to say, that for example the letter V whose value is 5 when adding the top bar its value would become 5000 thus progressively with the other letters.
It should be noted and as many will know that the interpretation of these numbers goes beyond just being represented by letters and is that another curious aspect of this numbering is that if we write a symbol before another with a higher numerical value we will be subtracting the minor to the greater.
While on the other hand, if we place the highest value back, we will be adding the lowest to the highest.
In general, the writing of a number in this system is designed around the larger symbol used to write the number.
Sum of Roman numbers.
This is when the thing starts to get a bit complex. Since to sum with Roman numbers, it is necessary to follow the following rules:
We transform subtractions into sums. For example, IX should be rewritten as VIIII (even if the I cannot be replicated more than 3 times).
We group the two numbers that we want to add.
We rearrange the letters (numbers) in decreasing order according to their value.
We do internal sums from right to left. For example, if IIIII appears, we replace it with V.
We return to transform the subtractions in the places where necessary to comply with the rules of writing.
Let's see an example: 145 + 79. In Roman numbers, it would be written: CXLV + LXXIX.
CXLV becomes in accordance with the rule of the sum in CXXXXV and LXXIX becomes LXXVIIII
Then we order both terms in one CXXXXVLXXVIIII
We rearrange in decreasing order CLXXXXXXVVIIII
We add the similar terms to replace them with higher terms, VV becomes X. Remaining CLXXXXXXXIIII. Then the XXXXXXX is replaced by LXX. In this way, CLLXXIIII remains. And finally, the LL terms become C. Finally, CCXXIIII remains.
Finally we place subtractions where they correspond so we change IIII with IV. So that we have the final result, that is: CCXXIV = 224.
Subtraction of Roman numerals.
Making subtractions with Roman numerals is a little less complicated, and you should only follow these steps:
First we transform the subtractions into sums.
Then we proceed to eliminate the common symbols between both figures.
Then we take the largest symbol that remains in B to rewrite it in the first symbol of A larger than it so that there are similarities of symbols in both figures A and B. In order to apply the step described above.
Reorder the symbols and convert them into subtractions where necessary.
Let's see an example: 241 - 85. In Roman numerals: CCXLI - LXXXV
First CCXLI becomes CCXXXXI. While LXXXV remains the same.
We eliminate XXX from each of the figures. Remaining CCXI and LV
Then the most complicated step, as L is the major symbol of the second figure we rewrite a C of the first as LXXXXX. Thus, CLXXXXXXI and LV remain. We eliminate both L of the two terms to obtain thus; CXXXXXXI and V. Then we repeat the step we took with L and since V is the only symbol that remains in the second term, we rewrite a X of the first term based on V as VIIIII. In order to obtain CXXXXXVIIIIII and V. We eliminate the V of the two terms and we have CXXXXXIIIIII. Finally, we rearrange again according to the writing rules so that CLVI remains
Ready the final result is CLVI = 156.
Multiplication of Roman numerals.
I have to say that this is when things start to get really confusing and complicated since there is no easy or simple way to do it. Perhaps many will be thinking that the most efficient solution would be to make many successive sums but they are wrong is not the most convenient.
In order to solve A x B we make two columns and place A on the one on the left and B on the one on the right. Then we execute these steps:
Divide A by 2 and place the result of the division below A. For example, if A is 15 we will put down 7 (without decimals of course)
While in B we do the opposite and multiply it by 2. And also placed the result below.
We repeat the previous steps with the results that we are getting until in the left column there is a 1.
Remove from both tables all the rows in which the number on the left is even.
Then we proceed to sum the numbers that we have obtained in the column on the right, that is B. The result of this sum is the result of A x B.
Let's go with an example. We are going to do 45 x 29. In Roman numerals XLV x XXIX. We made the table and executed the first 3 steps.

Table made by me
@josalarcon2
Then we eliminate the rows where the number on the left is even. The table is as follows.
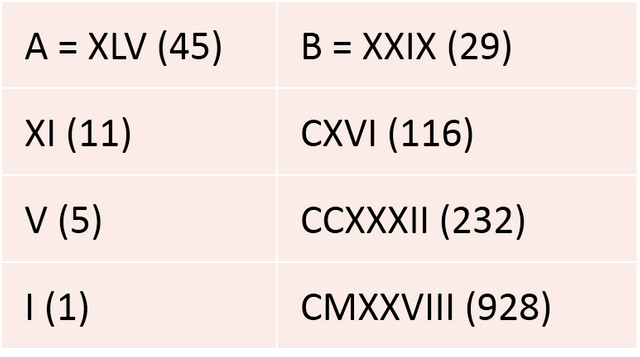
Table made by me
@josalarcon2
Finally, we will sum the numbers that we have obtained in the column of the right:
XXIX + CXVI + CCXXXII + CMXXVIII =
= XXVIIII + CXVI + CCXXXII + DCCCCXXVIII =
= [We group and reorder from highest to lowest value] =
= DCCCCCCCXXXXXXXXVVVIIIIIIIIII =
= DCCCCCCCXXXXXXXXVVVVV =
= DCCCCCCCXXXXXXXXXXV =
= DCCCCCCCCV =
= DDCCCV =
= MCCCV
And in that way, we will obtain the result we were looking for
MCCCV = 1305
Division of Roman numerals.
The last of the operations and without a doubt the most confusing and problematic, since for this operation I can not achieve general rules that allow us to solve it in the simplest way possible. So all we can do is subtract the divisor from the dividend until we get a result less than the divisor.
The number of times we have to subtract will be the quotient of the division. For example, for 23 between 5 would be:
Another alternative would be to find some common factor for the two numbers that we wish to divide. Thus, before making the division, we can simplify the two numbers per disk factor and the operations will be easier since we would be operating with smaller numbers. But anyway it's still very annoying.
Conclusion.
As you have been able to realize if you read the post carefully, what I said at the beginning is true, perform operations with the Roman numerical system is extremely complicated and border on the annoying. However, as I described them, there are certain rules and steps that make the task of solving some operation under this numerical system more digestible.
However, despite these rules, handling very high numbers implies a task that can take a long time, and without taking into account that in the case of divisions there is no rule that I could achieve.
Finally, I hope you liked my explanation, even though it is something that little by little is becoming totally useless to know but that still generates a lot of intrigue in people like me.
References.
SteemSTEM
SteemSTEM is a community-driven project that now runs on Steemit for more than a year. We seek to build a community of science lovers on Steemit and to promote well written/informative Science Technology Engineering and Mathematics (STEM) postings in order to make Steemit a place for fascinating STEM content.
So if you want to read more scientific articles of good quality, visit the hashtag #steemstem and scienceON.

Disclaimer:
[1] All the content exposed in this post is a compilation of different sources besides my knowledge in the subject.
[2] All the images used are correctly labeled for reuse.
)
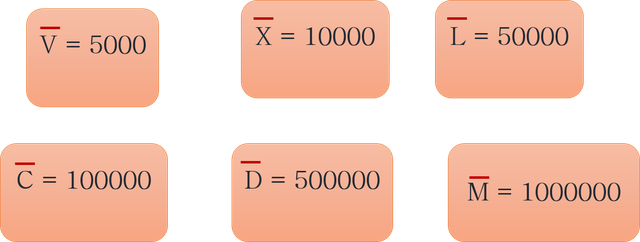)
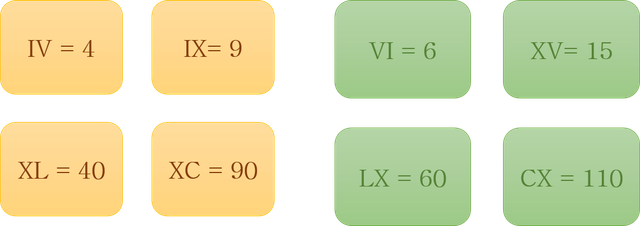
)
Given the amount of engineering left by the Romans, it is, indeed, astonishing how little pure mathematics survives. One clue can be gleaned from Vitruvius, who says that all "tricky" problems were solved geometrically.
Perhaps the fall of the roman empire was because no one could calculate with large numbers :)
😄
Interesting, clear, and nicely illustrated.
I liked the ingeniousness of the multiplication procedure, though no doubt laborious. I'm glad I wasn't a student back then!
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by josalarcon2 from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Lol... The roman numeral. This thing used to confuse me quite a lot in my elementary education. I find it interesting now.
I studied the classics at university and I just want to say great work. It was very interesting and informative.
Thanks. I'm glad you like it
Your Post Has Been Featured on @Resteemable!
Feature any Steemit post using resteemit.com!
How It Works:
1. Take Any Steemit URL
2. Erase
https://3. Type
reGet Featured Instantly & Featured Posts are voted every 2.4hrs
Join the Curation Team Here | Vote Resteemable for Witness
I'm risking to be recognized as some spammer, but seriously:
great post and thanks for sharing.
Poor Romans, this wasn't practical at all, but once you get familiar with it and develop the routines, I guess it becomes fine.
No sé si es cierto q nosotros lo tenemos mejor,lo q si se es que ejercitaban su cerebro al máximo