Alternating equations to the ideal gas state equation.
The ideal gas state equation is very simple, but its scope of applicability is very limited. It is desirable to have state equations that represent accurately and without limitations the P-v-T behavior of the substances in a larger region. Naturally, this class of equations is more complicated. For this purpose, several equations are known, but in this opportunity, we will study only three of them, which in my opinion are the most important. These are the following:
Van der Waals state equation.
The Van der Waals state equation was proposed in 1873, it has two constants that are determined from the behavior of a substance at the critical point, and is given by:
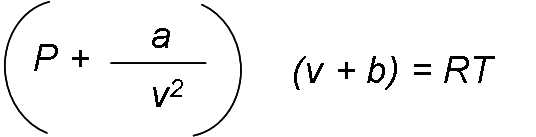
Van der Waals tried to improve the ideal gas state equation by including two of the effects not considered in the ideal gas model: the intermolecular attractive forces and the volume that the molecules occupy by themselves. The term a / v2 takes into account the intermolecular forces and b the volume occupied by the gas molecules. In a room at atmospheric pressure and temperature, the volume that actually occupies the molecules is about one-thousandth of the volume of the room. As the pressure increases, the volume occupied by the molecules becomes an increasingly important part of the total volume. Van der Waals proposed to correct this by replacing v in the ratio of the ideal gas with v - b, where b represents the volume occupied by the gas molecules per unit mass.
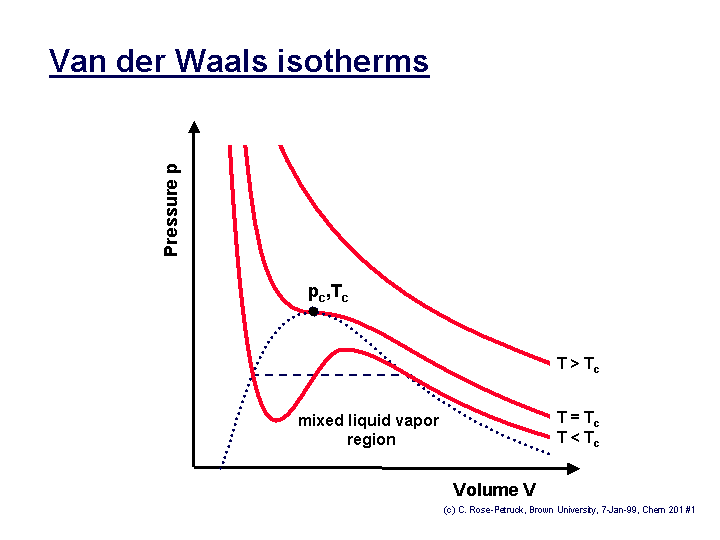
The determination of the two constants that appear in this equation is based on the observation that the critical isotherm of a P-v diagram has a horizontal inflection point at the critical point.
Source
Thus, the first and second derivatives of P with respect to v at the critical point must be zero, that is:
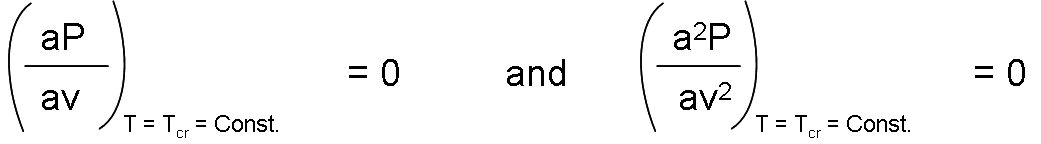
When carrying out the derivatives and eliminate v (cr), constants a and b are obtained.
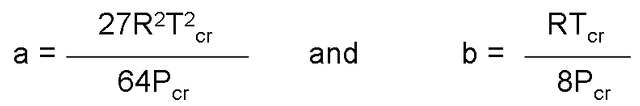
For any substance, the constants a and b are determined only from the data of the critical point.
The accuracy of the Van der Waals state equation is often inadequate, but it can be improved by using values of a and b based on the actual behavior of the gas over a wider range, rather than a single point. Despite its limitations, the Van der Waals state equation has a great historical value because it represents one of the first attempts to model the behavior of real gases.
Beattie-Bridgeman's equation of state.
The Beattie-Bridgeman equation of state, proposed in 1928, is a state equation based on five constants determined experimentally. It is expressed as:
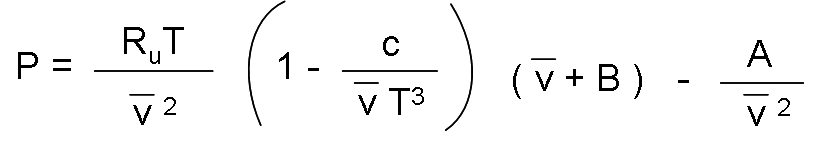
Where:
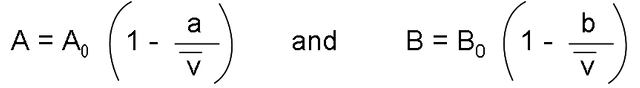
The constants that appear in the above equation are offered for several substances in the following table:
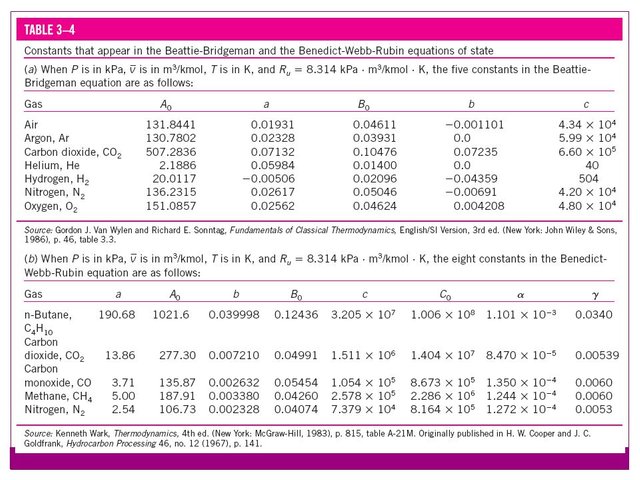
Source
State equation of Benedict-Webb-Rubin.
In 1940, Benedict, Webb and Rubin extended the Beattie-Bridgeman equation and managed to increase the number of constants to eight. It is expressed as:
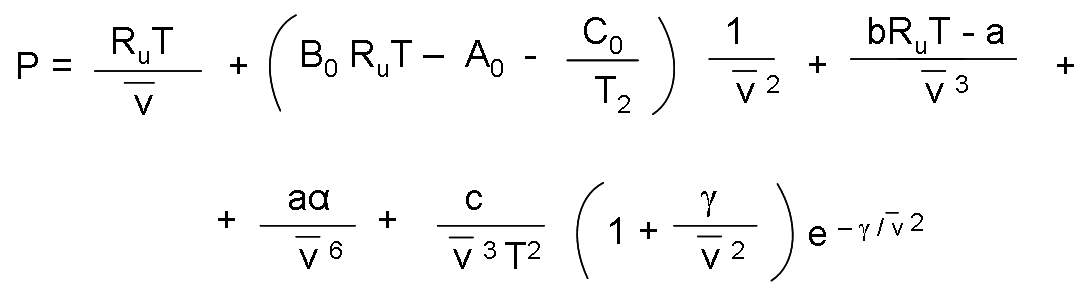
The values of the constants that appear in this equation appear in the table previously presented.
In 1962, Strobridge further expanded this equation by increasing the number of constants to 16.
References:
- Thermodynamics: An Engineering Approach Sixth Edition, by Yunus A. Cengel and Michael A. Boles.
- Application of the Benedict-Webb-Rubin equation of state to argon, by David Zudkevitch and Thomas G. Kaufmann.
- http://www.sparknotes.com/chemistry/gases/real/section1/
- http://www.ccl.net/cca/documents/dyoung/topics-orig/eq_state.html
- http://machineryequipmentonline.com/hydraulics-and-pneumatics/properties-of-pure-substancesother-equations-of-state/
- https://getmyuni.azureedge.net/assets/main/study-material/notes/mechanical_engineering_engineering-thermodynamics_properties-of-pure-substances_notes.pdf
