Part II Gravitational field
3- Law of universal Gravitation
As we have seen, two bodies placed in presence of one another exert a force of attraction between them. This property is revealed by the Cavendish twisting balance, built for this purpose; however, for moderate bodies of mass it acquires very small values.
This scale consists of two spheres ordinarily gold or platinum of known mass, mounted on a light horizontal bar, which is suspended by its center of a quartz thread. By means of a mirror fixed to the thread, the light of a light beam is reflected on a scale. Two large masses of lead are arranged as indicated in the figure below and it is observed that due to the force of attraction in the masses of the system a pair of forces originates, which sets the balance in motion. This movement is recorded by the deviation of the light beam on the scale.
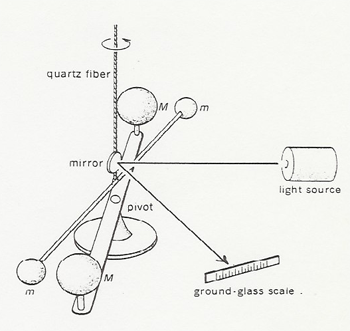
Source
Newton concretized this phenomenon with the law of universal attraction, which bears his name: "Between any two bodies of the Universe, of masses m and m', there is a force of attraction that is directly proportional to the product of said masses and inversely proportional to the square of the distance that separates them. "The mathematical expression of this law is:
(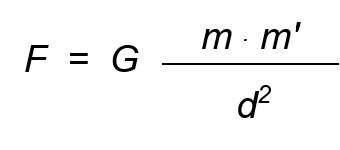 )
)
The value of this force is independent of the size and shape of the body. The distance d of the formula is taken between the centers of gravity of both bodies. Due to the extraordinarily small value of G, the forces of attraction between bodies are of little value, except when their masses - or at least one of them - reach a considerable value.
4- Weights of the bodies
It was previously indicated that the value of the force of attraction between bodies is small and hardly appreciable between currents. Now, if one considers the reciprocal action between the mass of a body and the mass of the Earth, it follows that the force now acquires considerable value, known as the weight. Thus, the magnitude of weight is a consequence of Newton's law of universal attraction.
«Weight of a body is the force of attraction that the mass of the Earth exerts on the mass of that one.»
If the mass of a body is m and that of the Earth M and the distance of the body to the center of the Earth d its weight will be given by the formula:
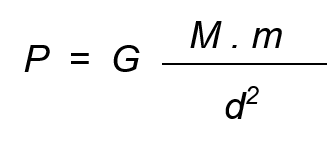
The weight of every body will be determined, therefore, by Newton's formula.
We must remember here that the mass depends only on the amount of matter that the body contains, regardless of where it is considered; instead, the weight of a body depends, in addition, on the distance it is from the center of the Earth.
As is known, the Earth prints to all the bodies that fall on it an acceleration:
g = 9.8 m / s2
We will see, now, how the value of g can be obtained from the law of universal gravitation.
For this, it is considered a body of mass m that is on the earth's surface. As the acceleration that would acquire in its fall would be g, the force exerted by the Earth -that is, the weight of the body- will be obtained by the formula:
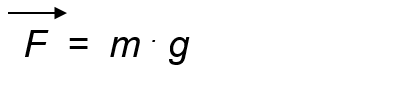
Independently, we will have the law of universal gravitation, which adapted to the gravitational field of the earth is:
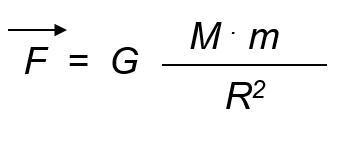
where: F(arrow) is the force of attraction; G, the factor whose value has been expressed previously; M, the mass of the Earth; m, the mass of the body, and R, the distance that separates the body from the Earth, distance that -because the body is on the earth's surface- is equal to the terrestrial radius.
Equaling the two expressions of F, we have:
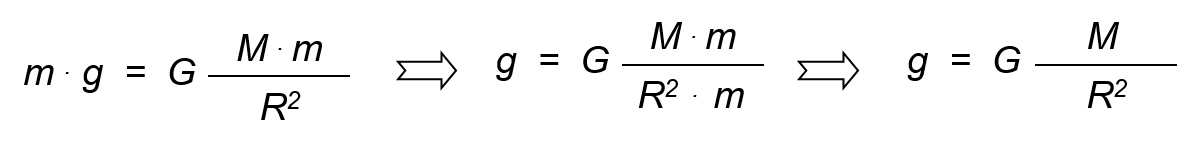
Substituting in this last expression the values:
G = 6,67 . 10-11 N . m2/kg2, M = 5,98 . 1024 kg R = 6,38 . 106 m
All of them expressed in units of the international system results:
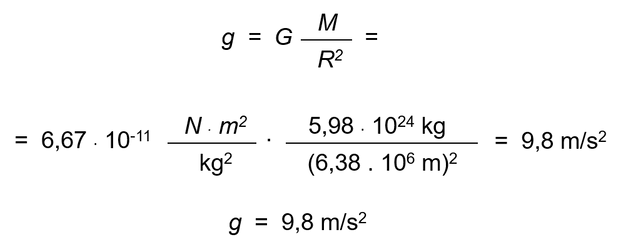
5- Intensity of the terrestrial gravitational field
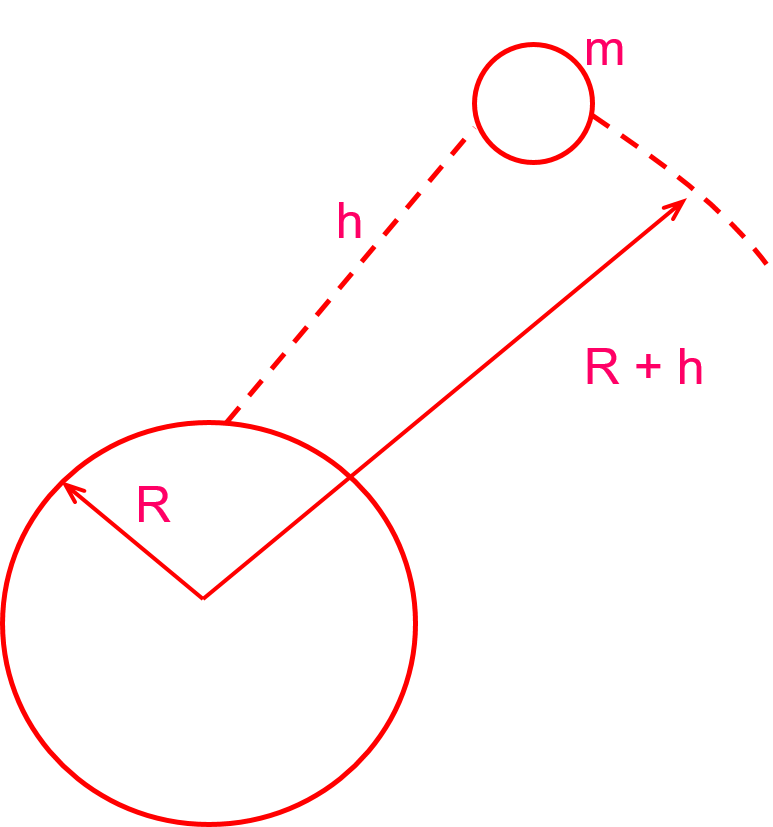
It is considered a body of mass m, which is at a height h above the earth's surface.
In these conditions, the distance from the mass m to the center of the earth is:
d = R + h
so, applying the law of universal gravitation. Said mass would be attracted by the Earth with a force:
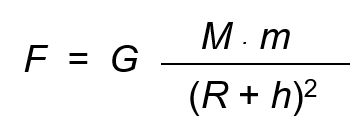
On the other hand, considering that the intensity of a gravitational field is the force exerted by it on the unit of mass, it can be expressed:
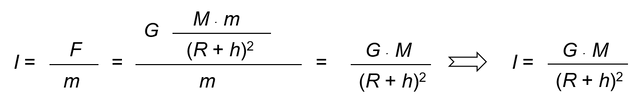
However,
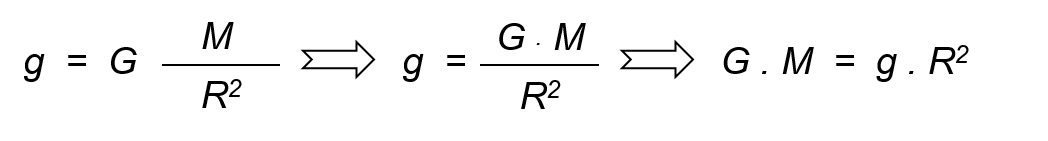
Substituting this value in the expression obtained above:
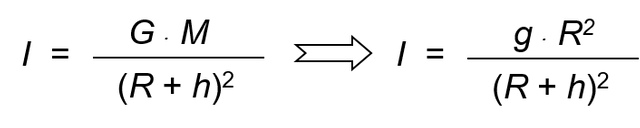
is obtained:
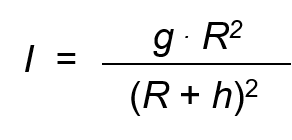
As can be seen, as h increases, the value of the intensity decreases, verifying that we are on the earth's surface:
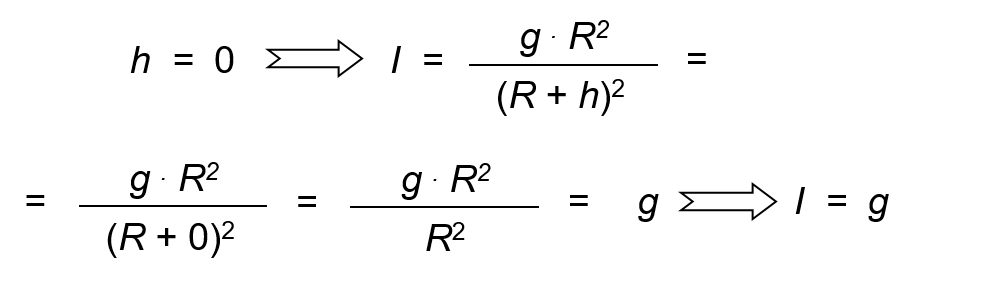
Consequently, it can be stated: "The intensity of the Earth's gravitational field, on the surface of the Earth, is equal to the acceleration of gravity."
For more information visit the following links.
- http://www.physicsclassroom.com/class/circles/Lesson-3/Newton-s-Law-of-Universal-Gravitation
- http://www.physics.louisville.edu/cldavis/phys298/notes/wgt_fbdiag.html
- https://hemantmore.org/physics-1/p11202009/3964/
- https://en.wikipedia.org/wiki/Cavendish_experiment
very interesting, I like this kind of topics. Basic, but important.