The famous Monty Hall paradox

Hi, I am new to this platform so feedback is always welcome

Introduction

Imagine you are in a game show called "Let's make a deal" on television with the chance to win a brand new sports car. The car is behind one of the 3 doors, behind the other 2 doors are goats (or donkeys). After you chose your door the game master (Monty Hall, who knows the location of the car) opens one of the 2 other doors with a goat behind it. Do you stick with the door your first choice, or do you switch to the other one? Does it even matter?

Image source

What you should do

At the beginning there is a 1/3 chance the car is behind the door. But whenever the game master reveals a door with a goat behind the odds change. It is not a 1/3 and 1/3 chance nor a 1/2 and 1/2 chance, but a 1/3 and 2/3 chance of winning the car.  Whenever the game master opens a door with a goat, he adds critical value. The initial door you chose still has a probability of 1/3 but the other door you didnt choose now has a probability of 2/3 (because the other unchosen door has definitely a goat). The pictures below explain this. 

Image source

Image source

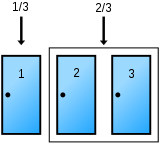
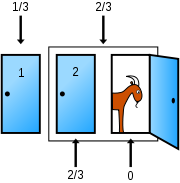
Another way of visualising this is trough a probability diagram. 

Image source

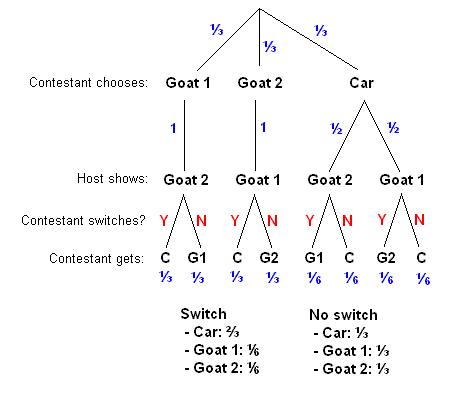
Surprisingl, you should always switch doors since this increase your chance of winning. The odds aren't 50-50, if you switch you'll have a chance of 2/3 to win the car. At first sight this seems absurd, this is why the problem became a paradox.

If you want you test it here

Sources

https://betterexplained.com/articles/understanding-the-monty-hall-problem/

https://en.wikipedia.org/wiki/Monty_Hall_problem

http://mathworld.wolfram.com/MontyHallProblem.html