Geometría analítica y Cinemática (Parte XVI)

En primer lugar mi saludo respetuoso para toda la comunidad académica y científica de steemit, en especial a #stem-espanol, #steemstem, #utopian-io, #curie, #cervantes y #entropia, gracias a su valioso apoyo hacemos posible nuestro crecimiento en todos los aspectos relacionados a esta prestigiosa plataforma y además nos permiten destacar la excelsa labor de la ciencia ya que por lo general nos olvidamos de su incalculable valor para la existencia de la humanidad.

Seguimos con la extraordinaria temática geometría, aquella que unida al imponente lenguaje abstracto del álgebra fortalecen el imprescindible carácter analítico de las matemáticas, característica fundamental implementada para el análisis del esencial nexo entre la majestuosa ciencia física y las indispensables matemáticas. Con La geometría analítica y la cinemática el campo de la ciencia ha logrado estructural todas aquellas herramientas necesarias para la comprensión sobre cualquier tipo de fenómeno de movilidad que se desarrolle en nuestro maravilloso universo y así lo hemos podido comprobar en cada una de las anteriores publicaciones.

De manera general la comprensión sobre cualquier tipo de movimiento será de vital importancia para la humanidad y eso ha sido nuestro principal propósito poder dar a conocer diferentes tipos de movimientos que forman parte de nuestro entorno y en consecuencia de nuestra cotidianidad, en donde nos hemos encontrado movimientos tales como; el circular, movimiento parabólico, elíptico, hiperbólico, rectilíneo-curvilíneo, oscilatorio, vibratorio, ondulatorio, caótico, armónico complejo, armónico forzado amortiguado, movimiento cicloidal, movimiento epicicloidal, hipocicloidal, movimiento cisoidal, encontrándonos también otros movimientos intrínsecos tales como el movimiento periódico el cual a su vez se considera un esencial aspecto del extraordinario movimiento armónico simple (M.A.S.), representando este último un fundamental modelo entre los fenómenos oscilatorios, resaltando siempre que cualquier partícula, cuerpo u objeto al desarrollar tales cambios de posiciones lo realizaran a través del lugar geométrico de cualquier forma o figura fundada e interpretada por el excelente lenguaje abstracto que implementa la geometría analítica.

Continuamos con el manejo de la grandiosa figura de la circunferencia y la esencial línea recta para seguir estructurando otras importantes curvas las cuales nos permiten hacer volar nuestra imaginación en cuanto a la manera de utilizarlas en nuestras vidas, por lo que hermosas y maravillosas curvas hacen posible la extraordinaria movilidad de cualquier partícula, cuerpo u objeto, por lo tanto podemos expresar que partiendo de la generación de una determinada curva obtendríamos la trayectoria de un particular movimiento como se ha comprobado anteriormente.

Tanto nuestros ojos como nuestra imaginación se asocian para fabricar una forma o figura geométrica al observar nuestro esplendido entorno y de esa forma es que la ciencia nos ha enseñado extrayendo de la naturaleza cualquier tipo de conocimiento con el firme propósito de aplicarlo en cualquiera de nuestras tareas o actividades a realizar, en donde una de las más notables aplicaciones podríamos decir que se encuentra en el mundo de la mecánica a través de la geometría cinemática y en consecuencia de la geometría dinámica, lo cierto es que esta parte de la ciencia (geometría cinemática) se ha convertido en una poderosa herramienta tanto para facilitar la comprensión durante la generación del lugar geométrico de una determinada curva por cualquier estudiante o persona particular, así como para la elaboración de grandiosos sistemas físicos con mecanismos articulados permitiendo optimizar tanto un determinado aprendizaje como el desarrollo de nuestras actividades habituales.

Por lo tanto, podríamos afirmar que gracias a la geometría analítica cinemática es posible poder detallar el lugar geométrico de una curva mientras la vamos estructurando debido a que siempre dependerá la estructuración de esa curva de un tipo de movimiento de un punto perteneciente a un plano, en donde el mencionado punto deberá cumplir con ciertas especificaciones o condiciones (aspecto analítico), y esto le permitirá dibujar el lugar geométrico definido para una determinada curva, convirtiéndose dicho lugar geométrico en la huella dejada por el punto en movimiento y por tanto en la trayectoria tanto para el punto que dejó sus huellas como para un particular movimiento el cual podría llevar cualquier partícula, cuerpo u objeto al transitar por la misma.

Según lo antes planteado es que podemos seguir confirmando que la cinemática se basa en el nombre de un determinado movimiento debido a que una partícula, cuerpo u objeto pudiera comportarse como lo hace el punto generador de una particular curva, en pocas palabras podemos atribuirle a un determinado móvil las características de movilidad similar a las implementadas por un punto al generar una curva y por tanto el movimiento llevado por tal móvil se relacionará con la trayectoria seguida por el mismo, por ejemplo un móvil que transita por una trayectoria recta desarrollará un movimiento rectilíneo tal y como lo realizó el punto generador de la línea recta y así respectivamente para los otras formas de movimientos, es decir, el móvil cambiaría de posición tal y como lo hace geométricamente un punto cualesquiera del plano cuando genera cualquier forma o figura como las curvas.

Resaltando la importancia de la circunferencia para la generación de otras curvas y en consecuencias particulares o compuestos movimientos podemos decir que a la misma la hicimos rodar sobre una línea recta originando a las curvas cicloidales y todas sus impresionantes características, para luego hacerla rodar, sin deslizarse, sobre otra circunferencia generando a las curvas epicicloidales, luego la rodamos o giramos por el interior de otra circunferencia y obtuvimos a las curvas hipocicloidales, después para la conformación de las curvas cisoides nuevamente nos apoyamos en la circunferencia pero para esa ocasión de forma estática o inmóvil y además con la ayuda de una línea recta la cual era tangente al diámetro de la misma por cualquiera de sus extremos y siguiendo ciertas condiciones logramos establecer el lugar geométrico para la cisoide de manera general.

Para este caso consideraremos a una circunferencia igualmente inmóvil con centro (C) y cuyo radio sea el segmento CA, en donde trazaremos por el centro (C) una recta determinada por KL y que la misma forme un ángulo β con el radio CA, ubicamos entre el arco formado entre los puntos A y K1 el punto D y desde este punto trazamos una recta o segmento hasta el origen del plano (O), es decir, OD esta recta de condición variable, de esta recta OD adquirimos un segmento ON el cual será igual al segmento ED, por tanto cuando la recta OD varíe el punto N tomará distintas posiciones representando de esta manera la huella o marca para el lugar geométrico de la curva denominada estrofoide, en donde, si el ángulo β = 90° dicha curva será una estrofoide recta y distinto a esto decimos que la estrofoide será oblicua.

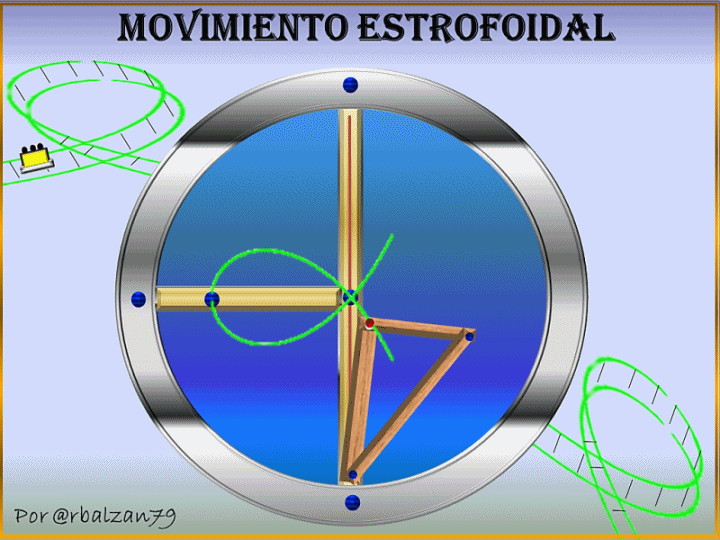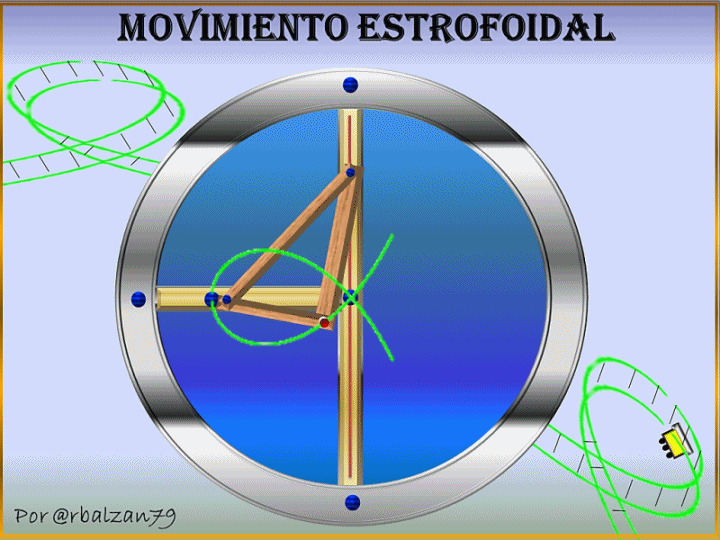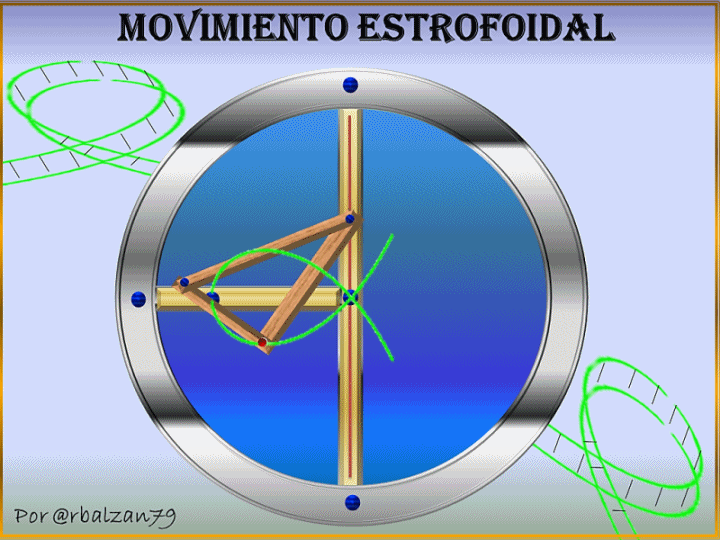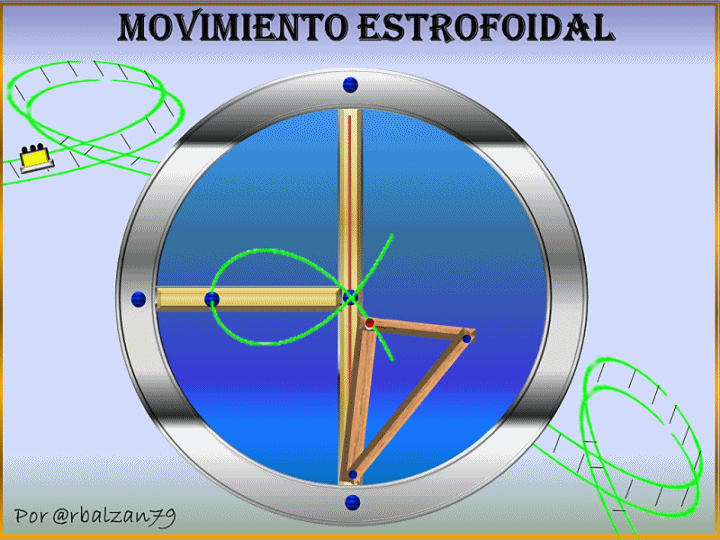
Es impresionante poder observar cualquier tipo de trayectoria recorrida por un móvil ya que toda curva nos permite profundizar en el aspecto cinemático del mismo, la curva estrofoide es una de esas espectaculares curvas que se encuentra en la naturaleza y que además de hacer sus contribuciones geométricas es una hermosa curva utilizada en el diseño arquitectónico y soñada por cualquier de nosotros para ser transitada como lo podemos observar en el gif al inicio de este artículo.

Nuestra geometría analítica nos permite seguir dotando de formas y figuras al mundo de la ciencia con esos impresionantes lugares geométricos por donde transita cualquier partícula, cuerpo u objeto (móvil) al llevar a cabo un determinado movimiento, vital aspecto que hemos comprobado en cada uno de las anteriores publicaciones y hasta este punto hemos transitado o recorrido grandiosas trayectorias las cuales se encuentran asociadas a reconocidas figuras geométricas como lo son: la línea recta, la circunferencia, la parábola, la elipse, la hipérbola, combinaciones de ellas así como alguno de sus fragmentos, descubriendo otras figuras muy complejas como la mariposa o atractor de Lorentz, curvas periódicas o armónicas, las cicloides, epicicloides, hipocicloides, la cisoide, representando cada una de estas figuras un movimiento tanto individual como combinado o complejo.

Para referirnos al lugar geométrico de la estrofoide utilizaremos la siguiente figura 1, en donde una determinada circunferencia de centro C y radio CA, donde delinearemos por el punto (C) una recta KL y esta forma un ángulo β con el radio antes descrito, localizamos un punto D entre el arco AK1 y desde allí trazamos una línea recta hasta O, generando el segmento o recta OD y la misma con posición variable, luego de dicha recta OD extraemos un segmento ON y este último deberá ser igual a la longitud ED, cuando la recta de posición variables, es decir, OD se mueva tendremos que el punto N va adquiriendo posiciones diferentes dibujando de esta forma el extraordinario lugar geométrico de la estrofoide como podemos notar a continuación:

En la anterior figura 1 podemos ver la formación de una estrofoide oblicua apoyándonos en importantes figuras geométricas como la línea recta y circunferencia, las cuales además de poder generar sus propios movimientos también contribuyen a la generación de curvas trayectorias para otros tipos de movilidades.

Ahora mostraremos la implementación del fenómeno del movimiento inyectados a dos puntos N1 y N2 pertenecientes a una recta que pasa por A, en donde P es un punto seleccionado arbitrariamente del eje OX, por lo tanto tenemos las siguientes igualdades de segmentos PM1=PM2=OP en un determinado plano generando una estrofoide recta, observando en el siguiente gif animado las distintas posiciones que toman los puntos N1 y N2 lo cual le permite a dichos puntos poder establecer el lugar geométrico de dicha curva estrofoide recta como se muestra en el siguiente gif:

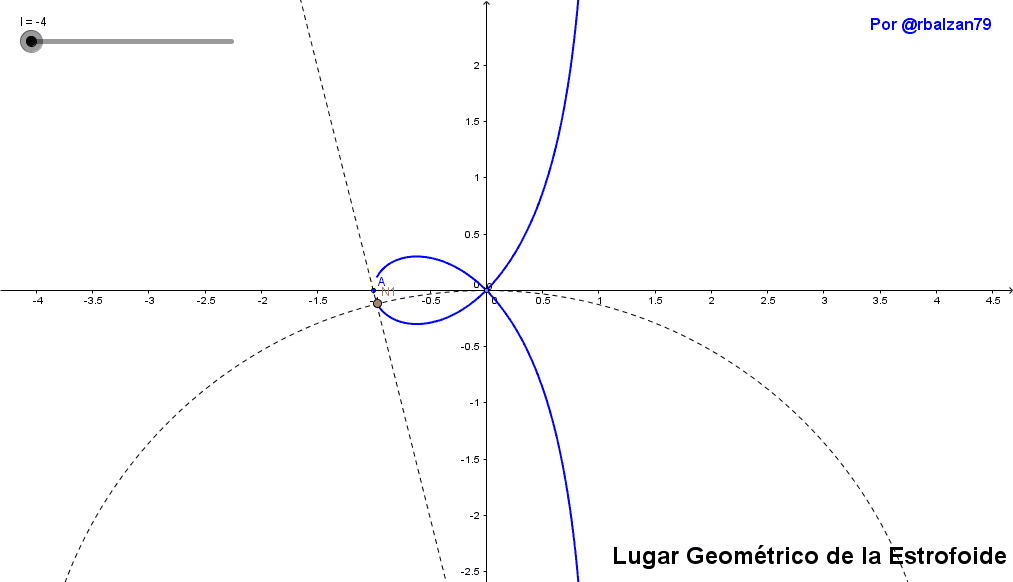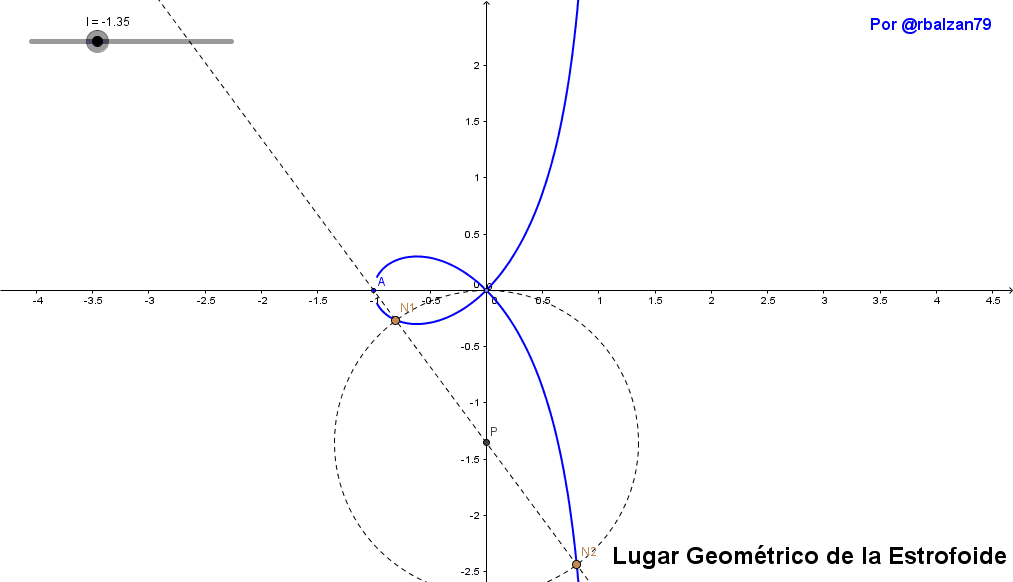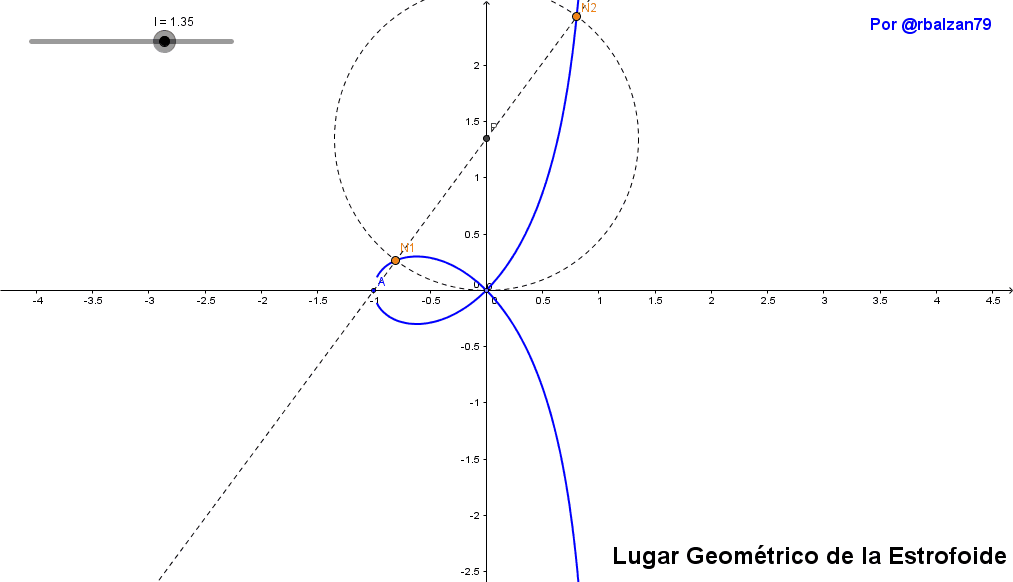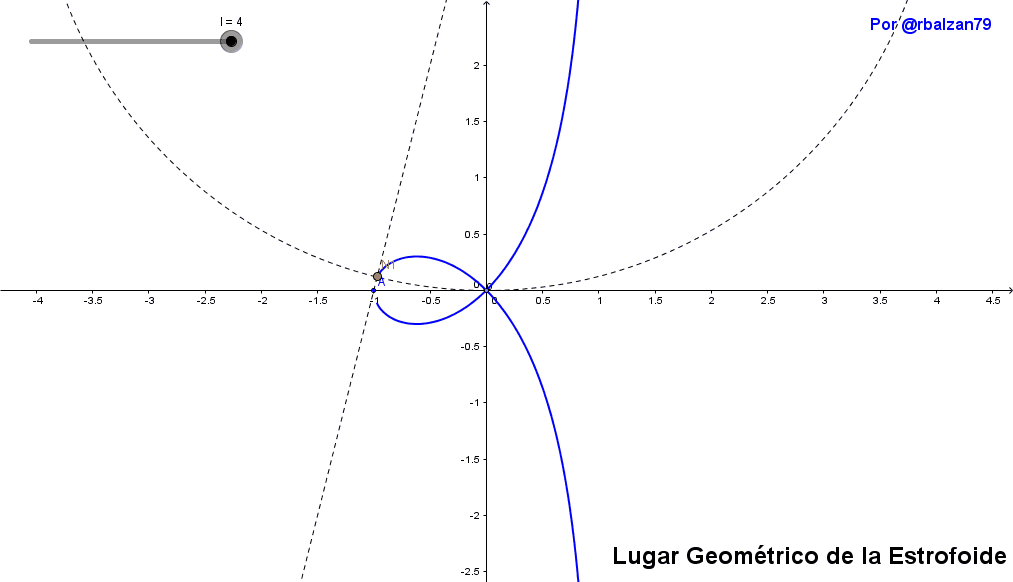
Al poderle brindar movilidad a un determinado punto nos permite poder visualizar de mejor forma las posiciones que toma tal punto al momento de dibujar cualquier figura como lo pudimos notar y comprobar con la movilidad de los puntos N1 y N2, y el cual como ya se ha expresado traza la forma geométrica de la estrofoide, por tanto mediante la unión de otras figuras (línea recta y circunferencia) podemos obtener nuevas curvas que a su vez estarían formando parte de la selecta lista para un particular movimiento que en este caso lo hemos denominado estrofoidal.

Recordando que para el fabuloso fenómeno del movimiento es imprescindible poder señalar la posición de cualquier partícula, cuerpo u objeto cuando transita por nuestro universo, en pocas palabras debe existir u originarse un cambio de posición del móvil pero además es también esencial distinguir la forma de la trayectoria seguida para de esta manera establecer cual es el tipo de movimiento que queremos analizar, es decir, acudir a la geometría analítica y cinemática como ya lo hemos hecho y con ello profundizado en distintos movimientos presentes en nuestras vidas como es el caso del movimiento analizado en este artículo, el estrofoidal.

# ***Movimiento estrofoidal***

Seguimos localizando diferentes tipos de movimientos desarrollados en nuestro imponente entorno y los mismos extraídos de lo natural para nuestro beneficio, cuando diseñamos cualquier curva a través de la geometría analítica y su ejemplar lenguaje algebraico nos permite hacer volar nuestra imaginación para luego plasmarlo en la realidad de forma o manera generalizada.

Quién de nosotros no ha transitado por una trayectoria en forma de línea recta o circular o ha visto recorrer cualquier cuerpo por increíbles lugares geométricos, esto nos hace dependiente del fenómeno del movimiento tal y como lo pudimos notar al momento de la estructuración de la curva estrofoide, de esa forma actúa entre nosotros cualquier rasgo de movilidad ya que genera la vitalidad necesaria para seguir existiendo en este hermoso y complejo universo.

Para describir el movimiento estrofoidal es preciso referirnos a la creación de la trayectoria que caracteriza dicho movimiento, es decir, la curva estrofoidal, ya que la misma se origina gracias a la geometría que denominamos cinemática, y es así, debido a que de la misma forma como se comporta el punto que traza esta curva podríamos decir que se podría comportar cualquier cuerpo o móvil al recorrerla, de nuestro espacio podemos concebir toda forma pero a través de la geometría cinemática ordenamos nuestras ideas plasmándolas en cada curva que nos conducirá a un determinado movimiento como lo es el estrofoidal.

La humanidad ha dado gigantescos saltos de evolución a medida que comprende cada vez más al fenómeno del movimiento y esto se evidencia a través de excepcionales sistemas físicos con mecanismos articulados para la transmisión de distintas formas de movimientos, en donde un punto cualesquiera de un determinado sistema puede desarrollar el movimiento estrofoidal como podemos observar en el gif al inicio de esta publicación o como también se observa a un móvil transitar por esta espectacular curva, en donde dicho móvil experimenta constantes cambios en cuanto a su posición derivándose de esta forma en una velocidad que por ser una curva es angular y también dándose por lo general por la forma de la curva periodos de aceleraciones, es decir, cambios en la velocidad del móvil.

Es lo impresionante del nexo de la geometría analítica y la cinemática ya que nos brindan además de extraordinarios conocimientos, también nos permiten hacer diversión con cualquier tipo de movilidad a través de distintas curvas, y en el campo de la enseñanza así como del disfrute en el transitar de cualquier curva la física es un gran ejemplo a seguir por sus valiosos aportes, claro a través de su cinemática y su nexo con la geometría analítica, como ya lo expresamos la geometría cinemática.

Por lo tanto seguimos afirmando que cualquier tipo de figura geométrica además de conservar características intrínsecas de movilidad de acuerdo a su formación o creación, y el cual lo hace dependiente de una forma de movimiento ya sea de uno o varios puntos de un determinado plano, reafirmando también que estas figuras siempre serán vitales en el desarrollo de cualquier fenómeno de movilidad presente entre nosotros bien sea como lugar geométrico (curvas), como trayectorias para un movimiento o como estructuras (por ejemplo, tipos de engranajes) para la transmisión de varias formas de movilidad.

En nuestro universo se desarrollan infinitos fenómenos los cuales el extraordinario campo de la ciencia ha tratado de entender cada vez mejor, y claramente esto lo ha ido consolidando a través de la implementación de los imprescindibles modelos matemáticos convertidos en las herramientas esenciales para que la humanidad se acerque aún más al entendimiento de nuestro muy complejo entorno natural, entonces dichos modelos constituyen la excelente personificación abstracta de dichos fenómenos naturales ya que nos permiten poder obtener de manera general o universal una comprensión acerca de un determinado planteamiento relacionado a cualquier situación de nuestro entorno y que además nos permita la resolución de futuros problemas de igual índole.

Cualquier rama científica se ha podido consolidar gracias a la debida comprensión algebraica o abstracta de las diferentes curvas aportadas por la geometría analítica, tanto estas figuras como sus formulaciones nos han permitido crecer en cualquier ámbito de nuestras vidas y a través del análisis de fenómeno del movimiento se ha probado dicha aplicación.

La estrofoide perteneciente a la familia cisoidal podemos decir que es aquella curva conformada por dos ramas proporcionales y sobre estas una curva en forma de una gota o pétalo, el nombre con el cual se conoce hoy día se lo colocó Montucci por 1846 y cuyo significado es correa enrollada, sin embargo, nuestros ojos pudieran expresar cualquier otra parecido tal vez con la de un molusco, lo cierto que es una hermosa figura implementada en muchas áreas de nuestro desarrollo intelectual, de la misma forma que las innumerables curvas conocidas por todos nosotros la estrofoide se generalizó a través de formulaciones matemáticas tales como las que tenemos a continuación:

Reafirmamos cada vez más que los maravillosos modelos matemáticos nos han permitido poder reducir notablemente el grado de complejidad que contienen cada uno de los excepcionales fenómenos naturales, logrando de esta forma que tanto la ciencia como cualquier persona de este planeta pueda entender de manera generalizada dichos fenómenos, claro esto requiere de mucho esfuerzo y constancia tal y como lo ha realizado el campo científico.

El movimiento nos ha dado todo lo que hoy tenemos, eso hace que nos topemos con el en todas partes y que además seamos necesariamente dependiente del mismo, todo lo que transcurre a nuestro alrededor se mueve de una u otra manera bien sea por aspectos cinemáticos propios a por estar sobre otra cuerpo, objeto o superficie que tiene movilidad o por el movimiento interno de sus moléculas, y de esa forma transcurre nuestro día a día, lo cierto es que sin darnos cuenta ocurren maravillosos movimientos mientras tratamos de entender algunos otros fenómenos naturales.

Cuando nos referimos a la geometría pensamos en cualquier figura o forma, sin embargo, por lo general obviamos el tipo de movimiento que se debe implementar para la creación de tales figuras como las diferentes curvas conocidas por todos nosotros, por lo tanto cuando analizamos un determinado movimiento nos enfocamos en aquel fenómeno desarrollado por cualquier partícula, cuerpo u objeto (móvil) al transitar o recorrer aquel espacio imaginario o físico el cual describe una trayectoria y que representa el lugar geométrico de una curva o figura.

Esto nos permite acotar que el entendimiento sobre cualquier tipo de movimiento parte desde el mismo instante que se elabora o dibuja una particular curva o figura y que luego se convierte en un complemento para el análisis o estudio de la movilidad de cualquier objeto sobre estas creaciones geométricas, es decir, se produce una consolidación entre los aspectos geométricos y cinemáticos de un movimiento, tal y como lo expresamos con la creación de la hermosa curva de la estrofoide y que al transitarla una determinada partícula, cuerpo u objeto desarrollará un movimiento semejante al punto del plano que la generó, es decir, el estrofoidal, tal y como lo pudimos observar en el gif animado sobre el lugar geométrico de la estrofoide.

Para concluir mis apreciados lectores hemos conocido otro tipo de movimiento el estrofoidal caracterizado por la implementación del lugar geométrico de la curva estrofoide, una impresionante curva utilizada en distintas áreas de las matemáticas como en otras importantes áreas como la arquitectura y por supuesto por la espectacular ciencia física a través de la cinemática generando el esencial nexo con la geometría analítica denominado geometría cinemática.

Hasta otra oportunidad mis apreciados lectores de steemit, en especial a los miembros de la gran comunidad de #STEM-Espanol, los cuales reciben el apoyo de otras tres grandes comunidades como los son #steemstem, #utopian-io y #curie, por lo cual recomiendo ampliamente formar parte de este hermoso proyecto, ya que resalta la valiosa labor de la academia y del campo científico, pero sobre todo, por el gran respecto, dedicación y ayuda para sus miembros.

Nota: Todas las imágenes fueron elaboradas usando las aplicaciones Paint, Power Point, el gif de la curva estrofoide fue realizada con GeoGebra y el gif animado al principio de la publicación fue elaborado con la aplicación de PhotoScape.

[1] Charles H. Lehmann. Geometría Analítica. Décima tercera reimpresión. Editorial Limusa. México, D.F. 1989.

[2] Jennings, G.A. Geometría moderna con aplicaciones. Springer, New York, 1994.

[3] Snapper, E., Troyer, R.J. Geometría afín métrica. Dover, New York, 1971.

[4] Raymod A. Serway y John W. Jewett, Jr. Ed. Thomson. Física. Edición 1 y 3. [5] Giancoli, D.C. Física, principios y aplicaciones, Reverté S.A. España, 1985.

[6] Mataix, M. La duplicación del cubo. Historias de matemáticos y algunos problemas. Barcelona, 1986.

[7] Arriagada Sandoval Camila. Modelos Matemáticos. Universidad del BÍO-BÍO. Chillan, 2015.

[8] Olalquiaga Pablo, Olalquiaga Alfonzo. El libro de las curvas. Fundación Esteico. 1era edición, Diciembre 2005.

[9] Lafuente J. Geometría diferencial de curvas en el plano. Enero de 1998.