¡Hola, amigos de Steemit!
En este documento les enseñaré el procedimiento que llevé a cabo para diseñar un prototipo de Reloj Digital (RD) el cual muestra las horas y los minutos por medio de diodos emisores de luz (LED'S) dispuestos en forma de "display de 7 segmentos". El diseño se basa en la aplicación de la teoría del álgebra Booleana, fundamentalmente lo relativo a circuitos lógicos y circuitos secuenciales con Flip-Flop. Internamente el sistema se compone de un conjunto de bloques interconectados, como veremos más adelante, los cuales realizan funciones específicas y serán objeto de diseño en el desarrollo de este artículo; no obstante, para que ustedes tengan una idea preliminar del asunto, les muestro a continuación la vista frontal del prototipo que elaboré. Para facilitar su uso, el RD cuenta con un botón de encendido/apagado (on-off), un botón de reseteo (Reset) que lleva a cero las horas y los minutos, un par de botones para subir o bajar la hora, y un par de botones para subir y bajar los minutos. Vale señalar, sin ánimo de jactancia, que este diseño lo hice en mis ratos libres a mediado de la década de los 90's, cuando dictaba cátedra de "Sistemas Digitales" como docente contratado por la Universidad Santiago Mariño, ubicada en Barcelona, estado Anzoátegui/Venezuela; materia que, por cierto, aprobé con la máxima calificación (10 puntos) cuando estudiaba Ingeniería Eléctrica en la Universidad de Oriente (UDO).
VISTA FRONTAL DEL RELOJ DIGITAL
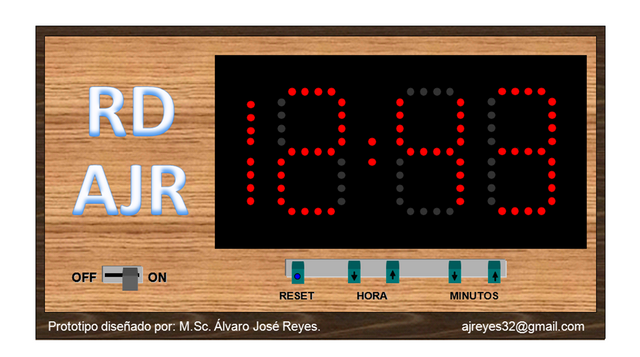
Autor: Álvaro Reyes
Ingeniero Electricista-CIV: 99.058
Cumaná-estado Sucre-Venezuela
Octubre de 2018
¡Sean todos bienvenidos!

El presente proyecto trata sobre el diseño de un Reloj Digital (RD) llevado a cabo por este humilde servidor. El diseño muestra la hora y los minutos a través de varios “display” de siete segmentos e indicará las pulsaciones de los segundos por medio de las señales luminosas emitidas por un par de diodos emisores de luz (LED’S). La Figura 1, muestra el diagrama de bloques (DDB) del reloj cuyo diseño les mostraré en este artículo. Como podemos observar, las partes que integran el DDB están claramente identificadas y cada una cumple una función específica. El diseño se basa en tomar la señal senoidal de corriente alterna (AC) cuya frecuencia es F = 60 Hz (60 ciclos por segundo) y transformarla electrónicamente en un tren de pulsos rectangulares de la misma frecuencia, es decir, 60 pulsaciones por segundo (60 pps), esto se lograría implementando un circuito “Configurador de pulsos” cuya salida, a su vez, alimentará a otro circuito denominado “contador MOD 60 entre 60” que divide la frecuencia del tren de pulsos y la convierte en 1 pulsación por segundo (1 pps). El bit menos significativo correspondiente al primer “contador BCD” lo utilicé para indicar con señal luminosa (LED'S) los pulsos de duración igual a 1 segundo. Vale decir que el funcionamiento del RD fue comprobado por medio de una simulación llevada a cabo con el software "MultiSim" obteniéndose un resultado correcto, basado en la selección de los componentes (circuitos integrados TTL) acordes a los requerimientos del sistema, los cuales están disponibles en la librería interna de "MultiSim"; no obstante, en la actualidad la implementación del prototipo en físico queda condicionada a la posibilidad de poder adquirir en el mercado tales componentes para el ensamblaje en un protoboard o para la construcción del mismo. Por lo pronto, dado el alcance de este artículo, lo que pretendo es mostrar los pasos que llevé a cabo en relación a toda la parte digital y secuencial del diseño, lo que de alguna manera podrá ser fácilmente asimilado por los amigos dedicados al ramo, sin descartar la comprensión por parte de quienes no conociendo la materia muestren interés en aprender sobre la misma.
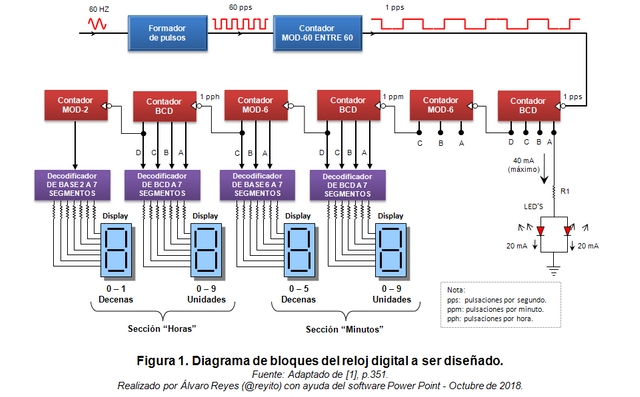
De acuerdo con lo anterior, se procede a continuación a diseñar los siguientes bloques que integran el Reloj Digital con base en la teoría del Álgebra Booleana y los Circuitos Secuenciales con Flip-Flop J-K:
- Contadortes BCD.
- Contadores MOD 6.
- Contador MOD 2.
- Decodificadores de BCD a 7 SEGMENTOS.
Nota: Se omite en en este artículo el diseño del "Formador de pulsos" porque corresponde a un circuito de electrónica analógica que bien pudiese ser explicado en detalles en otro post. Por lo tanto, nos centraremos en los bloques vinculados a la electrónica digital antes mencionados.

La ecuación de estado de un FF J-K tiene la siguiente forma:
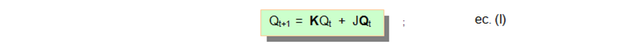
Donde:
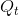 : estado actual del sistema.
: estado actual del sistema.
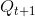 : estado futuro del sistema.
: estado futuro del sistema.
J, K: parámetros digitales a ser determinados a partir de la tabla de estados.
- Nota importante: las letras resaltadas con negrita en la ecuación de estado, representan el "valor negado" de la variable. Se observa en la ecuación anterior que aparecen los valores negados de "K" y "
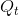 ".
".

De acuerdo con la Figura 1, el contador BCD dispone de 4 bits (D, C, B, A), siendo "A" el bit menos significativo y "D" el bit más significativo. Esta cantidad de bit's está relacionada con el número de Flip-Flop necesarios para implementar el contador BCD, como veremos a continuación.

La fórmula es sencilla:

Donde:
n = número de flip-flop.
Por lo tanto se requieren cuatro FF J-K (n=4):
- Flip flop A.
- Flip flop B.
- Flip flop C.
- Flip flop D.
El contador BCD deberá realizar un conteo cíclico secuencial desde el dígito “0” hasta el dígito “9” (es decir: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9); pero dado que no existe una potencia de base 2 cuyo resultado sea igual a 10 entonces será necesario inhibir los estados no permitidos correspondientes a los números: 10, 11, 12, 13, 14 y 15.

De lo anterior se deduce lo siguiente (véase la Figura 2):
- Estados permitidos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9.
- Estados no permitidos (inhibidos): 10, 11, 12, 13, 14 y 15.
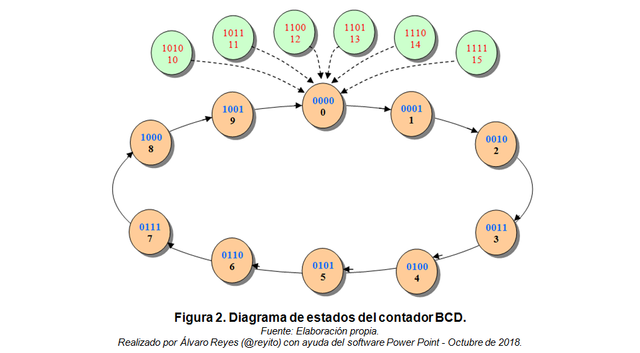

De la Figura 2, se obtiene:
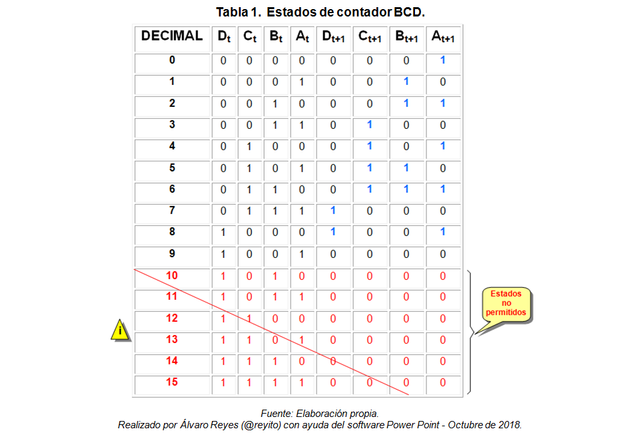

Partiendo de la tabla anterior y de la ecuación, se obtienen las ecuaciones de estado de los flip-flop: A, B, C y D.
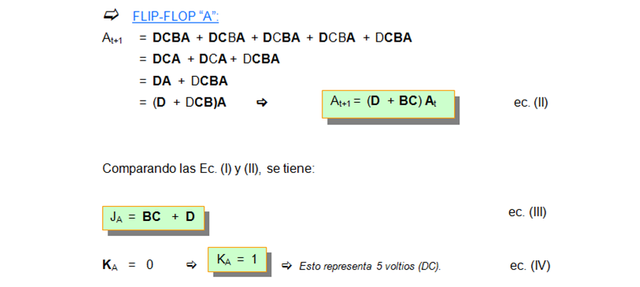
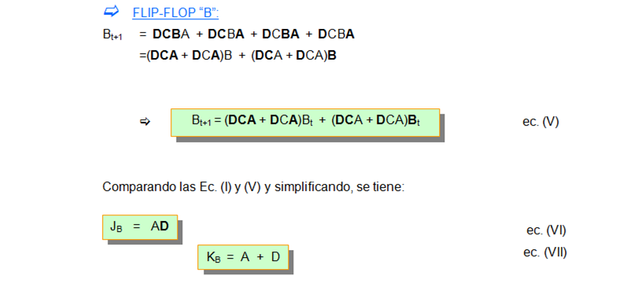
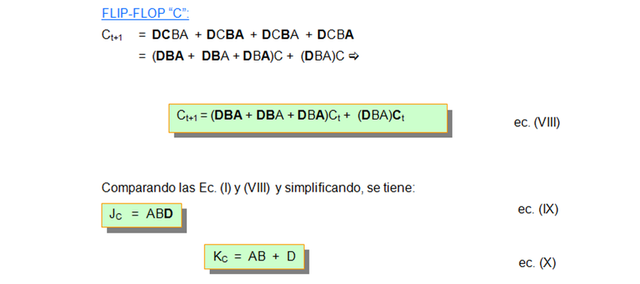

En resumen, se tiene lo siguiente:


El circuito lógico que se muestra a continuación se obtuvo a partir de las ecuaciones de estado indicadas en la Tabla 2.
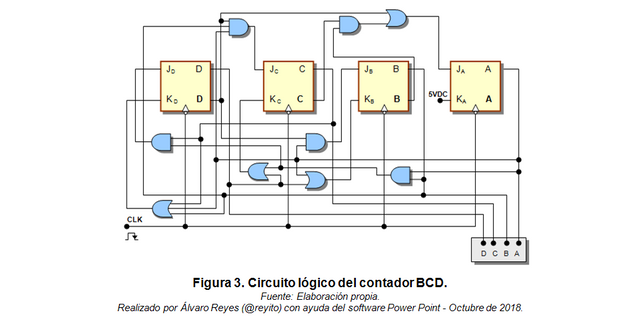
Observación:
- El circuito de la Figura 3, reemplazará a todos los contadores BCD de la Figura 1.

Se sigue un procedimiento similar al caso anterior. De acuerdo con la Figura 1, el contador MOD-6 dispone de 3 bits (C, B, A), siendo "A" el bit menos significativo y "C" el bit más significativo.

El contador MOD-6 realizará un conteo cíclico secuencial desde el dígito “0” hasta el dígito “5” (es decir: 0, 1, 2, 3, 4, 5); pero dado que no existe una potencia de base 2 cuyo resultado sea igual a 6 entonces será necesario inhibir los estados no permitidos correspondientes a los números: 6 y 7.
Por lo tanto se requieren tres FF J-K (n=3):
- Flip flop A.
- Flip flop B.
- Flip flop C.

De lo anterior se deduce lo siguiente (véase la Figura 4):
- Estados permitidos: 0, 1, 2, 3, 4 y 5.
- Estados no permitidos (inhibidos): 6 y 7.
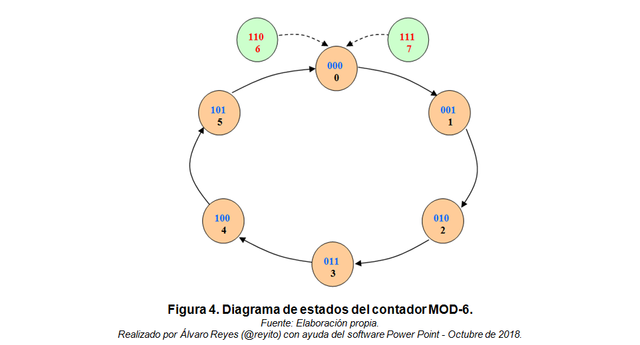

De la Figura 4, se obtiene:
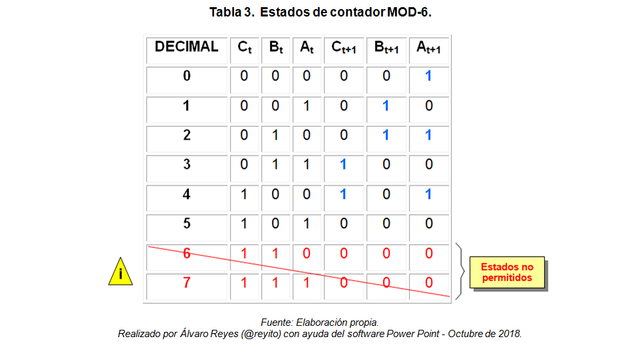

Partiendo de la ec (I), se obtienen las ecuaciones de estado de los flip-flop: A, B y C.
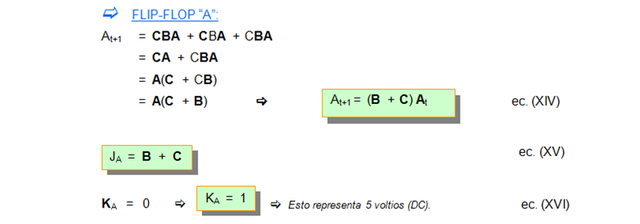

En resumen, se tiene lo siguiente:


El circuito lógico que se muestra a continuación se obtuvo a partir de las ecuaciones de estado indicadas en la Tabla 4.
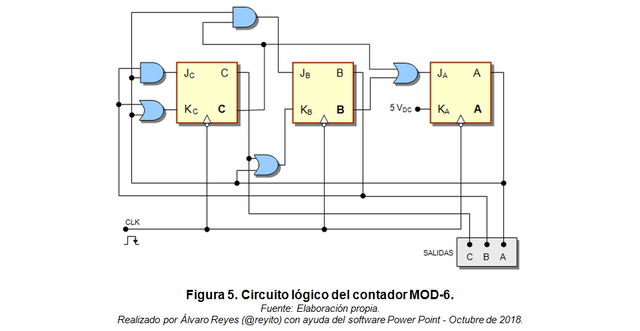
Observación:
- El circuito de la Figura 5, reemplazará a todos los contadores MOD-6 de la Figura 1.

De acuerdo con la Figura 1, el contador MOD-2 dispone de un solo bit; es decir el bit "A" cuyos valores pueden ser "0" ó "1".

El contador MOD-2 realizará un conteo cíclico secuencial desde el dígito “0” hasta el dígito “1” (es decir, en binario: 0 y 1).
Por lo tanto se requiere un FF J-K (n=1):

De lo anterior se deduce lo siguiente (véase la Figura 6):
- Estados permitidos: 0 y 1.
- Estados no permitidos (inhibidos): ninguno.
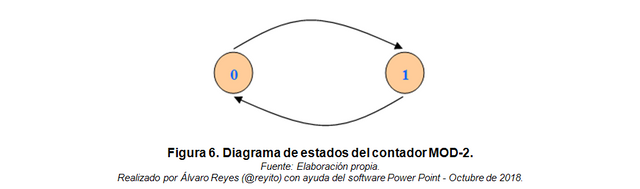

De la Figura 6, se obtiene:
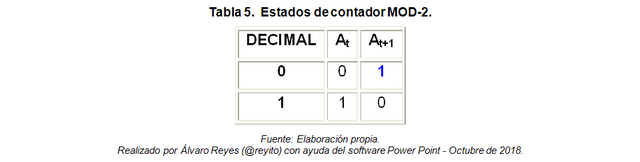

Partiendo de la ec (I), se obtienen las ecuaciones de estado del flip-flop A.


El circuito lógico que se muestra a continuación se obtuvo a partir del resultado anterior.
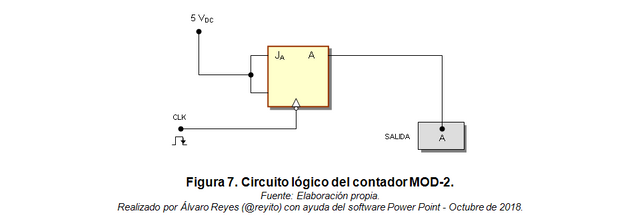

Observación:
- El circuito de la Figura 7, reemplazará al contador MOD-2 de la Figura 1.

Este decodificador tiene como función tomar la salida binaria de cuatro dígitos proveniente de un contador BCD para luego mostrarla a través de un grupo de LED’s dispuestos en configuración de “7-segmentos”.

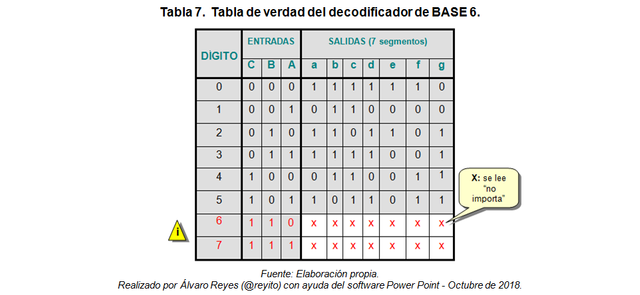
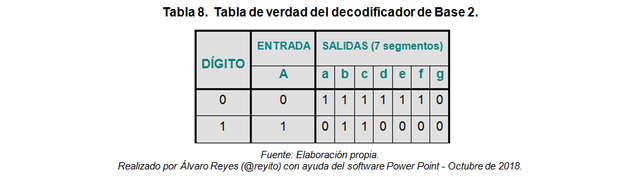
Sabemos que un contador BCD tiene 4-bit’s y por ende 16 estados posibles en código binario. Además, el conteo secuencial se realiza desde el dígito “0” hasta el dígito “9”. Por lo tanto, las entradas correspondientes a los dígitos “10”, “11”, “12”, “13”, “14” Y “15” no están permitidas. En el caso correspondiente a la sección “minutos”, éstos se cuentan desde “00” hasta el “59”; como se puede observar, el dígito menos significativo debe ser truncado para tal efecto. Luego, a partir de la tabla de verdad se procede a construir las ecuaciones lógicas correspondientes a cada uno de los 7-segmentos del display.

Es importante aclarar el significado de la “x” en la tabla anterior. Si partimos del hecho cierto de que el decodificador BCD/7S estará alimentado por la salida de un contador BCD, entonces por condición de diseño los estados correspondientes a los dígitos “10”, “11”, “12”, “13”, “14” y “15” están inhibidos ya que el contador automáticamente pasará del dígito “9” al dígito “0”. En otras palabras, el decodificador jamás recibirá los números binarios correspondientes a los dígitos “10”, “11”, “12”, “13”, “14” y “15”, por lo cual “no importa (x)” que se les tome en cuenta en la tabla de verdad. Los valores “x” tienen una gran ventaja en materia de diseño de sistemas digitales: permiten reducir el número de compuertas lógicas haciendo más eficiente y económico el circuito a implementar en la realidad.

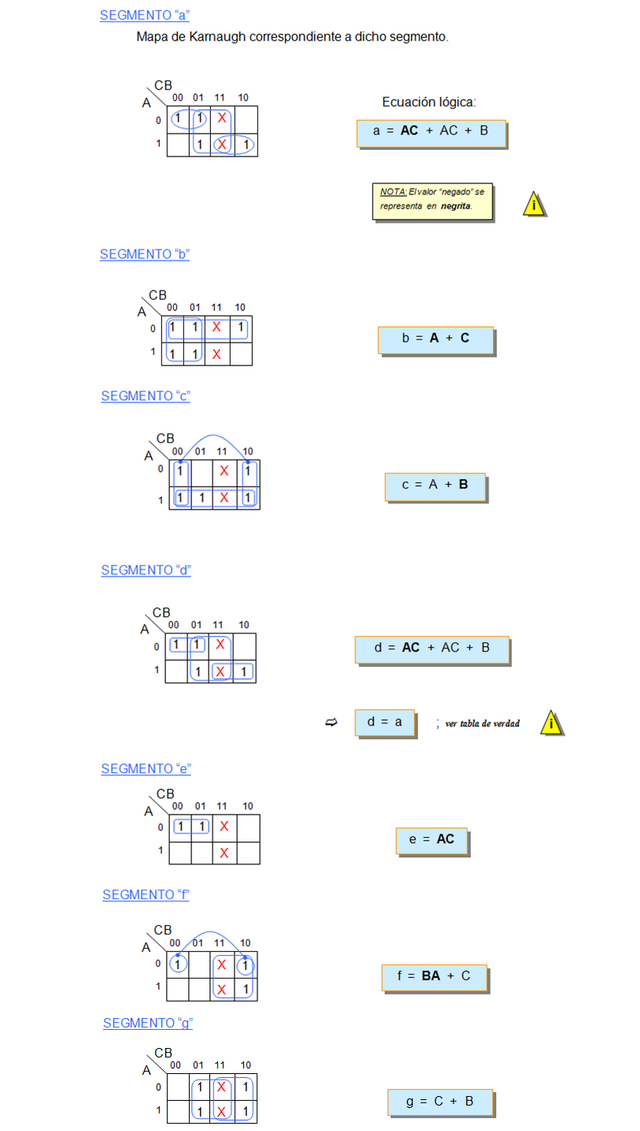
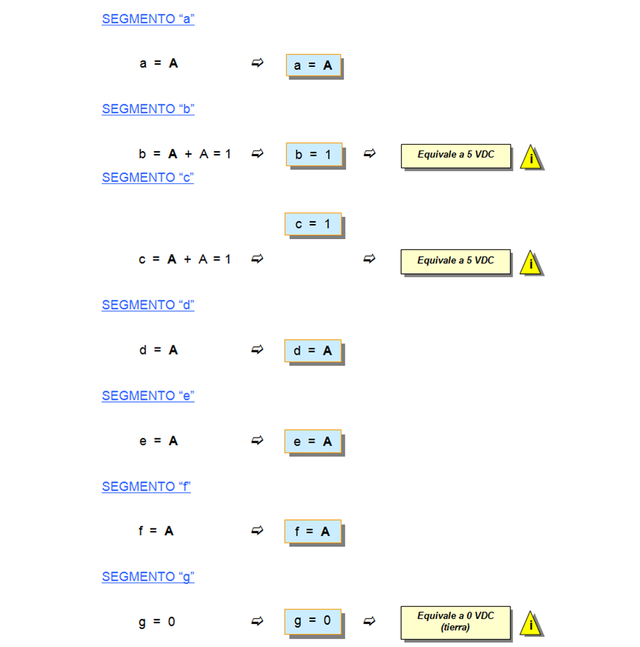
En el siguiente paso procedí a construir los mapas de Karnaugh (mapas K) correspondientes a cada segmento de display (segmentos: a, b, c, d, e y f), con la finalidad de reducir el número de compuertas lógicas y con ello simplificar las ecuaciones lógicas resultantes. De esta manera se logra obtener un circuito lógico más reducido en tamaño físico, más económico y eficiente.
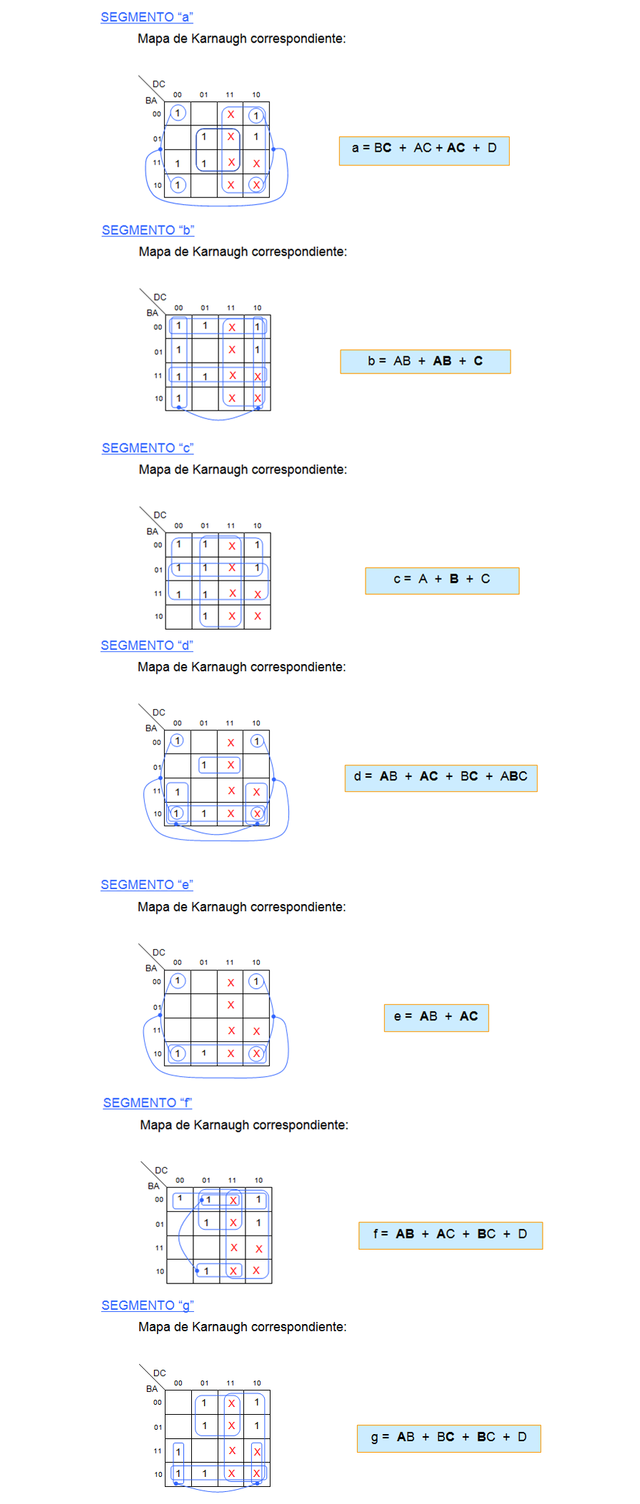

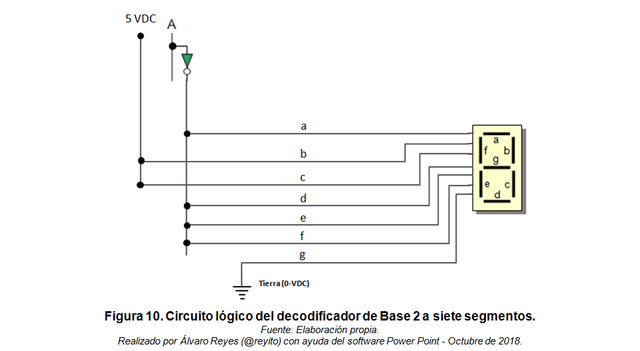
A continuación les muestro el circuito lógico que obtuve para el decodificador de BCD a 7 segmentos a partir del ensamblaje de las ecuaciones obtenidas con los mapas K.
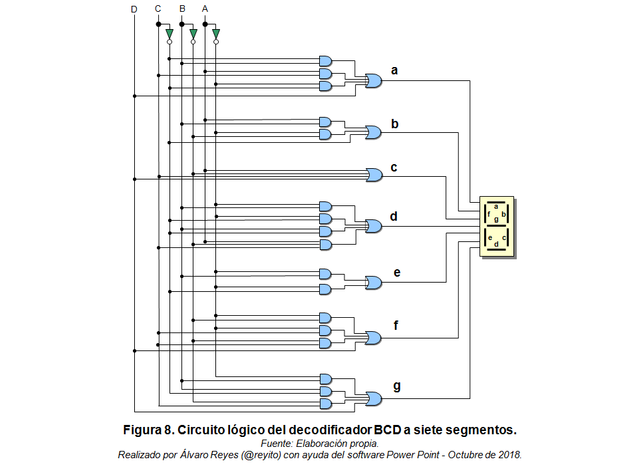

Este decodificador tiene como función tomar la salida binaria de tres dígitos proveniente de un contador MOD-6 para luego mostrarla a través de un grupo de LED’s dispuestos en configuración de “7-segmentos”. Para no hacer el documento muy extenso, procedo a mostrar los resultados.



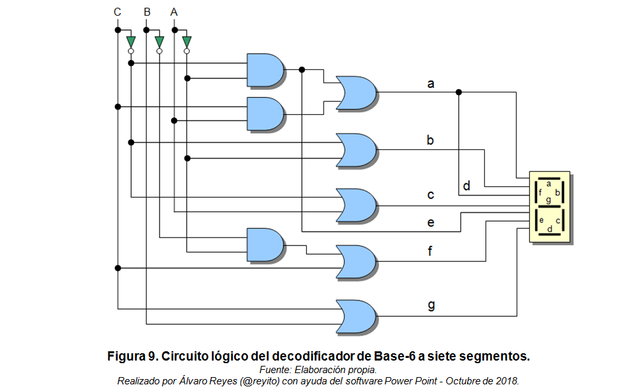

Este decodificador tiene como función tomar la salida binaria de un dígito proveniente del contador MOD-2 para luego mostrarla a través de un grupo de LED’s dispuestos en configuración de “7-segmentos”. Se procede en forma similar al caso anterior para no hacer el documento muy extenso.




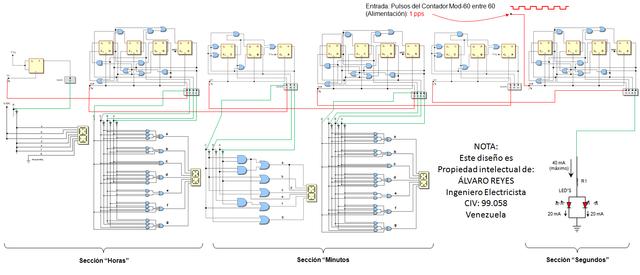
Para concluir, les muestro el ensamblaje a nivel circuital del diseño de prototipo de Reloj Digital desarrollado por este humilde servidor.


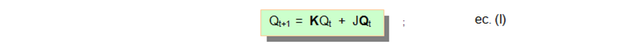
: estado actual del sistema.
: estado futuro del sistema.
".
































































Hola amigo @reyito, excelente tu diseño, felicitaciones por tan bonito proyecto, y el detalle con el que lo presentas. Me gusto mucho, he visto en mi trabajo muchos diseños parecidos, pero este me parece muy bueno.
Saludos cordiales.
Hola, @abdulmath, me alegra que te haya gustado mucho mi diseño. Gracias por tan bonito gesto. Te saluda un amigo en la distancia.
Hola @reyito, excelente aporte, se percibe la dedicación y el interés por mostrar detalladamente los saberes que nos compartes, te felicito, se nota tu dominio del tema!! Abrazos fraternos!!
Hola, @reinaseq. Quiero darte las gracias por leer y votar mi artículo. Por otro lado, me alegra mucho el contenido de tus palabras en especial cuando calificas mi artículo como "excelente aporte". En verdad te digo, las cosas hay que hacerlas con dedicación, entrega y mística, porque para eso fuimos formados como profesionales; estoy convencido de que eso marca la diferencia de lo común. Donde quiera que estés, recibe mil bendiciones.
Excelente artículo, profesor @Reyito. Me hizo recordar algunas cosas de mis estudios del pregrado, en especial por lo de las compuertas lógicas. Me gustaría saber si puede hacer un reloj de ajedrez 😄 Este dispositivo está compuesto por dos relojes. Cuando un de ellos comienza a funcionar, el otro inmediatamente se detiene, y viceversa. Ambos andan en cuenta regresiva porque la idea es que el primer jugador que consuma todo su tiempo, perderá la partida. Supongo que dado lo planteado aquí, no debería ser muy complicado diseñarlo. Saludos y éxito!
Hola, @eniolw, en primer lugar debo darte las gracias por comentar y votar este post y por calificarlo como excelente. En segundo lugar, permíteme decirte que sí se puede hacer el "Reloj de Ajedréz"; es más, me parece interesante desarrollarlo y mostrarlo en Steemit. ¡Para serte franco no había pensado en esa maravillosa idea! En tercer lugar, respecto al conteo regresivo que ambos relojes deberían realizar, es el punto clave para el desarrollo de las "tablas de estado" de los contadores. En fin, me encanta tu idea y es factible desarrollarla. Estamos en contacto.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Hi, @SteemSTEM. First of all, I want to thank SteemSTEM's healing team for voting my article. Second, I appreciate the work you are doing. For this reason, I have voted both projects per witness by selecting stem.witness and curie. Third, I have joined you in Discord. Thank you for making me part of that prestigious community.
Congratulations @reyito! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard: