Respuesta Escalón de un Sistema de Control Lineal con Realimentación Negativa Unitaria || Ejercicio

Hola, amigos de Steemit


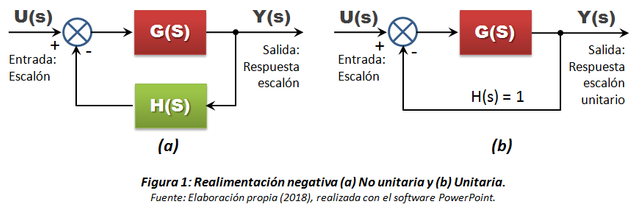


Iniciemos la solución de un ejercicio que nos permita visualizar de una manera más explícita lo que se busca como propósito en este documento.

Tomemos como ejemplo una Planta cuya función de transferencia está dada por:

Si sustituimos (II) en (I), se obtiene:

Para una señal de entrada tipo escalón: , la salida correspondiente en el dominio de Laplace, es:
Aplicamos expansión en fracciones parciales y obtenemos:
Finalmente, obtenemos la salida o respuesta del sistema en el dominio del tiempo aplicando la transformada inversa de Laplace:
Es decir:

La Figura 5.13(a) de [1] (p.255) corresponde a los porcentajes de sobreelongación en función de los valores ,
y "a" cuando la expresión de salida Y(s) tiene la forma:
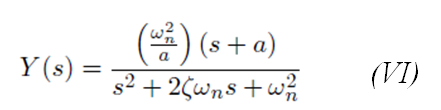
Tras analizar la función de transferencia encontrada en el inciso (a), podemos dar con los siguientes valores:
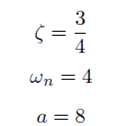
Con estos valores resulta posible efectuar el siguiente cálculo:
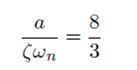
Y finalmente localizamos en la Figura 5.13(a) de [1] el porcentaje de sobreelongación correspondiente:

Aplicamos el teorema del valor final a (IV) para encontrar el valor de la salida en estado estable :
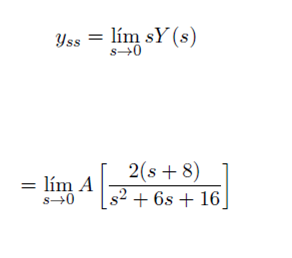
Por lo tanto:
En particular, para una señal de entrada de tipo "escalón unitario" , el valor ESTABLE de la salida es:

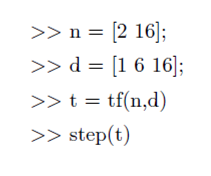
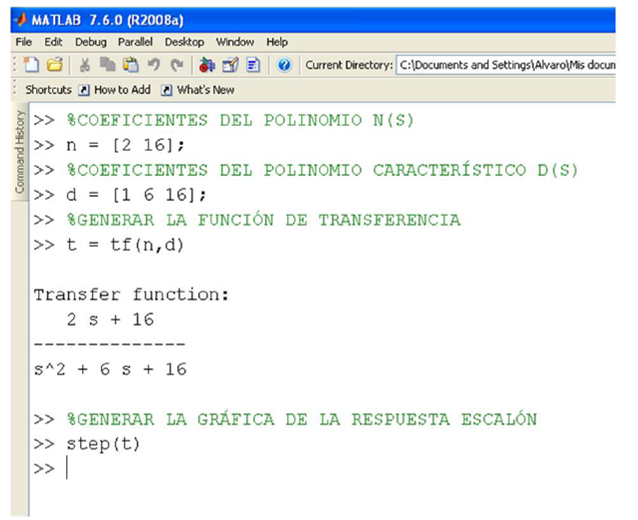

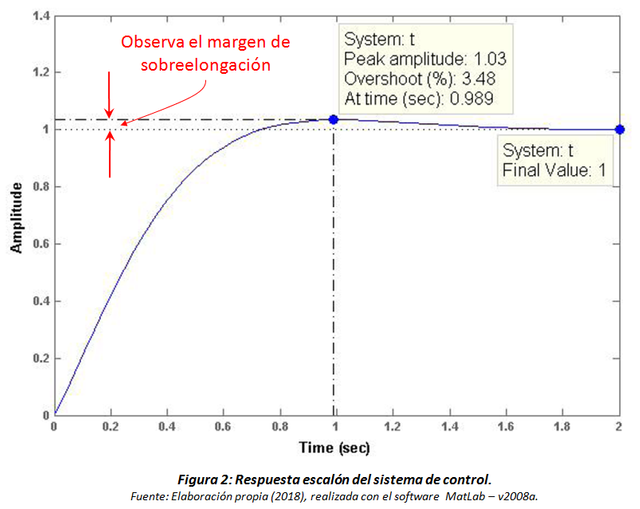
Véase la figura 2.

Los resultados obtenidos en este caso particular, permiten concluir lo siguiente:
- El sistema es invariante en el tiempo porque los coeficientes de la función de transferencia son constantes.
- El polinomio característico indica que se trata de un sistema lineal de segundo orden (n=2).
- La sobreelongación obtenida indica que la respuesta de salida del sistema sobrepasa en un 3.5% a la respuesta deseada.
- La salida alcanza la amplitud máxima de 1.03 unidades a los 0.989 segundos; instante correspondiente a la sobreelongación obtenida.
- Después de transcurrido el régimen transitorio, la señal de salida se estabiliza en su valor final (yss=A).
- Cuando la entrada corresponde a un escalón unitario, la salida se estabiliza en yss = 1.
- En la Figura 2, se observa que la respuesta del sistema es SUB-AMORTIGUADA, por lo tanto el sistema posee dos raíces complejas conjugadas estables (σ > 0).



Hola @Reyito. Espero estés bien. Revisa la etiqueta de español porque es #stem-espanol. Eso disminuye la visibilidad de tu post. Saludos.
Gracias, @eniolw, por leer y votar mi artículo; además por la sugerencia relativa a la etiqueta. Intentaré corregirla. También yo sigo tus publicaciones. Te saluda un amigo en la distancia.