Math that applies to our daily lives: The birthday problem/paradox
There are two types of friends in the world, those who celebrate you on your birthdays and those who expect you to celebrate them on your birthdays…yes that is a thing. Since evidence has shown that humans are inherently self-serving, I for one would prefer to be among the first group of friends, but if luck decides not to shine on me, I’d rather not be in there alone. Here’s why.
Where my preferred friend group would absolutely make me the sole focus of attention and all the good things that come with your birthday (…yes, I’m needy like that), I would rather not share that day with anyone else (yeah...roll your eyes, gasp all you want. I said what I said). Obvious reasons, I mean what should entirely be mine, I would have to you know…share it with you. Ugh!! There are other dates, pick one. Totally unfair!
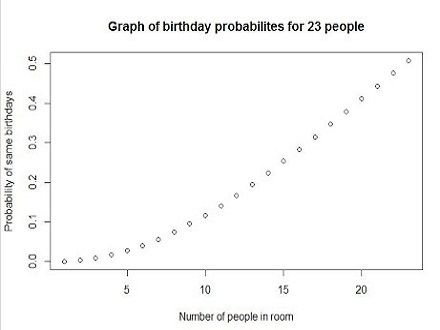
In a group of friends that would call you on your so called “special day” only to inquire about your plans for them, I would be more comfortable…scratch that, I’d gladly share that burden of responsibility to them with everyone else. I mean it’s obviously someone else’s birthday too, so I have to think of that, then I’m supposed to deal with you guys too. So much pressure (y’all don’t even care that much). It turns out that in a group of just 23 people the chances of two people having the same birthday is 50%. If that group increases to 75 there’s a 99.9% chance of two people matching. In a group of 366 people (the most number of days in a year), you are sure of getting two people with the same birthday so the probability is 100%.
How many friends do I have again?
To me this was a genuine problem, and I was super elated to find out that the good mathematicians who deemed it fit to make my growing up years miserable had a solution for my predicament, and called it “the birthday problem” (duh!!)
How it works
Solving the birthday problem, involves us using one of the basic rules of probability: the sum of the probability that an event will happen and the probability that the event won't happen is always 1. Meaning, the possibility that anything might or might not happen (total sum of all the outcomes) is always 100%. If we can work out the probability that no two people will have the same birthday, we can use this rule to find the probability that two people will share a birthday.
Since it’s easier to look at the probability that people do not share a birthday. Excluding February 29 birthdays (for simplicity), a person's birthday is one out of 365 possibilities. The probability that a person does not share the same birthday with another person is 364/365 because there are 364 days that are not a person's birthday.
This tells us that there is a 364/365, or 99.726027% of two random people not having matching birthdays.
Working out the probability that no one shares the same birthday in a group of 23 people
We should know that in a group of 23 people, there are 253 comparisons, or possible combinations, that can be made.
r!(n-r)
2!(23-2) = 235
Looking at 253 combinations, every single combination of the 253 has the same odds, 99.726027%, of not being a match. Multiplying 99.726027% by 99.726027, 253 times; or calculating (364/365)253, you'll get 0.49952. Which is a 49.952% chance that all 253 comparisons contain no matches. This implies that, the odds that there a birthday matches in the 253 comparisons is 1 – 49.952% = 50.048%.
Another way…
- The first person can be born on any day, so his probability is 365/365.
- The next person now has 364 possible days, so his probability is 364/365.
- The third person, has 363 days, so 363/365.
Continuing this pattern, the last persons probability would be of 343/365 (365 – 22 days since the persons took 22 potential days).
Multiplying all 23 probabilities together, would entail us writing out all the possible scenarios (365/365 × 364/365….343/365), but thankfully, they all share the same denominator, so we have 36523
Employing the use of factorials(!), to make it easy for us to multiply descending positive integers, 365! equals the product of all the descending integers from 365 down to 1. Since our group is 23 people large, we are only concerned with the product of the integers from 365 to 343, so we’ll take out the unnecessary by dividing 365! by 342!
365!/ 342! - 36523
This translates to 0.49952 or a 49.952% chance of no one in the group sharing the same birthday. To find the probability of two people having the same birthday, from the same group;
1 -0.49952 = 50.048
Yes, I am aware that life can throw you a curve ball by sending all people sharing your birthday to your group of friends…then again, it could not.Of course, it would be easier to walk up to people and ask them what day their birthdays were, but where’s the fun in that. Plus, you run the risk of sounding creepy or worse get found out. So,the next time you run into someone new…
365!/(365-n)!-(365n).
References
Image credits


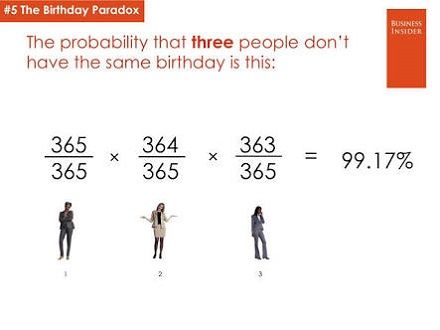
Being A SteemStem Member
Loool...all these stress does it really matter? Birthdays are birth days...you can decide to not do anything special...
Hehehe...Well, some people are interested in knowing the probability of others having the same birthday as them...